🤔 In Last Post
2d image를 가지고 3d를 예측할 때
- 사진 한 장으로는 정보가 부족했다.
- 2장 이상의 사진 사용
: data 사이의 관계 파악이 중요
- disparity image : 왼쪽을 기준으로 depth, 오늘쪽을 기준으로 depth로 2개의 depth를 얻을 수 있다.
→ 서로 다른 시점간의 관계 파악이 중요하다.
💭 what if…
남이 찍은 사진 2개로 stereo system을 사용하고 싶으면..?
→ 두 카메라 사이의 상호관계를 알아야 한다!!
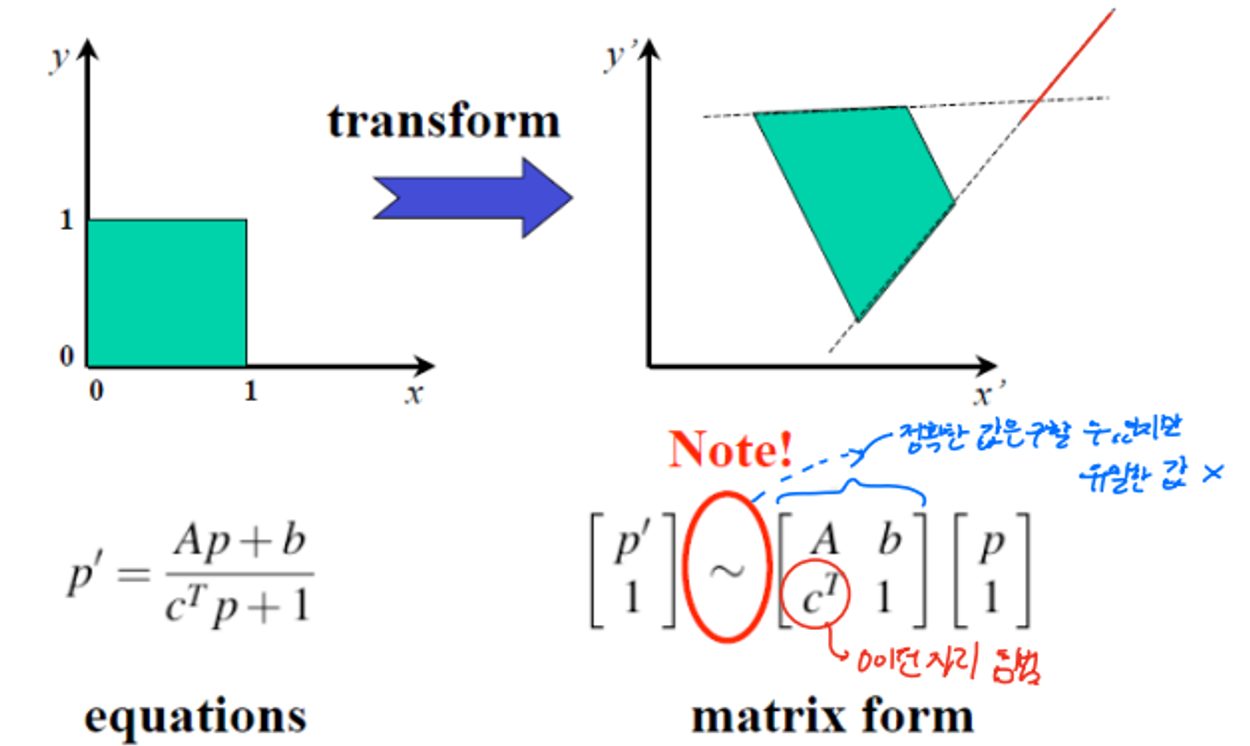
이번 장에서는 주어진 두 image 간의 transformation 관계를 찾고자 한다.
이전에 Stereo system에서는 dense하게 correspondence point를 찾았다면 이번에는 sparse(확실한) correspondence 를 찾는다. 그리고 이를 기준으로 하여 역으로 카메라 사이의 이동 관계를 알아내고자 한다.
📌 Image Mapping
✅ Geometric Image Mappings
기준이 되는 이미지와 transformed된 이미지 사이의 관계를 파악하고자 한다.
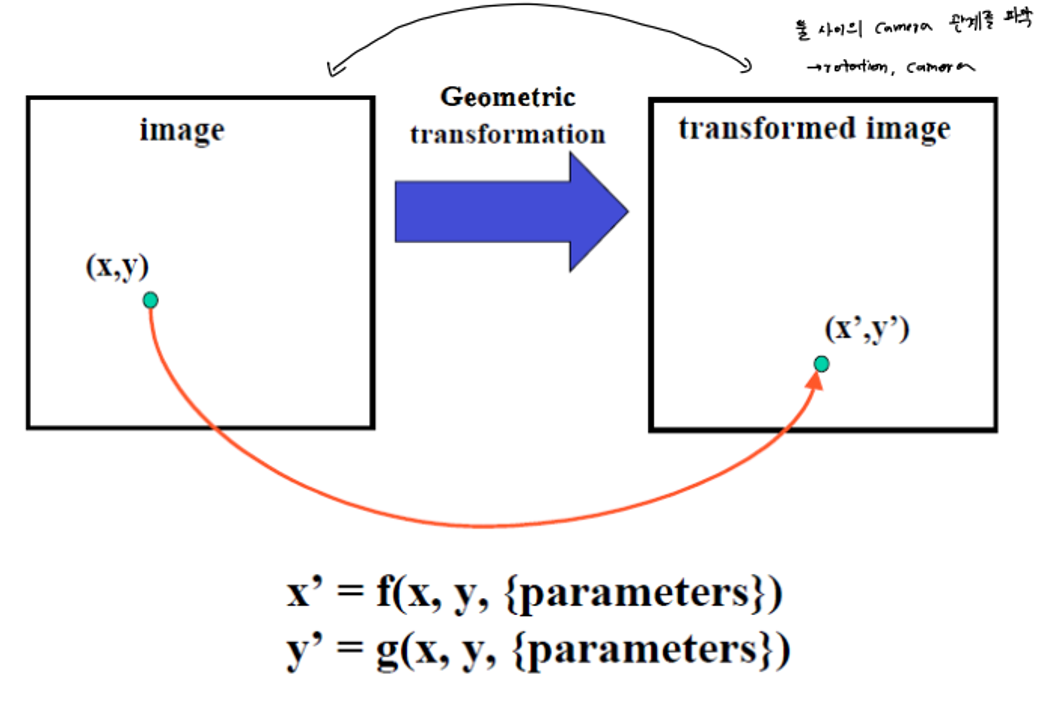
✔ Linear Transformation
- 관측 데이터 : [x’ y’ 1] 은 [x y 1]
- unknown : matrix M의 parameter
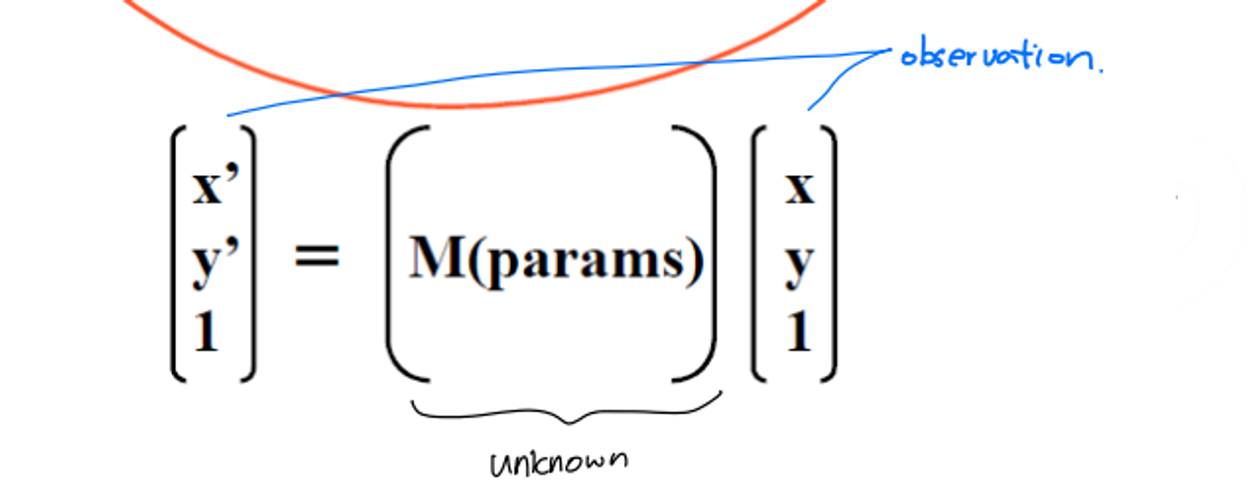
✅ Translation
✔ 2D
- translation matrix를 추정하기 위한 unknown parameter : 2개 (=dimension)
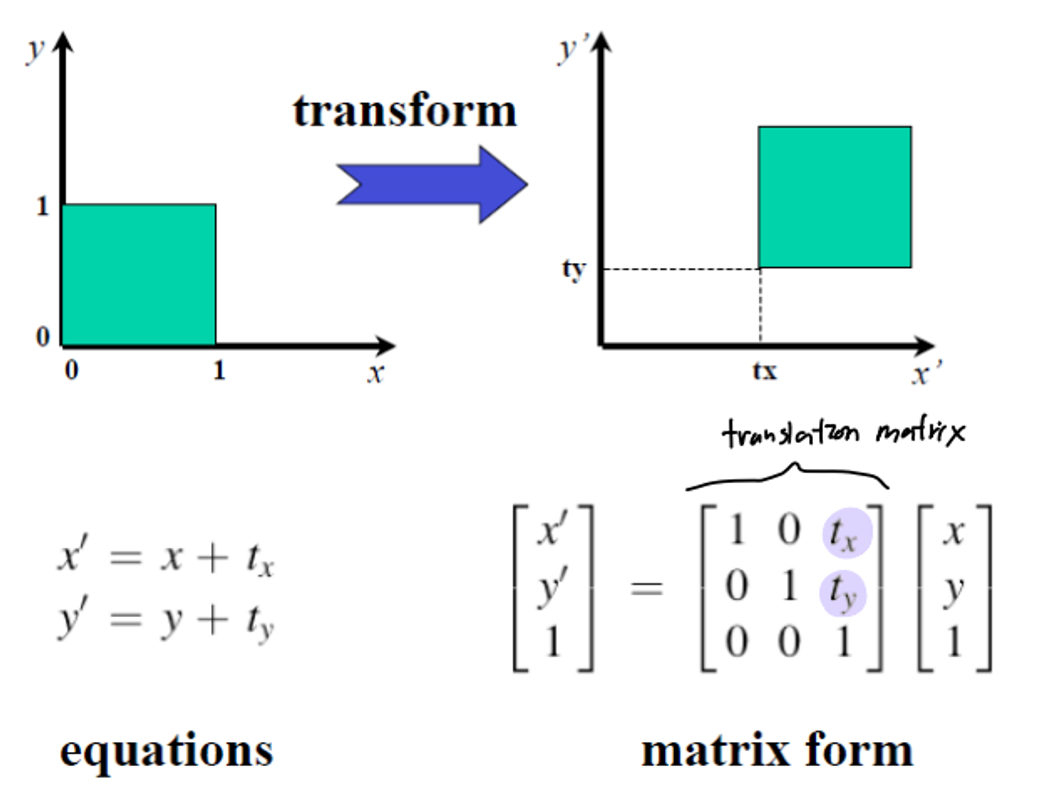
✅ Estimating a Transformation

✅ Example: Translation Estimation
이 예시에서는 translation 만 존재한다고 가정한다.
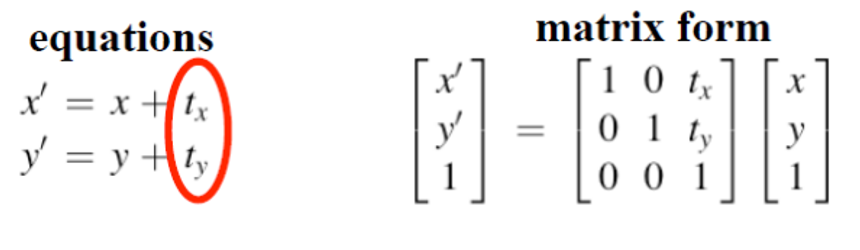
DoF=unknown parameter: 2- 필요한 최소
correspondences: 1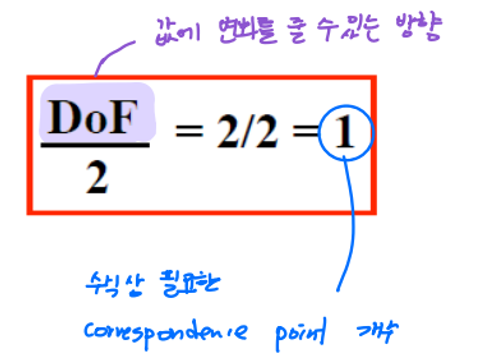
equation에서 볼 수 있듯 우리가 모르는 파라미터는 2개이다. 즉 corresponding point를 하나만 알아도 (이 하나가 pair로 되어 있으니) 파라미터를 구할 수 있다.
그러나 이건 이론적인 이야기이다. 현실은 여러 error가 존재하기 때문에 하나만으로 파라미터를 구하는 것은 좋지 않다. 아래 사진의 예시에서도 4개의 corresponding point 를 사용한다.
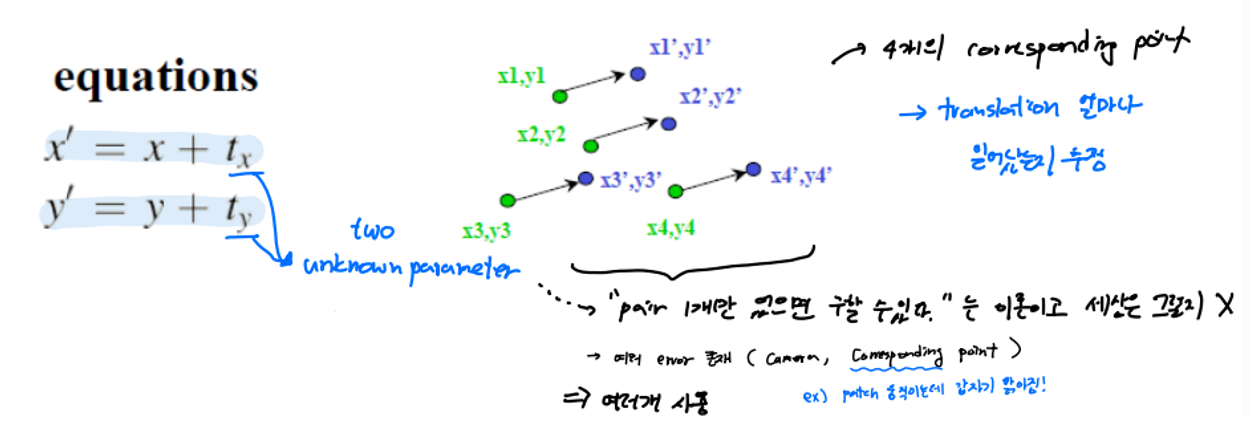
그렇다면 여러개의 corresponding point을 사용해 구할 때 에러를 최소화하기 위해 어떻게 할까?
→ Least Square estimation을 사용한다.
error = (이동전 값 + 추측한 이동값 파라미터) - 이동후 값 이 된다.
이 때 이 error 미분해 극값을 찾아 최소가 되는 를 구한다. → error를 최소로 만들어주는 translation 값

✅ Transformation Groups
아래 세 개의 조건을 만족하면 transformation group이라고 부른다. 이 transformation group 이 되면 property를 편하게 사용 가능해진다.
translation, rotation 모두 Transformation Groups에 속한다.

아래 사진처럼 우리는 손쉽게 inverse를 구할 수 있다.
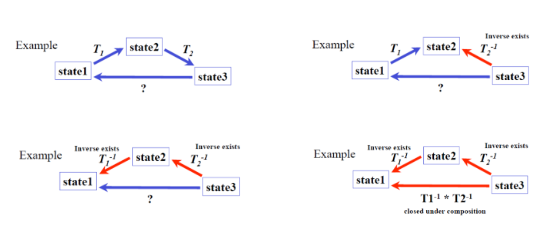
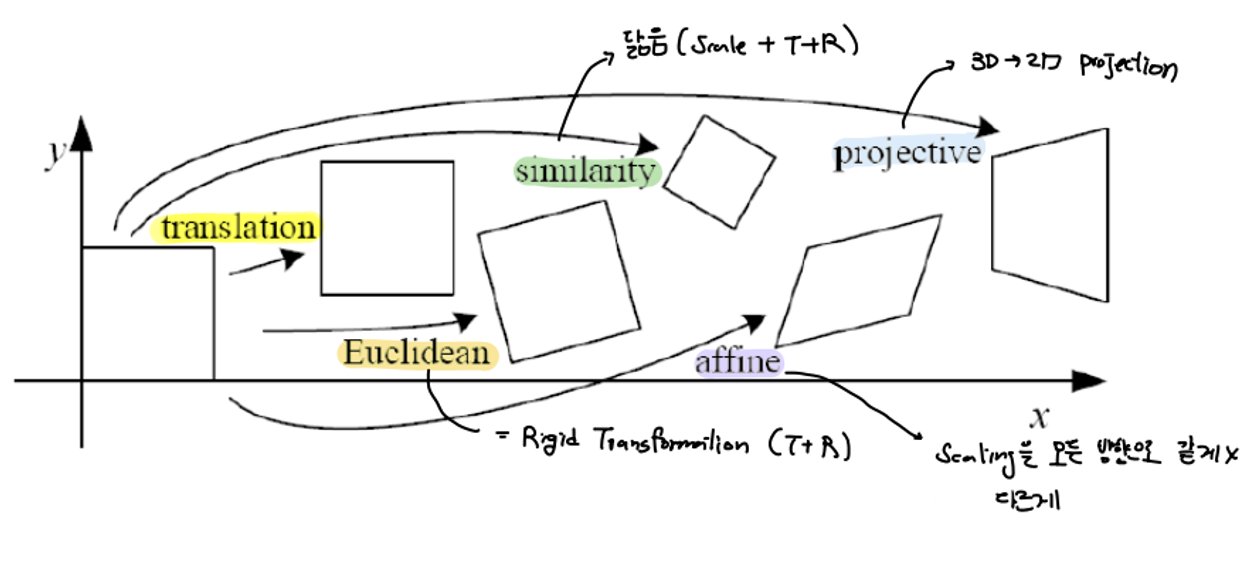
Basic set of 2D planar transformations
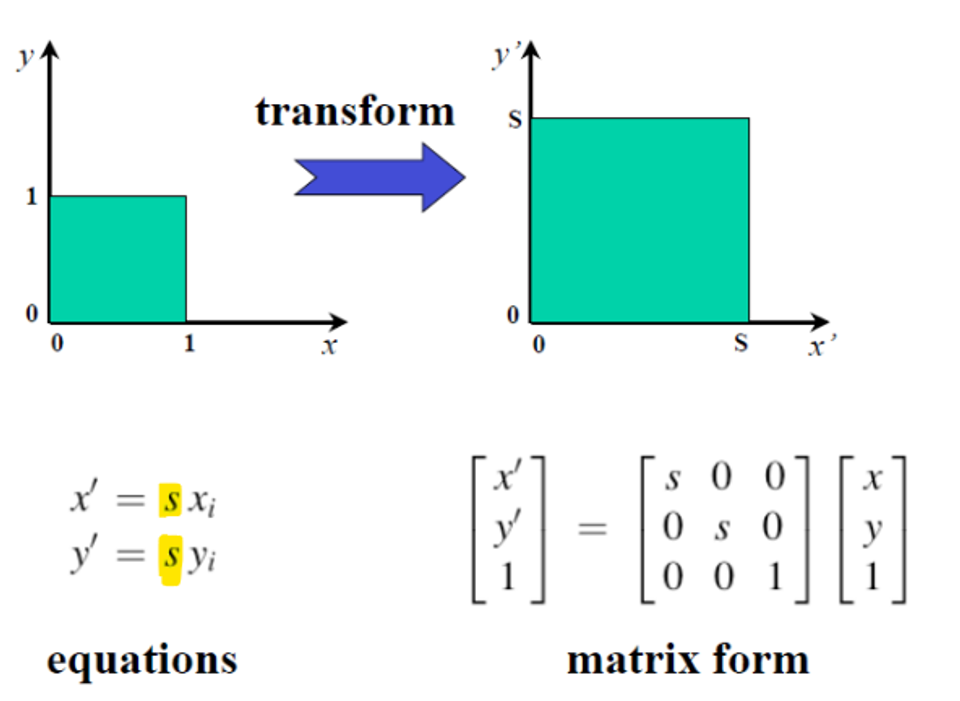
✅ Scale
2D
DoF=unknown parameter: 1 (one scaling factor)- 필요한 최소
corresponding point: 1
what if…
- s가 == 0
→ 사라진다.
- s가 음수
→ 반대로 켜진다.
- 상자가 원점에서 떨어져 있으면 어떨까?
→ 상자에 위치가 변한다.
따라서 이런 경우에는 먼저 원점으로 옮기고(Translation) Scaling Up 한 이후에 다시 Translation Back 해주어야 한다. 이때 back 해주는 과정은 위에서 transformation group에서 본 것 처럼 인버스로 간단한게 해줄 수 있다.
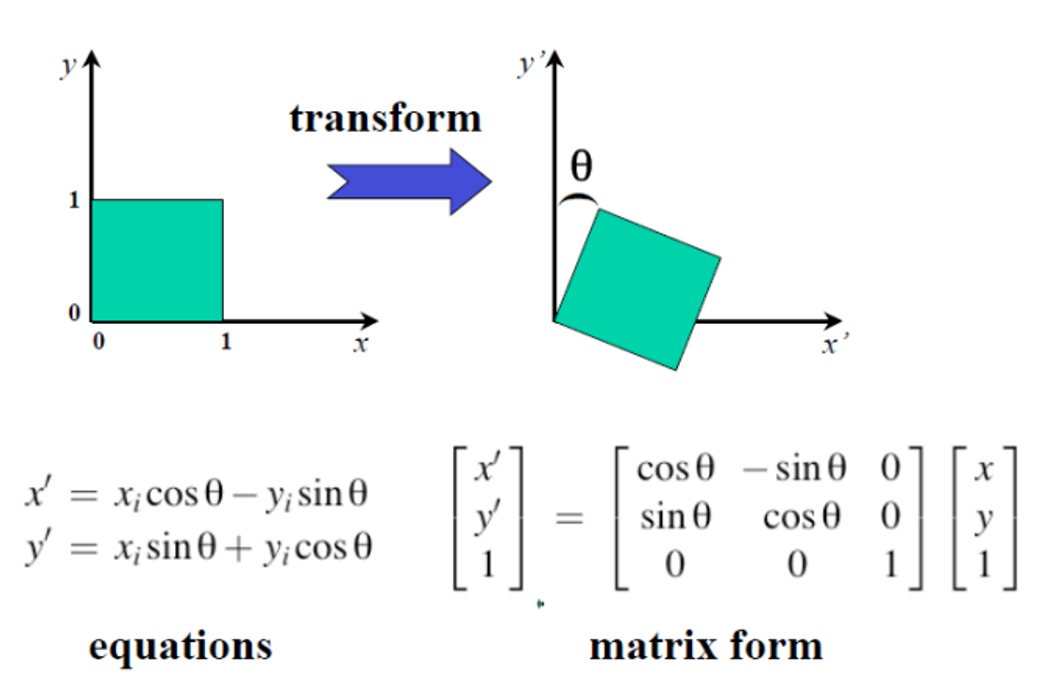
✅ Rotation
2D
DoF=unknown parameter: 1- 필요한 최소
corresponding point: 1
3D
Dof: 3
✅ Euclidean
= Rigid Transformation = Translation + Rotation
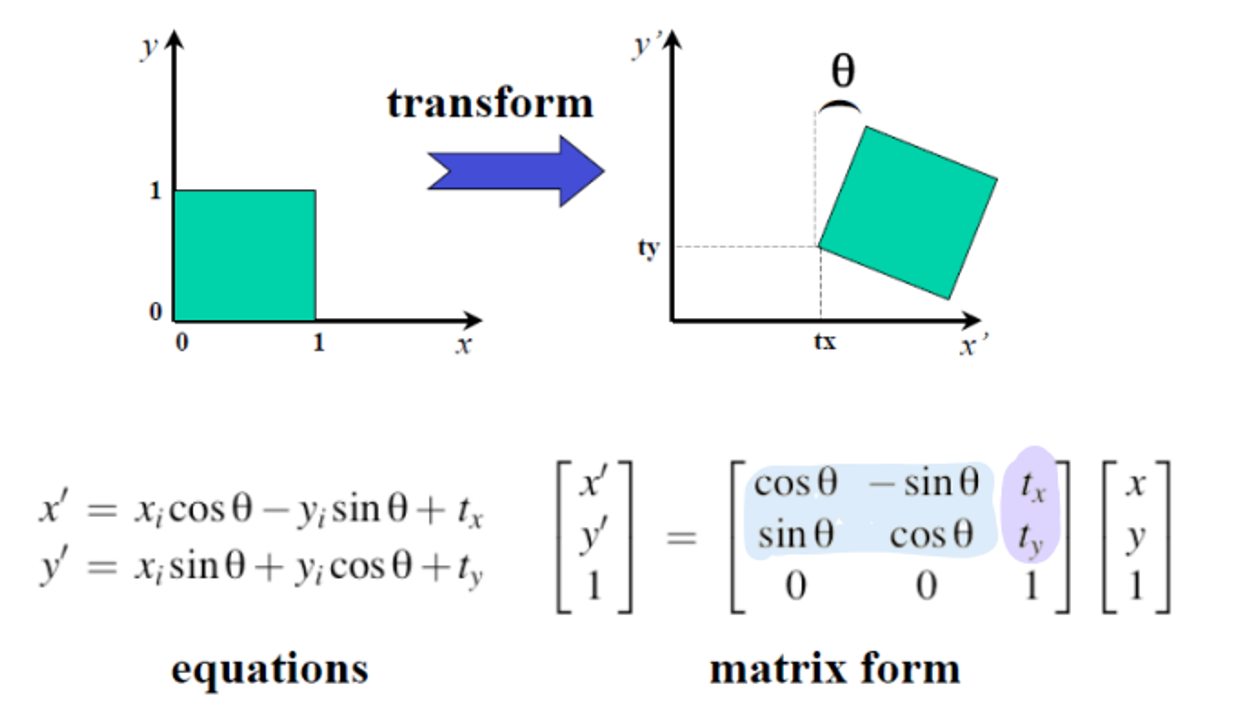
(Translation + Rotation) Matrix 를 아래처럼 표현하기도 한다.
R: rotation matrixt: translation
지금은 2차원이라 이걸 왜 이렇게 쓰나 굳이 라는 생각이 들 수 있는데 차원이 커질수록 매트릭스의 크기가 커지기 때문에 이런 식으로 쓰는게 더 간편해질 것이다.

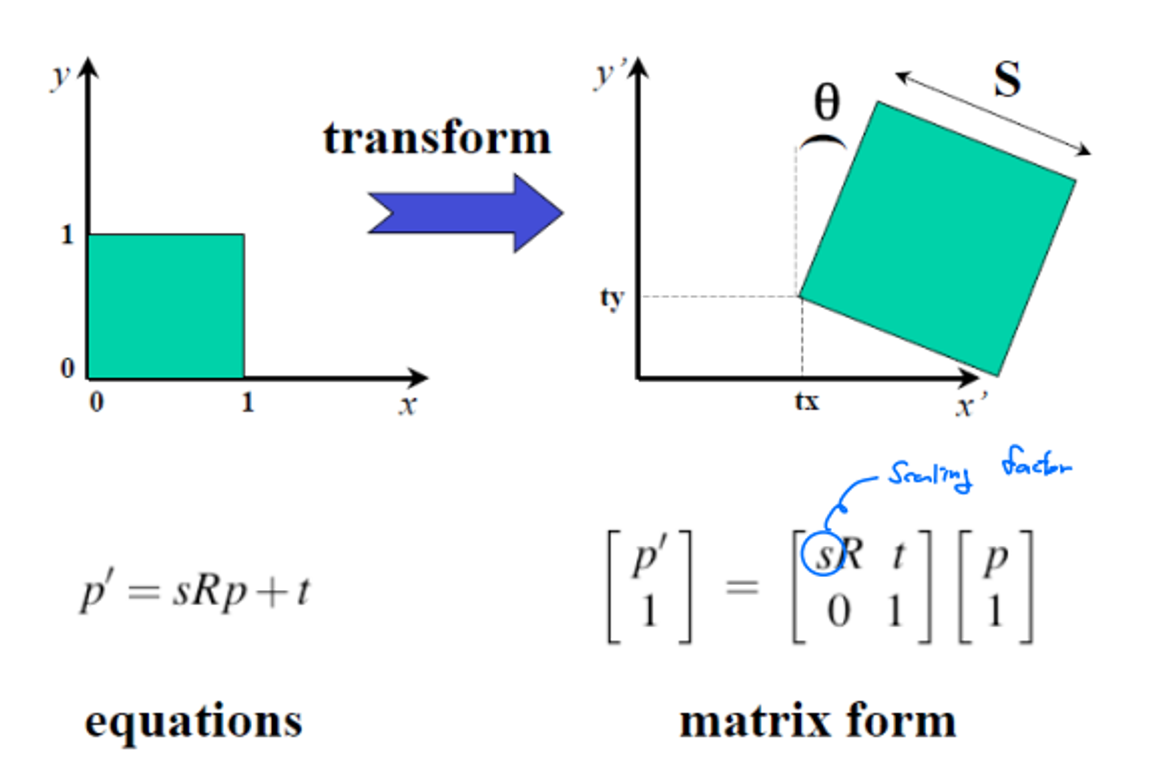
✅ Similarity
Scaled Euclidean = Scaling+ Translation + Rotation
2D
DoF=unknown parameter: 4
→
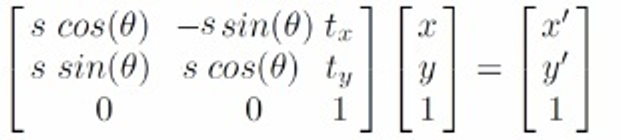
- 필요한 최소
corresponding point: 2
✅ Affine
not-uniform Scaling+ Translation + Rotation
2D
DoF=unknown parameter: 6
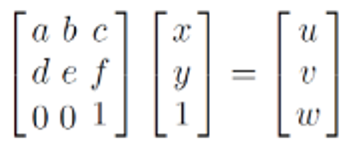
- 필요한 최소
corresponding point: 3
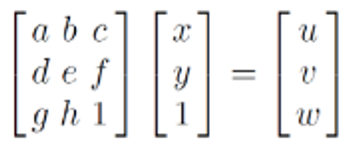
✅ Projective
2D
DoF=unknown parameter: 8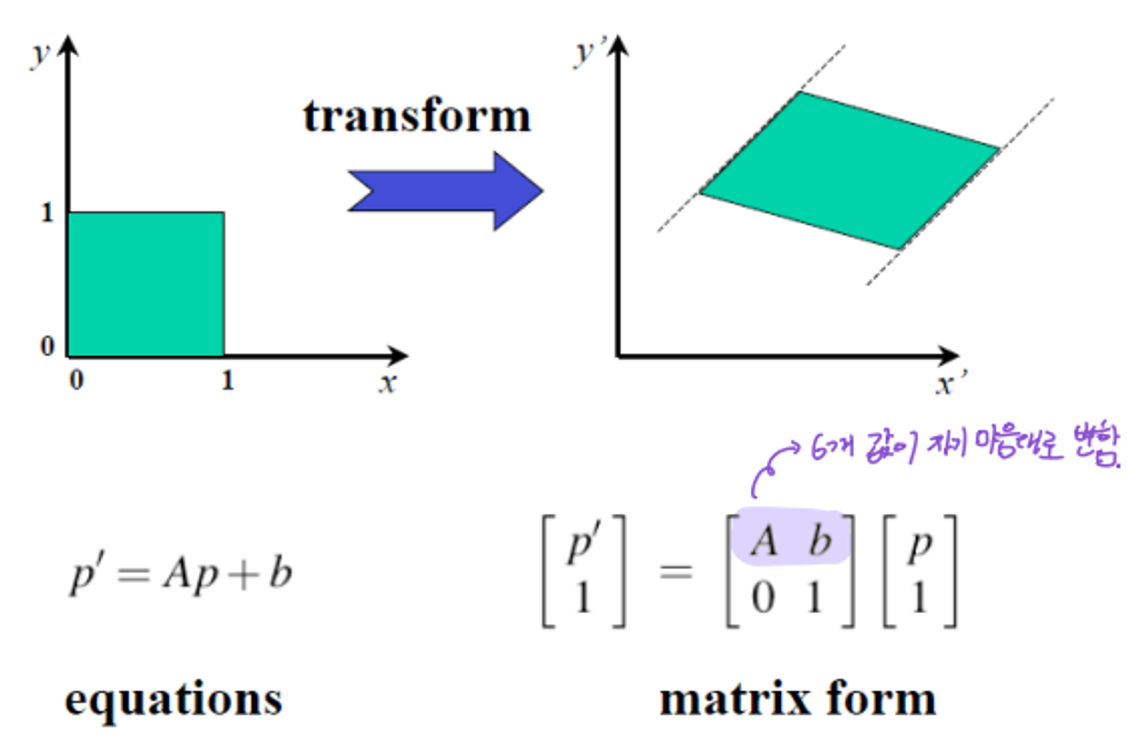
- 필요한 최소
corresponding point: 4