📌 MDP - Goals and Rewards

✔ Maximizing Rewards

The reward is a formalized signal about the agent’s goal.

• reward : 특정 state 마다 action을 했을 때 이에 대한 feedback으로 environment로부터 받는 것

• 각 timestamp에서 reward signal은 environment에서 agent로 전달이 된다.

• reward는 실수이다
  

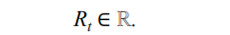
• 로봇 예시에서처럼 대부분의 시간에는 0의 리워드를 받고 캔을 주우면 1의 리워드를 받고 너무 많이 움지여서 배터리가 방전되면 -1의 리워드를 받는다

The agent always learns to maximize its reward.

• agent가 우릴를 위해 뭔가를 하기를 원한다면, reward를 그 행동을 잘 하게 만드는 방식으로 해야한다.
  → 강화학습에서 젤 어려운게 문제를 잘 정의하고 거기서 리워드를 잘 설정하는 것이 어렵다.
  
• reward라는 것이 진짜 우리가 달성하기를 원하는 것에 주어야 한다.
• agent한데 잘했다고 주는 way of communicating이라고 말할 수도 있다.

Maximizing Cumulative Reward over Episodes

Cumulative Reward

• 행동을 취했을 때 바로 reward가 들어오는 것이 아니다.
• 당장의 reward를 고려하는 것이 아니라 행동을 취하고 있다 보니까 한 20 초 뒤에 미래의 가장 reward가 높다. 이처럼 Cumulative Reward는 goal 을 롱 텀으로 바라보고 planning할 수 있도록 만들어 준다.

The return is the sum of the rewards.

• maximize the cumulative reward 장기 보상을 최적화
• expected return $G_t$ : sum of the rewards
  → 고려 가능한 곳까지 리워드를 더했을 때 얻을 수 있는 장기보상
  

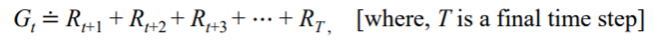
The episode is a sequence of actions, states, and rewards.

• episode : sequence of actions, states, and rewards, starting from an initial state and ending at a terminal state or a predefined time limit.

• The agent's learning process consists of multiple episodes

• What if T is infinite?
  a와 b 둘 다 시행해서 100의 리워드를 얻는데 a보다 b가 훨씬 더 오랜 시간이 걸린다면 어떻게 이를 구분할것인가?
  => 이를 해결하기 위해 discount factor(γ) 을 사용한다

Return Discounting

Adjusting the importance of future rewards relative to immediate rewards.

• γ : discount factor (between 0 and 1)
  → 최대한 빨리 목표를 달성해야 장기보상이 최대화된다.
  

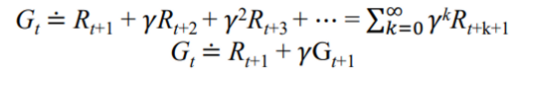
• A higher discount factor - future rewards
  → 장기보상에 초점
• a lower discount factor - immediate rewards
  → 현재 얻을 수 있는 단기 보상에 초점
  

• G is a sum of an infinite number of terms 이라 해도 일정 이상 곱해지면 0으로 가기 때문에 finite한 영역에서 정의 할 수 있다.

→ If the reward is constant +1

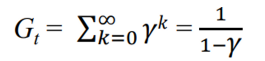
✔ Discounting if often used for a few reasons

• Modeling uncertainty
  장기적으로 큰 보상을 얻고자 할 때, 좀 더 미래를 보고 uncertain한 것을 가지고 오고 싶으면 높은 discount factor을 사용, 확실한 결론을 내리고 싶으면 작은 것을 사용
  
• Fast convergence
  → 조금더 빨리 수렴한다. 현재에 얻을 수 있는 보상에 집중하도록 만들어 조금 더 빨리 수렴
  
• Finite tasks
  → 무한히 고려해야하는 것들이 있을 때 문제를 풀 수 있도록 Finite하게 만들어줌

Adjusting the importance of future rewards relative to immediate rewards.

✔ If discounting is not used (γ = 1)
→ agent는 모든 future rewards를 동일한 importance로 가정하고 풀게 된다.

• Slow convergence

• Infinite returns

• Overemphasis on long-term consequences

=> 장기 보상을 너무 고려해서 현재 해야하거나 빨리 해야하는 행동들에 영향을 미친다.

✔ (γ = 0)
당장 눈 앞에 있는 것만 고려하는 근시안적인 것

✔ γ = 1 or T = ∞ (but not both)

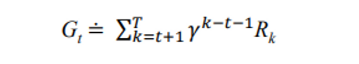
Return Example with Pole-Balancing

• Problem Definition

  • 카트가 쓰러지지 않도록 왼쪽 오른쪽 잘 조정하는 것
  • 카트가 트랙을 벗어나거나 폴이 떨어지면 실패

• Design as Episodic

  • 여러번의 에피소드를 거치면서 맞추려고 한다
  • 리워드는 tiime stamp에서 폴이 쓰러지지 않고 유지하면 +1 리워드
  • 폴을 영원히 떨어뜨리지 않으면 return이 무한대

• Design as Continuing Task

  • 폴을 유지하고 있는 동안에는 0 떨어뜨리면 -1 리워드
  • return $-γ^k$ 과 연관이 있으며, k는 실패할 때까지 걸린 시간.
    ⇒ 실패했을 때 패널티

---

📌 MDP – Policies and Value Functions

How good it is to perform a given action in a given state.
어떤 state에서 어떤 action을 취하는 것이 더 좋은걸까? 어떻게 판단할까?

✔ Policy

• π : policy, state에서 acion을 취할 확률
• 환경에서 agent가 어떻게 행동할지 결정하는 것
• 종류
  • Deterministic policy : 이 state에 오면 이 행동을 무조건 함
    → a = π(s)
  • Stochastic policy : s라는 state에서 a라는 action을 할 확률
    → P(a|s) = π(a|s) ⇒ 조건부가 오면 스토카스틱~

✔ Value functions

• expected cumulative rewards 를 평가하는 것.
• state에서 내가 할 수 있는 몇개의 action이 있는데
  → staion이 주어졌을 때 action들을 취했을 때 얻을 것으로 예상되는 expected cumulative rewards
  → 혹은 s, a1이 주어졌을 때 얻을 것으로 예상되는 expected return
  
• 행동의 가치를 평가함

State-value function (V-function) : $v_π(s)$

• state 자체의 value를 평가하는 것
• $v_π(s)$
  → value를 책정할건데 π 정책을 따를거고 이때 s라는 state에 있을때의 가치는?
  

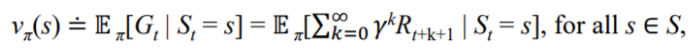
Action-value function (Q-function) : $q_π (s, a)$

• 어떤 state가 있을 때 교실에 있을 때 pc방에 가는 행동과 도서관에 가는 행동에 대한 가치
• s에서 시작해 action a를 취했을 때 policyπ 를 따라갔을 때 얻게 되는 리워드

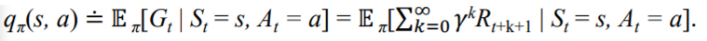
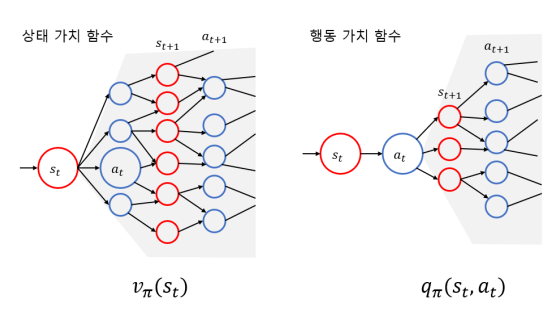
그림으로 상태 가치 함수와 행동 가치 함수를 보면 다음과 같다.

Value functions can be estimated from experience

Experience?

• 가치를 평가하기 위해서 실제로 그 state에 가서 action을 취해보고 어떤 reward를 얻었는지에 대한 정보가 필요하다
• 데이터를 모은다.
• 계속 어떤 업데이트를 하면서 더 좋은 방법을 찾아간다.

Monte Carlo (MC) methods
전이 확률을 모르는 경우 즉 MDP를 모를 때는 시용하는 방법이다.

• 반복된 시행을 통해 비율이나 평균으로 답을 유추해내는 맥락

• 여러번의 에피소드를 계속 돌리면서 거기서부터 평가한 것들을 평균시키는 것

• 에피소드가 처음 부터 끝가지 완료가 되어야 하고 task 자체가 에피소드 여러번을 거쳐서 되게 디자인되어야 한다.

• state-value function $v_π(s)$ 추정하기 위해
  → 모든 에피소드를하면서 s를 방문했던 에피소드들에 대해 관찰한 애들 데이터를 평균을 내보니 대충 이정도 나왔다고 판단
  

• action-value function $q_π (s, a)$
  → 에피소드들에서 얻었던 리워드들 평균내서 판단
  

• state와 action이 너무 크면 → MC는 효과적이지 않음
  에피소드를 많이 돌려도 해당 state가 몇 번 나오지 않아 평균을 내는 것도 의미가 없다.
  ⇒ 이걸 가능하게 하기 위해 parameterized function approximator 쓰는데 이건 수업에서 다루지 않음

Bellman Equation

Recursive relationships

• 현재에 뭐가 정해졌으면 이후 것을 정할 때
• policy π and any state s 가 있을 때
• $v_π(s)$ : state s가 주어졌을 때 return이 $G_t$가 나올 확률

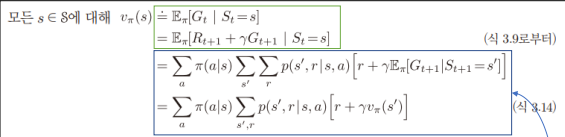
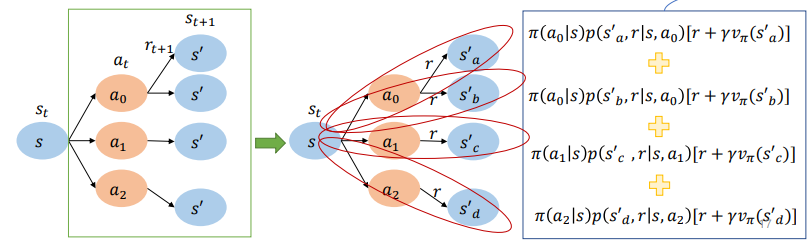
Backup diagram

• Open circle: state & solid circle: state-action pair.
• state s에서 어떤 것이든 action을 취할 수 있음
  → policy에 따라 확률이 나누어짐

---

📌Optimal Policies and Value Functions

Finding a policy that achieves a lot of reward over the long run

Optimal policy?

• 모든 state에서 π와 π’ 중에 더 좋은 것 π 를 택한다.
  

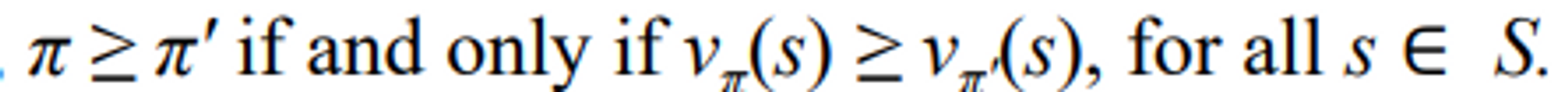
• There is always at least one policy that is better than or equal to all other policies: optimal policy
  -> denote all optomal policies by $π_*$

• They share the same state-value function, called the optimal state value function, denoted
  → max π : $v_π(s)$를 극대화시키는 π
  

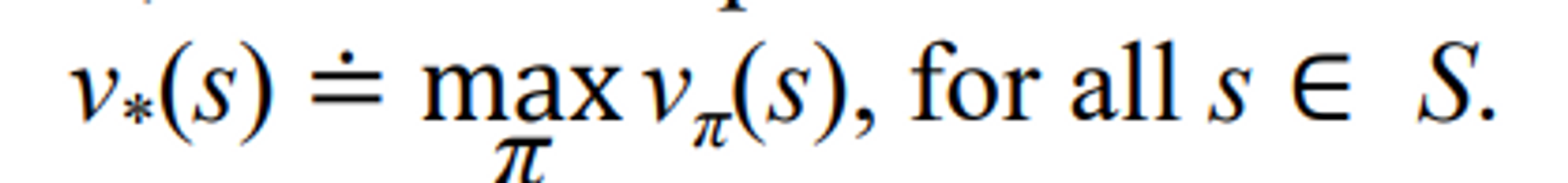
• Optimal polices also share the same optimal action-value function, denoted
  

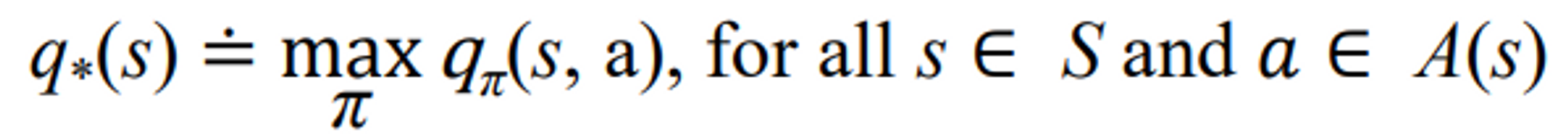
• For the state-action pair (s, a), this function gives the expected return for taking action a in state s and thereafter following an optimal policy
  

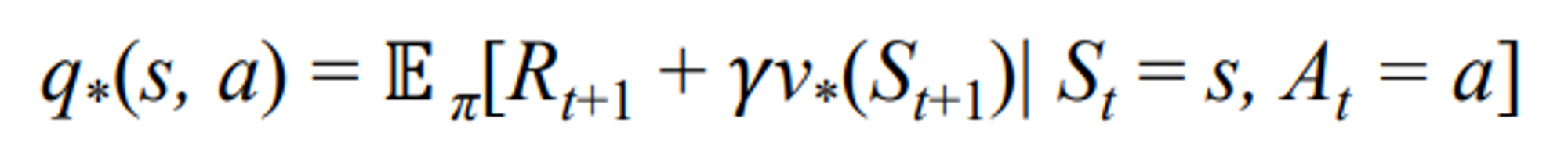
Finding Optimal policies and value functions is Indeed a challenging

최적 정책과 가치 함수를 찾는 것이 어려운 이유

• High computational complexity
  • environment’s dynamics가 정확하고 알고 있을 지라도 벨만 최적 방정식을 풀어 최적 정책을 계산하는 것은 보통 쉽지 않다.
  • 계산량은 항상 충분하지 않다.
• Memory shortage
  • 몬테카를로 같은거 하려면 다 저장해야 평균 낸다
  • 간단한 문제면 그냥 어레이나 테이블 같은 걸로 사용해 appproximation 하면 되는데 복잡해지면 불가
• Partial observability
  • 우리가 환경을 모두 fully observe하는 것이 어렵다.
  • partially observable Markov decision processes (POMDPs)
    → 환경의 모든 state를 다 알 수 없기 때문에 현재 내가 관찰한 것을 기준으로 결정을 내리겠다

---

🖇Reference

이 글은 강형엽 교수님의 게임공학[GE-23-1] 수업을 수강하고 정리한 내용입니다.
[mdpw] https://en.wikipedia.org/wiki/Markov_decision_process
[sutton] Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press
[value & action function] 황주영 조교님 강의자료