What Is Reinforcement Learning?
강화학습Reinforcement Learning이란 agent의 보상을 최대화할 수 있는 행동이 무엇인지를 학습하는 것이다.
- Agent : Environment에서 Action을 취할 수 있는 물체
- Environment : Agent와 상호작용을 하는 것으로, Agent에게 적절한 state를 부여함
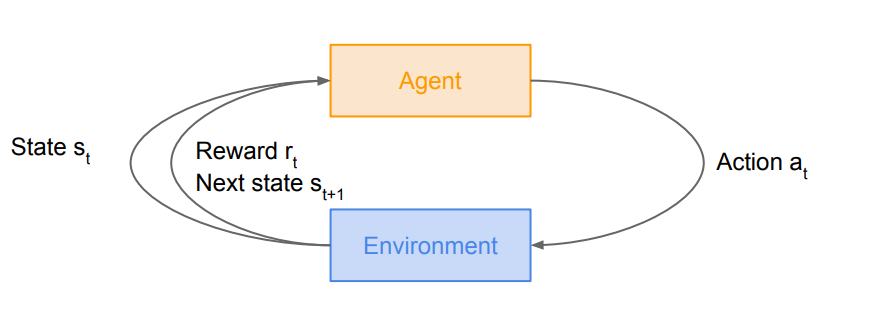
작동 과정을 보면 환경에서 agent에게 상태가 주어진다. 그러면 agent는 어떤 action을 취하게 되고, 그러면 환경은 action에 따라 agent에게 보상을 주고 다음 state를 부여한다.
또 이러한 과정은 agent가 종료 상태(terminal state)가 될 때까지 반복한다.
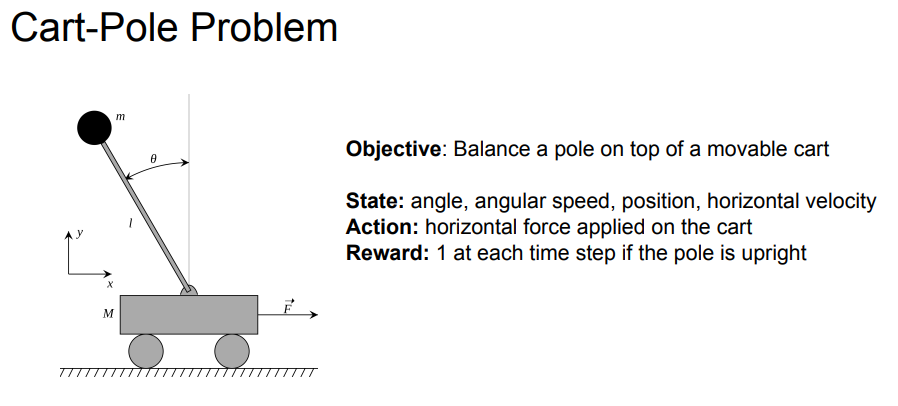

강화 학습으로 사진과 같은 문제들을 풀 수 있다.
Markov Decision Processes
Markov Decision Processes는 강화 학습을 수식으로 나타내는 것이다. 즉 강화학습 문제를 수식화 시킬 수 있다.
MDP는 Markov property를 만족한다. Markov property란 현재 상태만으로 전체 상태를 나타내는 성질이다. 다음과 같은 기호들로 정의된다.

- S: 가능한 상태
state들의 집합 - A: 가능한 행동
action들의 집합 - R: (state, action) 쌍이 보상으로 매핑되는 함수(보상의 분포)
- P: 전이 확률, (state, action) 쌍이 주어졌을 때 전이될 다음 state에 대한 분포
- γ: discount factor(보상을 받는 시간에 대해 얼마나 중요하게 생각할 것인지)

결국 수식을 풀어 쓰면 최적의 policy π*를 찾는 것을 목표로 하게 된다. 즉 cumulative discounted reward를 최대화시키는 것이다.

최적의 policy인 π*는 reward의 합을 최대화시키므로 reward의 합에 대한 기댓값을 최대화시키면 된다.
이제 최적의 정책을 찾는 방법을 다루기 전에, 몇 가지 정의를 먼저 살펴보려 한다.
- Value function: state s와 policy π가 주어졌을 때 누적 보상의 기댓값
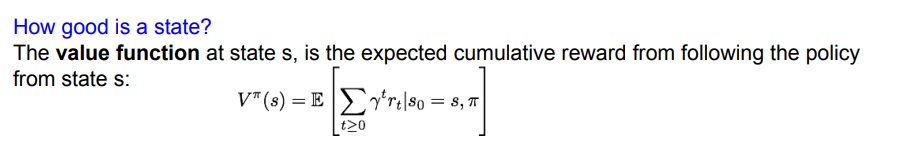
- Q-Value function: policy π, action a, state s가 주어졌을 때 받을 수 있는 누적 보상의 기댓값
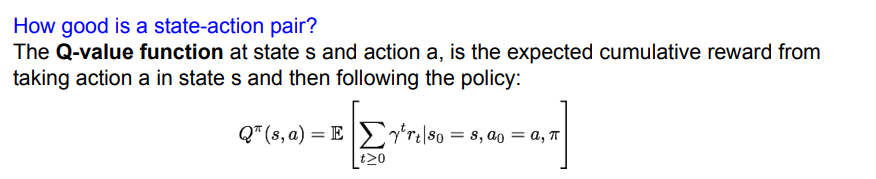
Bellman equation
Bellman equation은 강화학습에서 중요한 요소 중 하나이다.

최적의 policy로부터 나온 Q-value function인 Q*가 있다고 가정하면, Q*는 bellman equation을 만족할 것이다. 즉 우리가 이미 최적의 policy를 알고 있기 때문에 s'에서도 최적의 action을 취할 수 있다.
따라서 그저 policy를 따라 action을 취하기만 하면 최상의 reward를 받을 수 있다는 것이다.
그렇다면 어떻게 최적의 policy를 구할 수 있을까? 바로 value iteration algorithm을 이용하는 것이다.
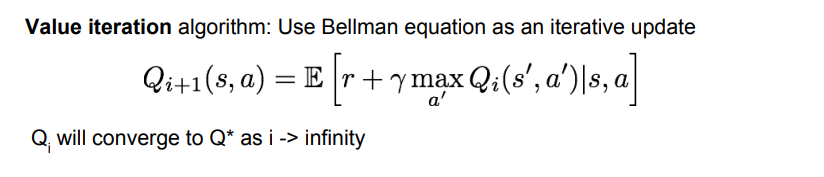
반복적인 업데이트를 할 때 bellman equation을 이용하고, 각 step마다 Q*를 조금씩 최적화시킨다. 수학적으로 보면 i가 무한대일 때 최적의 Q*로 수렴하게 된다. 하지만 문제가 있는데, 바로 이 방법은 scalable하지 않다는 점이다.
반복적으로 업데이트하기 위해서는 모든 (s,a)마다 Q(s)를 계산해야 하는데 전체 상태 공간이 아주 크면 불가능하다.
따라서 해결책으로 Q(s,a)를 근사할 수 있는데 이때 Neural Network를 사용한다.
Q-Learning
Neural Network를 사용해서 Q(s,a)를 근사시키는 것을 deep Q-learning이라고 한다. 요즘의 강화학습에서 빠지지 않고 등장하는 방법이라고 한다.

Forward Pass에서는 손실 함수를 계산한다. 손실이 작을수록 좋다.
Backward Pass에서는 계산한 손실을 기반으로 파라미터 𝜃를 업데이트한다.

이렇게 반복적인 업데이트를 통해 우리가 가진 Q-function이 타겟값과 가까워지도록 학습한다.
예시로 atari game을 들어 설명해 보면
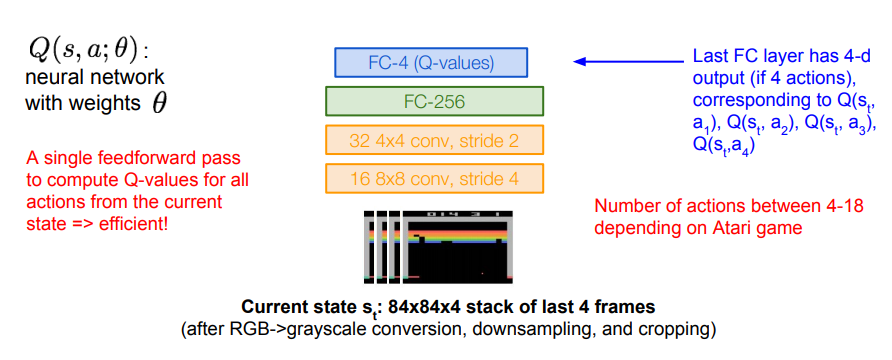
네트워크의 입력은 state s이다. 즉 현재 게임 스크린의 픽셀들이 입력으로 들어온다.
전처리 과정을 거친 후, input은 84 x 84 x 4의 형태가 된다.
FC layer의 출력 벡터는 네트워크의 입력인 state가 주어졌을 때 각 행동의 Q-value값이다. 상,하,좌,우 4가지가 존재하므로 총 4개의 벡터로 출력된다.
이러한 방식의 네트워크 구조의 장점은 모든 Q-value를 한 번의 forward pass로 계산할 수 있다는 점이다.
Experience Replay
Q-network를 학습할 때 알아야 하는 개념 중 하나가 experience replay이다. 이는 Q-network에서 발생할 수 있는 문제들을 다룬다.
Q-network를 학습시킬 때 하나의 배치에서 연속적인 샘플들로 학습하면 결과가 좋지 않다. 모든 샘플이 상관 관계(correlation)을 가지기 때문이다.
또 네트워크가 우리가 어떤 action을 취할지 policy를 결정할 때 다음 샘플들도 결정해버리는 문제가 생긴다.(bad feedback loops)
따라서 이를 해결하기 위한 방법이 experience replay이다. 이 방법은 replay memory를 이용하는데, 더 많은 경험을 얻어 전이 테이블을 지속적으로 업데이트한다. 따라서 연속적인 샘플을 이용하는 대신 전이 테이블에서 임의로 샘플링된 샘플을 사용한다.
이 방법을 사용하는 또 하나의 이유는 각각의 전이가 가중치 업데이트 과정에 여러 번 기여할 수 있게 되어 데이터 효율이 훨씬 증가하기 때문이다.

사진은 experience replay의 pseudo 코드이다.
Policy Gradients
지금까지 살펴본 Q-Learning에도 문제점이 존재한다. 바로 Q-function이 너무 복잡하다는 것이다. Q-Learning에서는 모든 (s,a) 쌍들을 학습해야만 한다. 하지만 모든 경우의 수를 학습시키는 것은 너무 어려운 문제이다.
다른 한편으로는 policy 자체를 학습시키는 것은 간단하다.
그 방법을 Policy Gradients라고 한다.

J(𝜃)는 미래에 받을 보상들의 누적 합의 기댓값으로 나타낼 수 있다. 지금까지 사용했던 reward와 동일하다.
여기서 우리가 하고 싶은 것은 최적의 정책인 𝜃*를 찾는 것이다.

여기에서는 policy parameter에 대해서 gradient ascent를 수행하는 방식으로 진행하였다.
REINFORCE algorithm에 대해 좀 더 구체적으로 살펴보면, gradient ascent 방법을 사용하기 위해 식을 미분해야 하는데 미분값을 계산할 수 없다. (intractable)
따라서 이를 해결하기 위한 트릭으로 식을 조금 바꿔 준다.

그러면 계산이 가능한 식으로 바뀌게 된다.

우리는 p(𝜏 ; 𝜃) 를 전이확률을 모르는 채로 계산할 수 있을까? 우리가 log 함수를 이용하게 되면 곱이 모두 합의 형태로 바뀌게 되는데, 따라서 관련 있는 항만 계산하면 되므로 구체적인 Q-value를 몰라도 policy 자체의 gradient를 구해 최적의 policy를 찾을 수 있다.
Variance reduction
우리가 어떤 policy를 찾았을 때 그 policy에 포함된 action를 좋았다고 평가하는데 Average out 때문에 구체적으로 어떤 action이 good policy를 만드는지는 알지 못한다. 따라서 분산을 줄이는 것이 policy gradient에서 아주 중요한 분야이다. 이는 샘플링을 더 적게 하면서도 estimator의 성능을 높일 수 있는 방법이기도 하다.

해결할 수 있는 아이디어가 크게 두 가지 소개되었는데
- First idea : 해당 state로부터 받을 미래의 reward만을 고려하여 어떤 action을 취할 확률을 키워주는 방법
이 방법의 의도는 어떤 action이 발생시키는 미래의 reward가 얼마나 큰 지를 고려하겠다는 것이다.
- Second idea : 지연된 reward에 대해서 discount factor를 적용하는 방법
discount factor가 의미하는 것은 지금 당장 받을 수 있는 보상과 조금 늦게 받은 보상간의 차이를 구별하는 것이다. 즉 어떤 action이 좋은 action인지 아닌지를 가까운 곳에서 찾는다.
- Third idea :
baseline
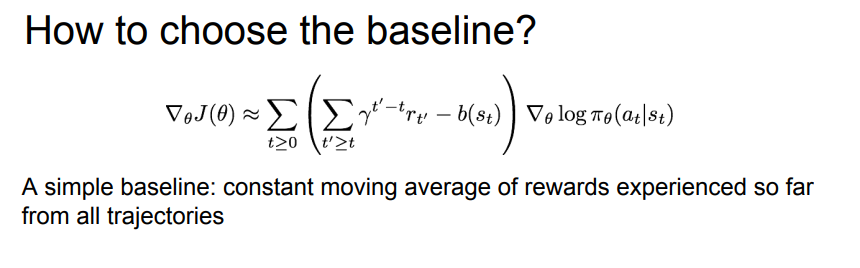
경로에서 계산한 값을 그대로 사용하지 않고 baseline function을 이용한다. baseline 함수는 해당 상태에서 우리가 얼마만큼의 reward을 원하는지를 나타낸다. 이를 통해 우리가 기대했던 것에 비해 reward가 좋은지 아닌지에 대한 상대적인 값을 얻을 수 있다.
baseline을 선택하는 방법은 가장 단순하게는 지금까지의 reward의 moving average를 취하는 것이다.
그렇다면 더 좋은 baseline은 무엇일까?
바로 Q-function과 value function을 이용할 수 있다. 하지만 구체적인 function이 무엇인지 알 필요는 없다.
바로 Policy gradient와 Q-Learning을 이용하여 training시킬 수 있다.
이를 Actor-Critic Algorithm이라고 한다.

- Actor : Policy, 어떤 action을 취할지 결정
- Critic : Q-function, 그 행동이 얼마나 좋았고 어떤 식으로 조절해 나가야 하는지 알려줌
