1. Leetcode #1342 문제
양의 정수 num이 주어졌을 때 num을 0까지 줄여가는 과정을 작성하는 문제인데 현재 숫자가 짝수인 경우 2로 나누고 홀수인 경우는 1을 빼야한다.
몇 번이나 과정을 반복했는지를 리턴해야 한다.
입출력 예시
Input: num = 14
Output: 6
Explanation:
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.제한사항
0 <= num <= 10^6
나의 풀이
var numberOfSteps = function(num) {
let count = 0;
while (num) {
if (num % 2 === 0) {
num = num / 2;
count++;
}
if (num % 2 !== 0) {
num = num - 1;
count++;
}
}
return count;
};횟수를 리턴해야하니 count라는 변수를 선언 후 num 만큼 while 반복문을 돌리고 짝수, 홀수의 경우를 판단하여 나온 결과를 num에 저장하고 count를 증가시켜주었다. 나의 경우 런타임은 48ms 메모리 사용은 33.7MB가 나왔다.
다른사람의 풀이
var numberOfSteps = function(num) {
let numSteps = 0;
while (num != 0) {
if (num%2 == 0) {
num /= 2;
} else {
num -= 1;
}
numSteps++;
}
return numSteps;
};Leetcode에 있는 것 중 가장 빠른 런타임을 가진 코드이다. 런타임이 28ms밖에 안된다. 로직은 똑같은데 연산 과정의 차이인가.. 시간복잡도를 구해보고 싶은데 아직은 잘 모르겠다.
2. Leetcode #1108 문제
IPv4 형식의 임의의 IP 주소가 주어지면 . 으로 구분되어 있는 주소를 [.]으로 교체하는 문제이다.
입출력 예시
Input: address = "255.100.50.0"
Output: "255[.]100[.]50[.]0"제한사항
- The given address is a valid IPv4 address.
나의 풀이
var defangIPaddr = function(address) {
return address.split('.').join('[.]');
};
split 메소드를 이용하여
.을 기준으로 나눈 후 join 메소드로 다시[.]로 구분하였다. 정규표현식을 이용하고 싶었으나 아직 공부하지 않아서 패스. 메소드는 내장함수이기 때문에 상대적으로 연산이 오래걸리는 것 같다. 코드는 깔끔해 보이나 성능면에선 👎 런타임은 40ms가 나왔다.
다른사람의 풀이
var defangIPaddr = function(address) {
return address.replace(/\./g, '[.]');
};정규표현식을 이용하여 전역에서
.탐색해[.]로 교체해주었다. 런타임은 28ms 유의미한 성능 차이는 아닌 것 같지만.. 그래도 정규표현식으로 작성한 코드는 뭔가 멋있어 보인다..
3. 시간복잡도와 Big-O 표기

요즘 알고리즘 문제들을 하루에 몇 문제 정도 풀고 있는데 런타임이 오래걸리는 코드들을 어떻게 개선할 수 있을까에 대해 찾아보다가 시간복잡도와 Big-O라는것을 발견하게되었다.
예를 들어, 케이크 하나를 자르는데 여러가지 방법으로 자를 수 있는 것처럼 한 문제를 여러가지의 알고리즘으로 풀 수 있다. 시간복잡도를 분석하는 것은 input n에 대하여 알고리즘이 문제를 해결하는 데에 얼마나 오랜 시간이 걸리는 지를 분석하는 것과 같다. 그리고 이를 Big-O 표기를 이용하여 정의할 수 있다.
시간복잡도에서 중요한 것은 정해진 표현식에 가장 큰 영향을 미치는 n의 단위이다.
시간복잡도의 정의
- O(1) - 상수 시간: 입력 데이터의 크기와 상관없이 언제나 일정한 시간이 걸리는 알고리즘
- 입력되는 데이터양과 상관없이 일정한 실행 시간을 가짐.
- 알고리즘이 문제를 해결하는데 오직 한 단계만 거침.
- O(log n) - 로그 시간: 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
- 데이터양이 많아져도, 시간이 조금씩 늘어남.
- 시간에 비례하여 탐색 가능한 데이터양이 2의 n승이 됨.
- 주로 커다란 문제를 일정한 크기를 가지는 작은 문제로 쪼갤때 나타나는 유형
- O(n) - 직선적 시간: 입력 데이터의 크기에 비례
- 데이터양에 따라 시간이 정비례함.
- 대표적으로 for 문이 있음.
- O(n^2) - 2차 시간: 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱.
- 데이터양에 따라 걸리는 시간은 제곱에 비례(효율성 👎)
- 이중 반복문에서 처리 하는 경우에 나타나는데, n값이 커지면 실행 시간은 감당하지 못할 정도로 커지게 됨.
- O(C^n) - 지수 시간: 문제를 해결하기 위한 단계의 수는 주어진 상수값 C의 n 제곱.
- 🤮
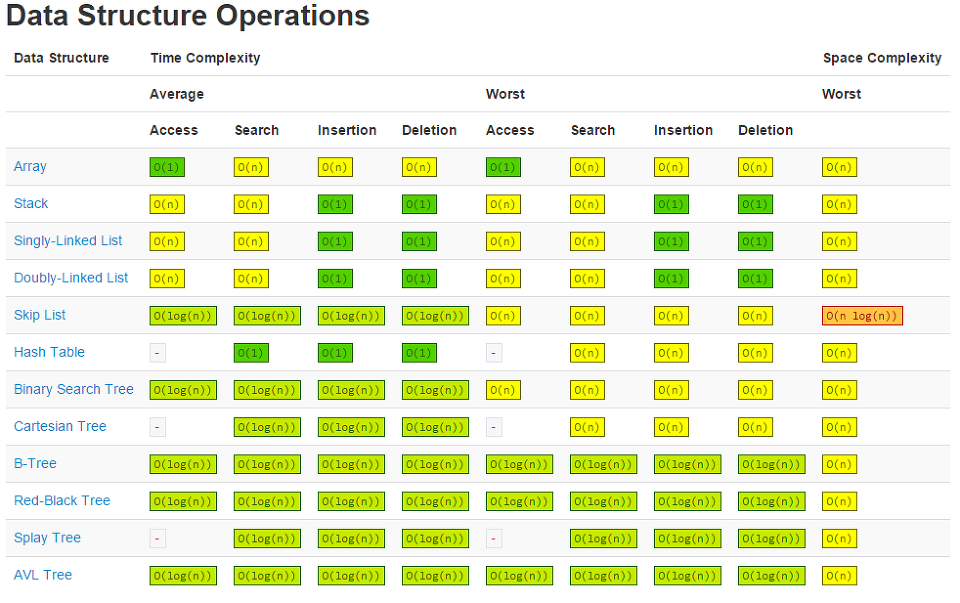
각 자료구조별 시간복잡도 분석