SDEdit

gpt4.5로 작성됨.

1. 들어가며

기존의 GAN(Generative Adversarial Network) 기반 방법들은 사용자의 입력과 사실적 이미지 간 균형을 유지하는 데 어려움이 있었고, 매번 새로운 데이터 수집 및 학습 과정이 필요했다. 이에 대한 대안으로 등장한 것이 바로 SDEdit(Stochastic Differential Editing)이다.

2. SDEdit란?

SDEdit는 확률적 미분 방정식(SDE, Stochastic Differential Equation)을 활용한 이미지 생성 및 편집 방법으로, 확산(diffusion) 모델의 원리를 기반으로 한다. 사용자의 입력(예: 간단한 색상 스트로크, 이미지 패치 등)을 받아 이 입력에 가우시안 잡음을 추가한 후, 이를 다시 제거하는 과정을 반복하여 현실적이고 사용자의 의도에 충실한 이미지를 생성한다.

기존 방식과의 차별점:

• 조건부 GAN(Conditional GAN): 매번 새로운 작업에 맞춰 데이터 수집과 재학습이 필요했다.
• GAN Inversion: 복잡한 역추적 과정과 작업별 손실 함수 설계가 필요하며, 때로는 입력을 충실히 표현하지 못하는 문제점이 있었다.

SDEdit는 이 두 방식의 문제를 해결하며, 별도의 재학습 없이 범용적인 이미지 편집 및 생성을 지원한다.

3. SDEdit의 핵심 개념

SDE(Stochastic Differential Equation)의 이해

• SDE는 일반적인 미분 방정식에 무작위 노이즈를 더한 것이다. 이미지 생성에서 이 SDE는 원본 이미지를 잡음으로 서서히 변환한 뒤, 이 과정을 역으로 수행하여 잡음에서 사실적인 이미지를 얻는 방식이다.

VE-SDE(Variance Exploding SDE)와 VP-SDE(Variance Preserving SDE)

• VE-SDE: 시간이 지남에 따라 노이즈가 점점 커져 마지막에는 이미지가 순수한 잡음에 가까워진다.
• VP-SDE: 데이터의 분산을 유지하면서 점점 잡음으로 변환한다.

SDEdit는 특히 VE-SDE를 기반으로 설명된다.

4. SDEdit의 알고리즘

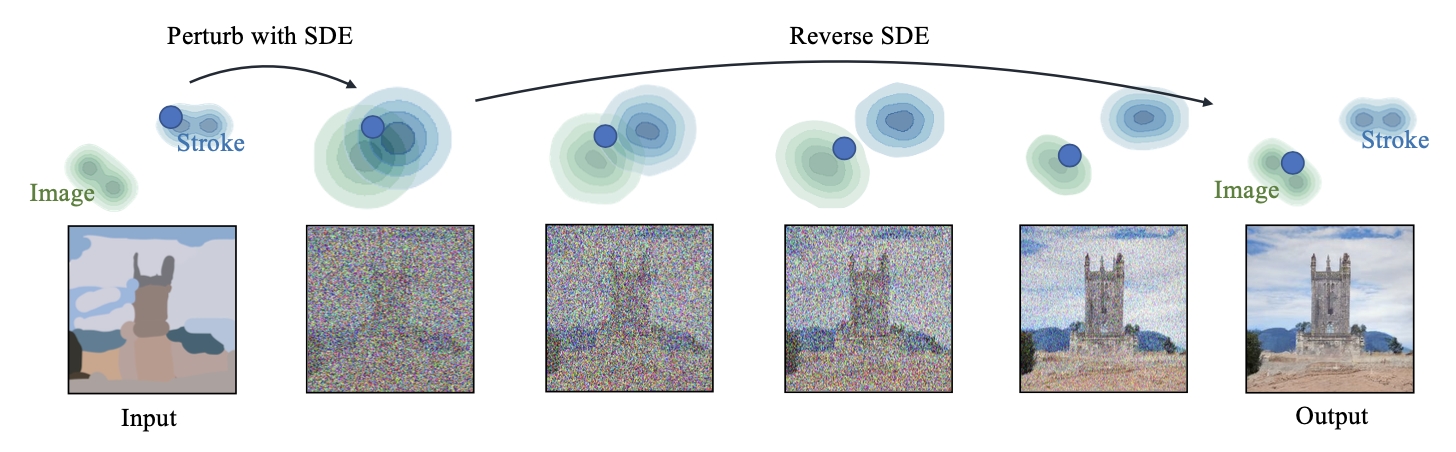
사용자로부터 가이드 이미지(간단한 스트로크 등)를 입력받아 다음의 과정을 수행한다:

1. 가이드 이미지에 적절한 수준의 가우시안 노이즈를 추가한다.
2. 이 노이즈가 추가된 이미지로부터 역방향 SDE를 반복적으로 적용하여 노이즈를 점점 제거한다.
3. 최종적으로 사실적이며 입력에 충실한 이미지를 얻는다.

이 과정에서 중요한 하이퍼파라미터는 t₀(노이즈 추가 정도)이며, 이 값이 클수록 사실성은 증가하지만 입력 충실도는 감소하는 trade-off가 있다.

5. 수식으로 이해하는 SDEdit

SDEdit의 핵심은 확률적 미분 방정식(SDE)을 활용해 이미지를 점점 사실적인 방향으로 복원하는 것이다. 이 과정은 수식적으로 다음과 같이 표현된다:

1) Forward SDE (노이즈 추가 과정)

SDE 모델은 원본 이미지 $\mathbf{x}(0)$에 시간에 따라 점점 강해지는 가우시안 노이즈를 더해 $\mathbf{x}(t)$를 만든다:

$\mathbf{x}(t) = \alpha(t)\mathbf{x}(0) + \sigma(t)\mathbf{z}, \quad \mathbf{z} \sim \mathcal{N}(0, \mathbf{I})$

• $\alpha(t)$: 원본 이미지 정보의 가중치
• $\sigma(t)$: 노이즈의 세기를 조절하는 함수

2) Reverse SDE (노이즈 제거 과정)

이제 $\mathbf{x}(t)$에서 다시 원본 이미지로 되돌아가는 과정은 다음과 같은 역방향 확률 미분 방정식으로 표현된다:

$d\mathbf{x}(t) = \left[ -\frac{d[\sigma^2(t)]}{dt} \nabla_{\mathbf{x}} \log p_t(\mathbf{x}) \right] dt + \sqrt{\frac{d[\sigma^2(t)]}{dt}} d\bar{w}$

기호	의미	해석
$\mathbf{x}(t)$	시간 $t$일 때의 노이즈 이미지	시작은 노이즈 이미지
$\frac{d\sigma^2(t)}{dt}$	노이즈의 변화율	시간이 줄어들수록 노이즈를 얼마나 제거할지 결정
$\nabla_{\mathbf{x}} \log p_t(\mathbf{x})$	노이즈가 낀 데이터의 분포에 대한 score function	현재 이미지가 진짜일 확률의 기울기 방향
$d\bar{w}$	역방향 시간의 Wiener process (확률적 변화량)	Brownian motion (무작위성 보존)

• $\frac{d\sigma^2(t)}{dt}$:

  • $\sigma^2(t)$:시간 t에 따른 노이즈의 분산 (시간이 지나면서 이미지에 점점 더 많은 노이즈를 섞어야 하기 때문)
  • 시간 t가 0에서 1로 갈수록 노이즈의 강도가 점점 커져야 함.

  $d\mathbf{x}(t) = -\underbrace{\frac{d\sigma^2(t)}{dt}}_{\text{줄어드는 속도}} \cdot \underbrace{\nabla_x \log p_t(x)}_{\text{복원 방향}} \cdot dt + \underbrace{ \sqrt{ \frac{d\sigma^2(t)}{dt} } }_{\text{무작위성 크기}} \cdot d\bar{w}$

확률 미분이란?

딥러닝에선 현실세계의 랜덤성을 부여하기 위해 확률 미분을 사용한다.
$dx(t) = a(t, x)dt + b(t, x)dW_t$

• $dx(t)$: 시간 $t$에서의 아주 작은 변화량. 여기에 무작위성이 포함.
• $a(t, x)dt$: 일반적인 변화 (기울기)
• $b(t, x)dW_t$: 랜덤성 추가

3) 학습: Score Matching Loss

모델은 score function을 다음과 같은 손실 함수를 통해 학습한다:

$L_t = \mathbb{E}_{\mathbf{x}(0) \sim p_{\text{data}}, \ \mathbf{z} \sim \mathcal{N}(0, \mathbf{I})} \left[ \left\| \sigma_t s_\theta(\mathbf{x}(t), t) - \mathbf{z} \right\|^2 \right]$

기호	의미
$\mathbf{x}(0)$	실제 데이터 이미지 (예: 학습 이미지)
$\mathbf{z} \sim \mathcal{N}(0, \mathbf{I})$	표준 정규분포에서 샘플링한 노이즈
$\mathbf{x}(t) = \alpha(t)\mathbf{x}(0) + \sigma(t)\mathbf{z}$	Forward SDE로 노이즈를 섞은 중간 상태 이미지
$s_\theta(\mathbf{x}(t), t)$	네트워크가 학습하려는 score function, 즉 노이즈의 방향을 추정함
$\sigma_t$	시간 $t$에서의 노이즈 세기
$\mathbb{E}[\cdot]$	전체 데이터와 노이즈에 대해 평균을 구함

지금 이 이미지에는 어떤 노이즈가 섞여 있는지 맞춰봐! 이 이미지가 진짜 이미지라면, 어떤 방향으로 noise를 제거하면 될까?를 학습 한다.

4) 샘플링: Euler-Maruyama로 구현

실제 샘플링은 역방향 SDE를 유한 시간 간격으로 근사하여 아래와 같이 구현된다:

$\mathbf{x}(t) = \mathbf{x}(t + \Delta t) + (\sigma^2(t) - \sigma^2(t + \Delta t)) s_\theta(\mathbf{x}(t), t) + \sqrt{\sigma^2(t) - \sigma^2(t + \Delta t)} \mathbf{z}$

이를 반복함으로써 점차 현실적인 이미지를 얻는다.

6. 실험 및 결과

SDEdit는 다음과 같은 다양한 이미지 작업에서 탁월한 성능을 보였다:

• 스트로크 기반 이미지 생성
• 이미지 합성(Image compositing)
• 스트로크 기반 이미지 편집

특히, 인간의 평가에서 기존 GAN 기반 방법들보다 현실성에서는 최대 98.09%, 전체 만족도(현실성+입력 충실도)에서는 최대 91.72% 더 높은 평가를 받았다.

7. SDEdit의 장점 요약

• 범용성: 별도의 데이터 수집이나 모델 재학습 없이 다양한 이미지 작업을 지원한다.
• 사실성과 충실도의 균형: 사용자의 의도를 정확히 반영하면서도 매우 현실적인 이미지를 생성할 수 있다.
• 간단한 적용: 기존에 미리 학습된 SDE 기반 모델을 바로 활용할 수 있다.

8. 의의

• 확산 모델의 표현력 활용: SDEdit는 확산 모델이 가진 고해상도 이미지 생성 능력을 편집 작업에도 효과적으로 활용.
• GAN의 한계 극복: 기존 GAN 기반 방식이 가진 재학습, 최적화 불안정성, latent space 제약 등의 한계를 해결..
• 재학습 없이 다양한 편집 가능: 한 번 학습된 확산 모델만으로 스트로크 기반 생성, 편집, 이미지 합성까지 수행할 수 있어 실용성이 높다.
• 조건부 생성의 새로운 방향 제시: 확산 모델에서 사용자 가이드를 중간 노이즈 수준(t₀)에서 삽입하는 방식은 이후 다양한 diffusion 기반 편집 모델에 영향을 주었다.

참고

• Chenlin Meng et al., "SDEdit: Guided Image Synthesis and Editing with Stochastic Differential Equations", Stanford University, 2022.