서론

용액 붓는 모바일 게임을 하다가, 문득 이걸 이용해서 알고리즘 문제를 만들 수 있을 것 같아서 한번 제작해 보았다. 무조건 백준 같은 문제에 이미 있을 것 같긴 한데, 한번 풀어보자. 참고로, 나도 아직 풀지는 않았다.

문제 - 용액 붓기

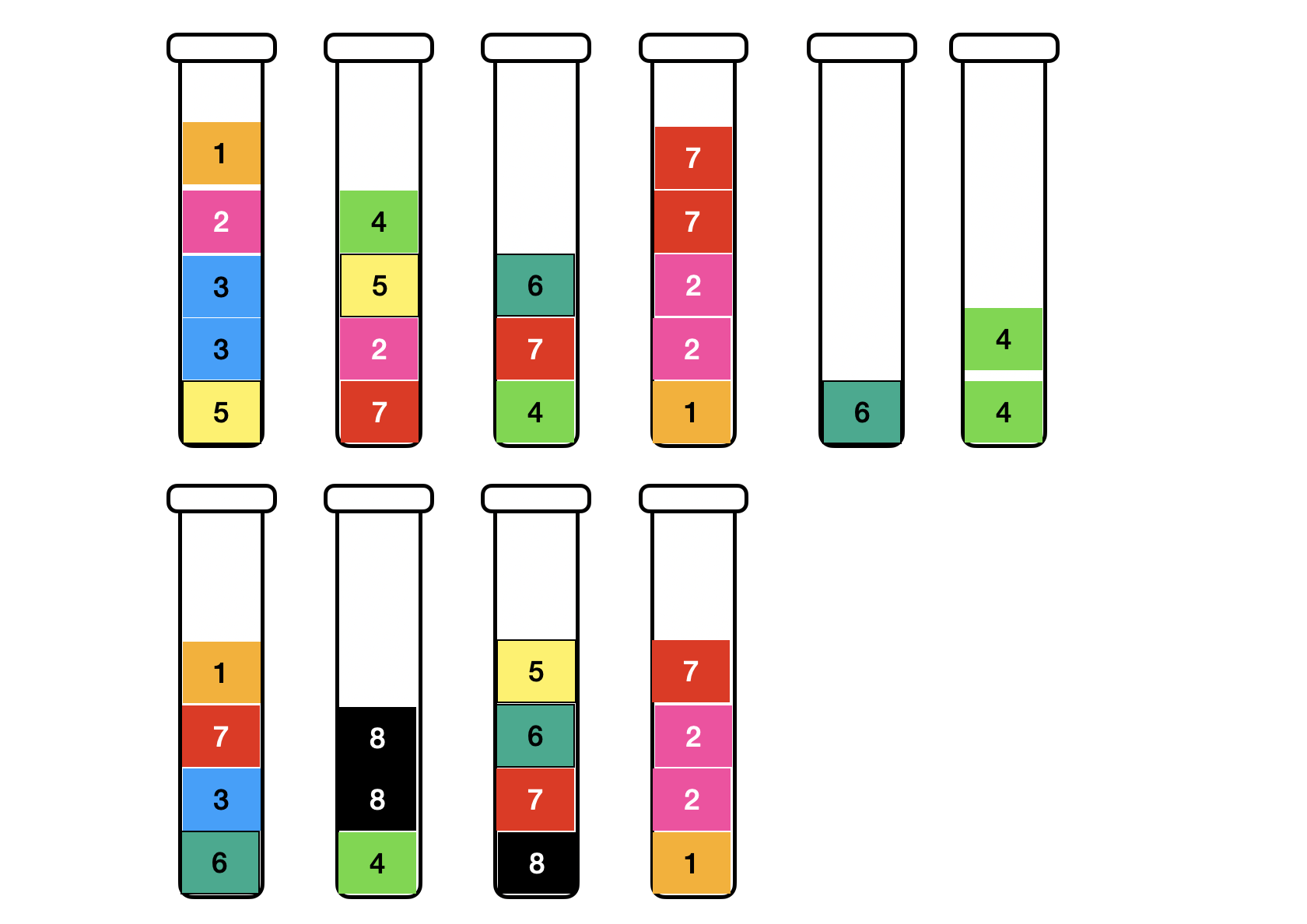
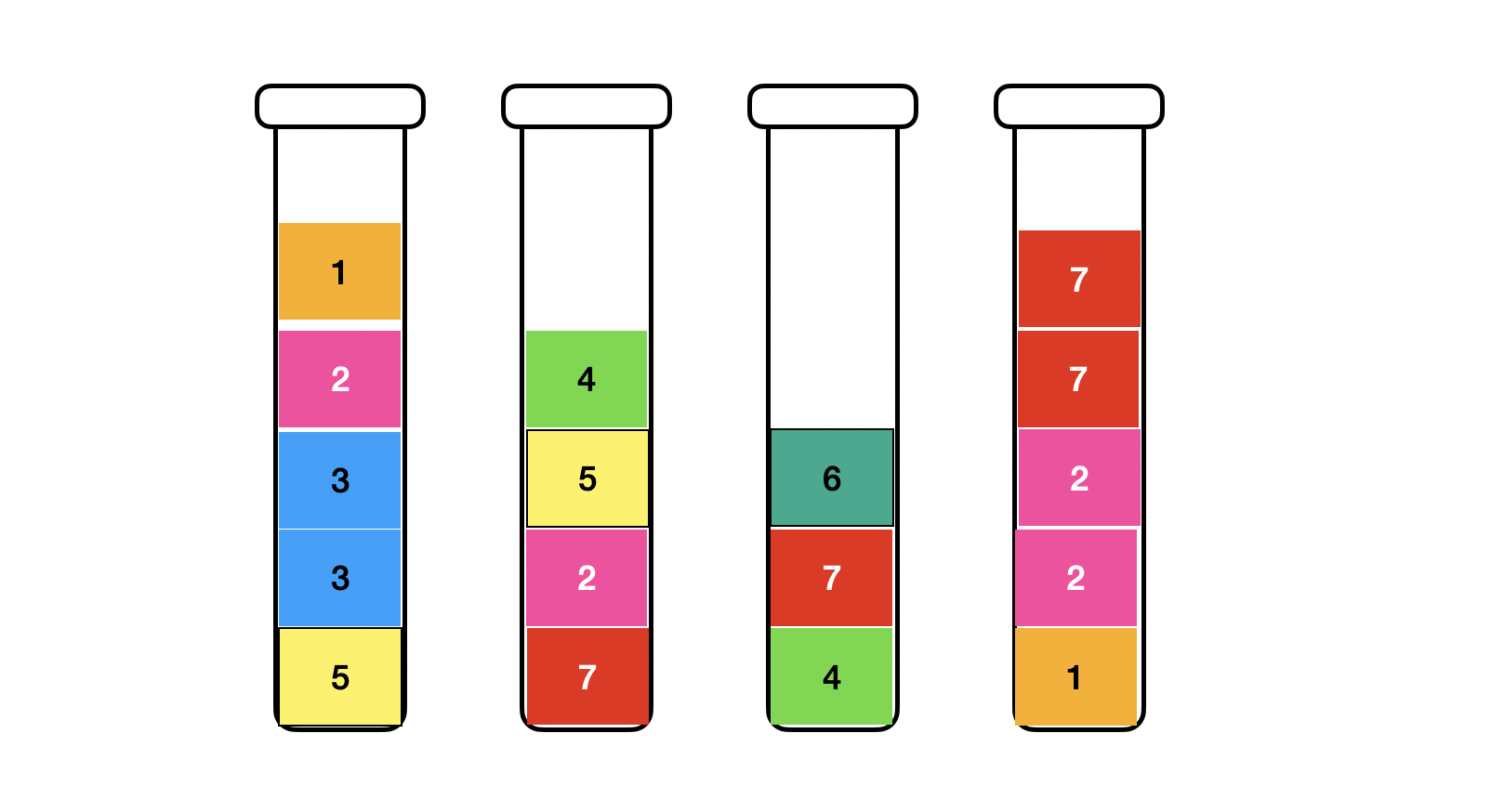
철수는 10가지의 시험관을 가지고 있고, 시험관에는 총 여덟 가지의 용액이 층을 이루어 담겨져 있다. 용액들은 서로 섞이지 않으며 반드시 층을 이루고 있다.

[0,1,2,3,3,5]은 시험 관의 맨 위는 비어져 있고, 순서대로 1번 용액, 2번 용액, 3번 용액이 두 층, 5번 용액이 쌓여 있는 것을 의미한다. 그림의 첫 번째 시험관과 같은 모양이다. 즉, 배열의 맨 앞이 시험관의 맨 위, 그리고 배열의 맨 뒤가 시험관의 맨 밑을 의미하는 것이다. 또한, 0은 용액이 그 층에 없다는 뜻이다.

규칙:

1. 용액과 용액 사이에는 빈 공간이 없다. 즉, [0,0,3,0,2,2]는 불가능한 상태이다. 3번 용액과 2번 용액 사이에 빈 공간이 있기 때문이다. 단, [0,0,3,1,2,2]는 가능하다.

2. 한 시험관에서 다른 시험관으로 용액을 부을 때는 반드시 다른 종류의 용액이 나오기 직전까지 부어야 한다. [1,1,2,3,4,1] 일 경우, 1번 용액이 맨 위에 두 겹 쌓여있으므로 용액을 부으면 [0,0,2,3,4,1] 이 되어야 한다. 즉, 그 밑의 층인 2번 용액부터는 부어서는 안된다.

3. 한 시험관에서 다른 시험관으로 용액을 부을 때, 맨 위에 서로 같은 종류의 용액이 있어야 부을 수 있다.
   즉, [0,0,1,2,4,1] 에서 [0,0,1,4,3,3] 으로 부을 수 있지만, [0,0,1,2,4,1] 에서 [0,0,3,4,1,2]로 부을 수 없다.

4. 시험관의 용량은 총 6이며, 옮겨 부을 때 넘쳐서는 안된다. 즉, [0,0,1,1,2,3] 에서 [0,1,1,3,4,5] 로 부을 수 없다. 1번 용액이 두 겹 쌓여 넘쳐 흐르기 때문이다.

5. 용액을 옮겨 붓고, 해당 시험관이 비어있는 상태면, 용액의 종류와 상관없이 부을 수 있다. 단, 위의 규칙을 준수하며 부어야 한다.

철수는 가장 적은 횟수로 용액을 옮기며 모든 시험관에 같은 종류의 용액만이 담기도록 하려 한다.

즉, [0,0,1,4,3,2], [0,0,1,2,2,3], [0,0,4,2,3,1],[0,0,3,2,1,1] 을

[0,1,1,1,1,1], [0,0,3,3,3,3], [0,2,2,2,2,2], [0,0,0,0,4,4] 이런식으로 옮기는 것이다.

이 때, 모든 시험관에 같은 종류에 용액이 담기도록 하는 가장 적은 횟수를 구하는 알고리즘을 작성하시오. 어떠한 경우에도 옮길 수 없으면 -1을 반환한다.

더 어려운 버전

이 때, 가장 적은 횟수로 모든 시험관에 같은 종류에 용액이 담기도록 하는 순서를 배열의 형태로 반환하는 알고리즘을 작성하시오. 어떠한 경우에도 옮길 수 없으면 [-1]을 반환한다.

즉, 3번째 시험관에서 5번째 시험관으로 붓고, 4번째 시험관에서 3번째 시험관으로 붓는 경우, [[3,5],[4,3]] 형식으로 반환해야 한다.

사실...

난 백준 물골드 1이라서.. 알고리즘 실력이 좋지는 않다...근데 그냥 갑자기 집 가다가 그 게임 생각이 나서 한번 만들고 싶었다. 나도 한번 시도는 해볼테니...한번 풀어보시길 바란다.