Secret of RLHF in Large Language Models Part I: PPO(Reinforcement Learning Part)

SUNGYOON LEE·2024년 6월 29일

이전 설명에 앞서 RLHF의 원리를 설명해본다.

Reinforcement Learning

RL을 LLM에 적용시키기 위해 생각해야 할 부분들이 몇 가지 있다.
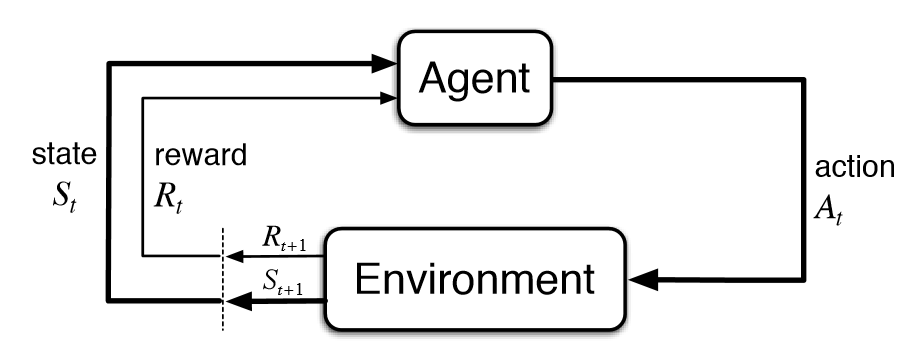
- human interaction을 environment로 간주한다.
- agent는 AI assistant로 간주한다.
- state는 dialogue history로 간주한다.
- 이러한 agent(AI assistant)는 매 타임 스텝 t마다, environment로부터 state(dialogue history)를 전달 받는다.
- 그리하여 policy $\pi$ 에 따라, AI assistant의 action $a_t$ 는 다음 스텝(다음 토큰)을 생성한다.
- 그 다음에 environment(human interaction)은 reward $r(s_t, a_t)$ 를 부여하고, 이러한 reward는 human preference data를 통해 학습된 모델로부터 산출된다.
즉, RL을 하는 목적은 optimal behavior strategy를 찾는 것이고, 이것을 달성하기 위해서는 누적 reward가 최대가 되도록 하는 것이다.

Policy Gradient Methods

Policy Gradient methods란 무엇일까?

Policy gradient methods [31] are a type of RL techniques that directly optimize the policy of the agent—the mapping of states to actions—instead of learning a value function as in value-based methods.

Policy Gradient methods란 agent(AI assistant)가 어떻게 행동해야 하는 지를 결정하는 policy(LLM model)을 최적화하는 방법이다.
이는 value-based와 대조되는 방법이라고 한다.
- 그렇다면 value-based방식과 policy gradient method의 차이점이 뭘까?
  - Value-based method -> Value function(가치 함수)를 기반으로 하여 현재 상태를 기반으로 정책을 간접적으로 최적화하는 방법론. 이 방식은 policy를 direct하게 최적화하는 것이 아닌, state-action 또는 state의 value를 학습하여 간접적으로 policy를 최적화하는 방법이다.
  - Policy gradient method -> 정책을 직접적으로 최적화하는 방법론. PPO와 같은 방법론들이 이러한 방법론임.

그렇다면 policy gradient 방식이 policy의 파라미터를 업데이트하는 방식은 어떻게 될까?

\theta \leftarrow \theta + \alpha \nabla_\theta J(\theta)

$\alpha$ 는 learning rate를 의미한다.
$J(\theta)$ 는 policy $\pi_\theta$ 를 따르는 expected return을 의미한다.
즉, $\nabla_\theta J(\theta)$ 는 특정 파라미터 $\theta$ 를 따랐을 때, 얻을 수 있는 기대보상이라고 생각하면 된다. 뭐 다르긴 하지만 누적된다는 느낌으로 gradient descent의 식에서 생각을 해보면 좋을 것 같다.

\theta \leftarrow \theta - \alpha \nabla_\theta L(\theta)

loss 식을 보면 $\nabla_\theta L(\theta)$ 는 특정 파라미터 $\theta$ 를 따랐을 때, 얻을 수 있는 loss이고, 이를 최소화하는 방향으로 파라미터를 업데이트 해주어야 하므로, 뺄셈을 해주게 된다. 반대로 gradient ascent는 expected return을 최대화하는 방향으로 파라미터를 업데이트 해주어야 하므로 덧셈을 해주게 된다.

A general form of policy gradient

\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} \left[ \sum_{t=0}^T \nabla_\theta \log \pi_\theta (a_t | s_t) \Phi_t \right]

그렇다면 policy gradient는 어떻게 정의가 될까?

$\Phi_t$ 의 값은 여러 가지가 될 수 있다.

$\Phi_t = R(\tau)$

이는 전체 에피소드 동안 얻은 누적 보상을 의미한다.
Monte Carlo 방법과 유사하게 에피소드가 끝난 후 전체 보상을 기반으로 학습하는 방법.

$\Phi_t = \sum_{t'=t}^T R(s_{t'}, a_{t'})$

이 방식은 현재 스텝 t부터 에피소드 끝까지의 누적 보상을 활용한 방법이다.
단순한 Monte Carlo에 비해서는 조금 더 효율적인 방법.

$\Phi_t = \sum_{t'=t}^T R(s_{t'}, a_{t'}) - b(s_t)$

2번 방식에 baseline $b$ 를 뺀 방법이다.
그런데 $b(s_t)$ 를 따로 구해야 하는 단점이 있다. 이러한 단점이 있는데도 불구하고 왜 굳이 구할까?
- $b(s_t)$ 는 평균이다. $s_t$ 에서 평균적으로 기대할 수 있는 보상이다. 즉 정규화 과정이라고 보면 된다.
- 보상 자체를 곧바로 $\Phi_t$ 에 더하게 되면 너무 큰 값을 더 해줄 수도 있고, 불안정하다.
- 그러나 우리가 정규화 과정을 왜 거치는가를 생각해보면 결국 안정성을 확보하기 위해서이다. 이러한 느낌과 같이 $b(s_t)$ , 즉 평균 보상을 빼주는 것이다.

그렇다면 이번에는 이러한 $\Phi_t$ 값을 왜 $\log$ 에다가 곱해주는 것일까?

$\log \pi_\theta$ 는 state $s_t$ (dialogue history)가 주어졌을 때 action $a_t$ (next token)를 생성할 확률이라고 생각하면 된다. $\Phi_t$ 는 시점 t에서의 보상에 대한 추정 값이다.

그렇다면 expected return이라는 것은 확률 x 보상의 합이라고 볼 수 있다. gradient ascent 방식을 통해서 expected return을 최대화해주는 방향으로 파라미터를 업데이트 하고자 한다면, 확률도 높아지고, 보상도 커지는 방향으로 파라미터가 업데이트되어야 한다.

이 방식으로 했을 때는 문제점이 존재한다. 위의 방식에서 말했을 때, 에피소드에서 얻는 reward를 모두 계산해야 한다. 이는 통상 Monte Carlo Sampling 방식으로 진행을 하는데, 이는 계산하기에 양도 너무 클 뿐만 아니라, 긴 에피소드의 누적 보상을 통해 계산을 하다 보니 outlier들이 계산되어 high variance가 발생한다.

※ Monte Carlo Sampling에 대해서 자세히 모르는 사람을 위해 간략히 설명하자면, 모든 에피소드를 기반으로 보상을 계산하는 방식이다.

그렇다면 high variance를 어떻게 줄일 수 있을까?

Advantage function을 사용하는 것이다.
이게 바로 위에서 말한 3번의 방식인 것이다.
Advantage function은 $A(s_t, a_t) = Q(s_t, a_t) - V(S_t)$ 로 정의된다. $V(S_t)$ 는 현재 state $S_t$ 에서의 모든 action에 대한 평균 value를 측정한 것이기 때문에, 상대적으로 1, 2번에 비해 분산을 줄일 수 있다.

Generalized Advantage Estimation

그럼 일단 3번이랑 어떻게 Advantage Function이 같은지부터 먼저 알아보자.

$Q(s_t, a_t)$ 가 무엇인가?

Q는 Action-Value Function으로 정의상으로는 특정 상태 $s_t$ 에서 행동 $a_t$ 를 했을 때, 미래에 받을 보상의 총 기대값이다.
마찬가지로 $\sum_{t'=t}^T R(s_{t'}, a_{t'})$ 도 t 시점부터 에피소드의 끝까지 받을 보상의 총 합이다.

그렇다면 이번에는 $V(S_t)$ 와 $b(s_t)$ 는 왜 같은가?

위에 말했듯이 $V(S_t)$ 는 State-Value Function으로 정의상으로는 특정 상태 t에서 정책 $\pi$ 를 따랐을 때, 평균적으로 얻을 수 있는 보상이다.
마찬가지로 $b(s_t)$ 도 $s_t$ 에서 평균적으로 기대할 수 있는 보상이다.

다시 식을 들여다 본다면,

결국 expected return을 추정하기 위해 Advantage function을 사용해야 하는데, Advantage function을 활용하기 위해서는 Q function을 활용해야 한다.
그리고 이러한 Q function을 추정하기 위해서는 실제 에피소드들로부터 return을 계산해야 하는데, 이 방법으로는 대표적으로 2가지 방법이 있다.
- Temporal Difference(TD)
- Full Monte Carlo

그런데, 첫 번째 방법인 TD를 사용하게 되면(1-step의 경우에) 상대적으로 MC방식보다 분산이 낮다. 왜냐하면 1 step마다 업데이트를 하기 때문이다. 반대로 1 step마다 업데이트를 하기 때문에 편향은 높다.
두 번째 방법인 Full Monte Carlo 방식은 TD방식 보다는 분산이 높다. 왜냐하면 에피소드의 모든 step의 보상을 사용해서 업데이트를 하기 때문이다. 반대로 모든 step의 보상을 사용해서 업데이트하기 때문에 편향은 낮다.

그렇다면 편향도 중간이고, 분산도 중간인 방법이 없나?

그것이 바로 Generalized Advantage Estimation(GAE)인 것이다.

Advantage는 직관적으로 말한다면 '내가 지금 행할 행동이 얼마나 가치가 있는 것이야?'라는 의미이다. 즉, '내가 지금 행할 행동으로 얻을 수 있는 보상이 지금 정책( $\pi)$ 을 따랐을 때 얻을 수 있는 평균적인 보상보다 얼마나 좋아?'라는 것이 핵심이다.
결국 return을 높이려면 baseline인 $V(S_t)$ 는 고정이니 $Q(s_t, a_t)$ 를 높여야 하는 것이다.
그리고 이러한 GAE 방식으로 하면 중간 정도의 bias와 중간 정도의 편향으로 비교적 정확하게 추정이 가능하다.

Proximal Policy Optimization

그렇다면 Proximal Policy Optimization(PPO)는 무엇인가?

왜 이 알고리즘이 나왔는지에 대한 배경부터 알아야 한다.
RL에서 policy를 업데이트할 때, new policy와 old policy는 기본적으로 비슷한 parameter space에 존재하게 한다.
그렇지만 parameter space 상에서 비슷한 곳에 존재한다고 해서 그럼 업데이트도 별로 없는 것이냐?라고 한다면 그것은 아니다. 업데이트는 클 수도 있다.
더군다나 parameter space 상에서 만약 멀다고 하면, model 붕괴가 일어날 수도 있다.
이를 막기 위해 Proximal Policy Optimization 방법론이 나온 것이다.
그리하여 나온 식이 우리가 대중적으로 알고 있는 RLHF의 PPO 알고리즘의 식인 것이다. $\mathcal{L}_{\text{ppo-penalty}}(\theta) = \mathbb{E}_{t} \left[ \frac{\pi_{\theta}(a_t | s_t)}{\pi_{\theta_{\text{old}}}(a_t | s_t)} \hat{A}_t \right] - \beta \text{KL}(\pi_{\theta_{\text{old}}}(\cdot | s_t), \pi_{\theta}(\cdot | s_t))$
$\frac{\pi_{\theta}(a_t | s_t)}{\pi_{\theta_{\text{old}}}(a_t | s_t)}$ 이 부분이 '현재 정책이 기존 정책과 비교했을 때 특정 행동을 선택할 확률이 얼마나 변했는지'를 나타낸다. 그래서, 정책이 많이 바뀌면 1에서 멀어질 것이고, 정책이 변하지 않으면 1에 가까울 것이다.
그리고 뒤의 KL-divergence는 RLHF를 읽어본 사람들이라면 분명히 아는 그 페널티의 영역이다. 급격하게 policy가 바뀌지 않게 해주는 term인 것이다.