드디어 딥러닝을 배워보자!
저자는 머신러닝을 먼저 공부하고 딥러닝을 배우는게 넓은 시야를 갖는 길이라고 말했지만, 나는 지금 딥러닝이 더 배우고 싶다. 하고 싶은 거 먼저 공부해야 더 빠르게 공부할 수 있겠지 ㅎㅎ 라는 마음으로 [케라스 창시자에게 배우는 딥러닝 2판]을 읽어보자 😁😁

딥러닝은 머신러닝의 하위 개념이다

질리도록 들었지만 딥러닝은 머신러닝의 하위 개념이다.
머신러닝은 3가지로 이루어진다.

• 입력 데이터 포인트: 데이터 전처리 및 가공 = 어떤 특성이 중요한가?
• 기대 출력: 라벨링 = 어떤 답을 원하는가?
• 알고리즘의 성능 측정: 학습(손실함수 값 0으로 만들기) = 얼마나 정확한가?

어떤 데이터를 넣으면 어떤 답이 나와야 하는지 알려주고, 머신러닝(ML) 모델이 가져온 해결안에 대해 평가를 하는 방식이다.

기존에 데이터와 해결안을 미리 프로그래머가 정의해두고, 새로운 데이터가 들어오면 코드를 돌리기만 하던 방식과는 다르다. 해답이 미리 주어져야 한다.

머신러닝의 역사를 뼈대만 살펴보면 아래와 같다.

• 확률적 모델링 시작: 나이브베이즈(베이즈 정리 활용), 로지스틱 회귀(분류 모델)
• 초창기 신경망 제안: LeNet
• 커널 방법: 서포트 벡터 머신(SVM) -> 특성 공학(유용한 특성만 추출)
• 결정트리, 랜덤포레스트, 그레디언트 부스팅 머신
• 발전한 신경망(딥러닝)

정말 키워드만 나열해봤다. 책에서는 더 자세히 나와있지만 나의 관심사는 딥러닝이니 저 부분은 나중에 공부하기로 마음먹고 넘어갔다.

커널 방법

커널 방법만 간단하게 소개하고 넘어가겠다. 분류 문제를 간단하게 만들기 위해서는 데이터를 고차원 표현으로 매핑하는 기법이 이론상으로는 좋아 보이지만 실제로는 컴퓨터로 구현하기 어려운 경우가 많다. 그래서 커널 기법이 등장했다. 새로운 공간에서의 두 데이터 포인트 사이의 거리를 계산만 할 수 있다면, 굳이 새로운 공간의 좌표 자체를 구할 필요가 없다. 커널 함수는 두 포인트 사이의 거리를 효율적으로 계산하는 함수다. (나중에 공부 ^^)

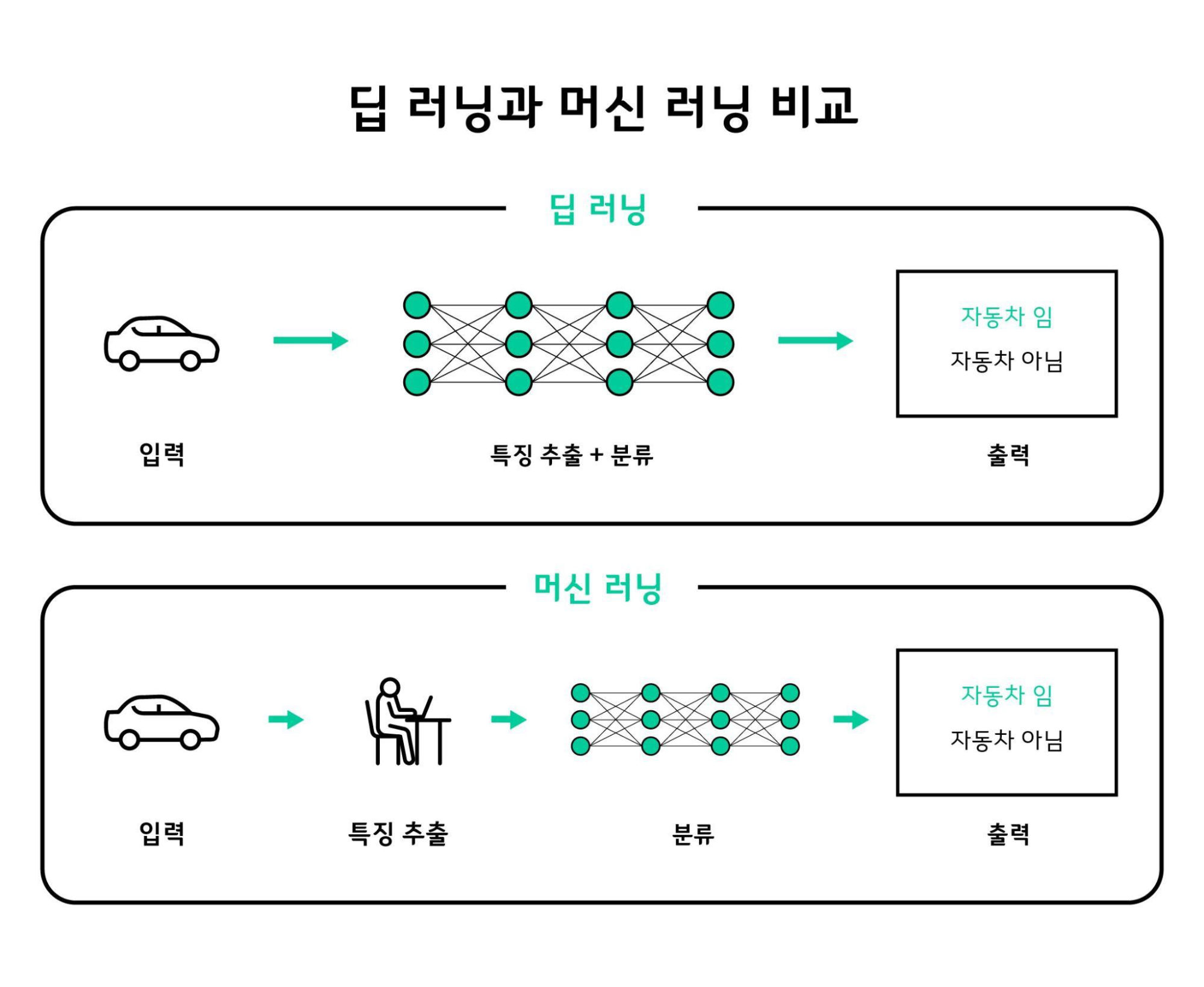
딥러닝은 신경망 레이어를 깊게(Deep) 연결한 머신러닝 모델이다. 위 그림에서 보면 딥러닝에서는 특징 추출 부분이 분류와 합쳐졌다. 서포트 벡터 머신은 좋은 성능을 가졌지만 올바른 특성을 일일이 떠먹여줘야하는 수고가 있었다. 예를 들면 손글씨 숫자를 분류할 때 원시 픽셀 값을 사용할 수는 없다. 픽셀 히스토그램처럼 문제를 쉽게 만드는 유용한 표현을 수동으로 먼저 찾아야한다. 이런 작업을 특성 공학이라고 한다. 딥러닝은 이런 특성을 알아서 찾아낸다. 책에서 마음에 들었던 비유가 있다.

빨간색 종이와 파란색 종이 두개를 마구 구겨서 공으로 만들어냈다고 해보자. 이 공을 다시 빨간색과 파란색 종이로 다시 분리하려면, 조금씩 종이를 살살 펼칠 것이다. 아무리 꼬여있는 데이터라 하더라도 거기서 최대한 올바른 정보를 추출해낸다. 물론 그럼에도 아무런 의미가 없다면 Garbage-In-Grabage-Out일 것이다.

이런 딥러닝이 발전할 수 있는 이유라면 3가지다.

• 하드웨어의 발전
• 데이터의 축적
• 알고리즘: 병렬 연산, 활성화 함수, 가중치 초기화, 옵티마이저 등

신경망의 수학적 이해

물론 여기서 수식을 엄청나게 이해하지는 못했다. 간단하게 훑어본 기분으로 넘어가보자.
우선 케라스로 구현한 간단한 신경망 코드를 살펴보자.

from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.datasets import mnist # 기본적인 손글씨 판별 데이터셋 MNIST import

model = keras.Sequential([
	layers.Dense(512, activation="relu") # relu로 비선형 함수 만들기, 512차원 layer 하나
    layers.Dense(10, activation="softmax") # softmax로 10개의 class에 각각 확률 값 계산하기 -> 0~9까지 숫자 예측
])

model.compile(
	optimizer="rmsprop", # 최적화함수 (역전파 기법)
    loss = "sparse_categorical_crossentropy", # 손실함수
    metrics = ["accuracy"] # 정확도 지표만 고려해서 훈련과 테스트 과정 모니터링
)

train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((60000, 28 * 28))
test_images = test_images.astype("float32") / 255

model.fit(train_images, train_labels, epochs=5, batch_size=128)

일단 완성체를 한번 지르고 하나씩 코드를 뜯어보자.

텐서 연산

keras.layers.Dense(512, activation="relu")

for output in range(512):
	output = relu(dot(W, input) + b)

위 두 코드는 같은 결과를 갖는다.
딥러닝에서 위와 같은 layer를 겹겹이 쌓아 수천만 그 이상의 output 계산이 생긴다. 이를 선형으로 하나씩 계산하면 시간이 많이 걸린다. 병렬 계산을 위해 Numpy가 필요하다. Numpy는 BLAS(Basic Linear Algebra Subprogram)을 매우 효율적이고 저수준의 텐서 조작으로 구현해놓았다. 포트란이나 C언어로 구현되어있다. 케라스는 넘파이 기반으로 병렬 연산을 지원한다.

브로드 캐스팅

큰 텐서와 작은 텐서를 연산할 때 작은 텐서의 차원을 큰 텐서에 맞춰줘야 한다. 이 작업을 브로드 캐스팅(broadcasting)이라고 부른다.

X -> (32, 10) 행렬
y -> (10, ) 벡터

위 두 텐서를 연산하려면 두 가지 과정을 거친다.

1. 큰 텐서의 ndim에 맞도록 작은 텐서에 브로딩캐스팅 축이 추가된다.
2. 작은 텐서가 새 축을 따라서 큰 텐서의 크기에 맞도록 반복된다.

코드로 보면 다음과 같다.

y = np,expand_dims(y, axis=0) # y에 브로드캐스팅 축 추가 -> y의 크기가 (1, 10)이 됨
Y = np.concatenate([y] * 32, axis=0) # 축 0을 따라 y를 32번 반복하여 크기가 (32,10)인 Y를 얻음

행렬로 이해하면 행마다 똑같은 열을 32번 복사한 행렬을 만든 것이다. 정말 계산의 편의를 위한 작업이다.

점곱

텐서 곱셈(tensor product) 또는 점곱(dot product)라고 불리는 연산은 가장 널리 사용되고 유용한 텐서 연산이다.

output = relu(dot(W, input) + b)

여기서 dot이 점곱이다. 이름이 점곱인 이름은 수학 기호가 점이다.

z = x ⋅ y

점곱은 어떻게 하는가?
이 책은 참 특이한게 설명이 수식보다는 코드다. 이 글에서도 코드로 간다.

for i in range(x.shape[0]):
	z += x[i] * y[i]

for 문으로 이해하기 좋다. 4차원 텐서는 4중 for문이고 5차원 텐서는 5중 for문일 것이다.
x 와 y 두 행렬이 있을 때 이렇게 계산한다. 그림으로 보자.

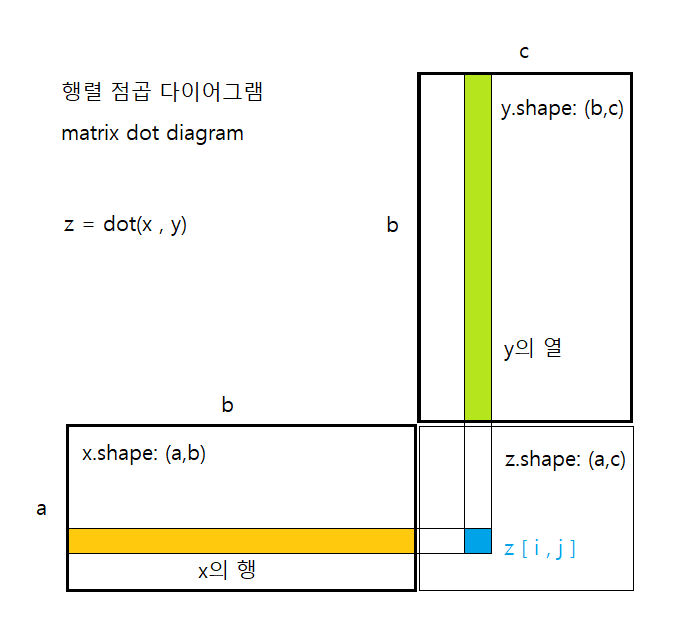
수식은 이렇다.

텐서의 형태로 보면 아래와 같다. 마지막 차원과 첫번째 차원이 맞물린다.

(a, b, c, d) ⋅ (d, e) = (a, b, c, e)

텐서 크기 변환

x = np.array([
	[0., 1.],
	[2., 3.],
	[4., 5.]
])
x.shape # (3, 2)
x.reshape((2, 3))

>>> #reshape 결과
x = 
[[0., 1., 2.],
[3., 4., 5.]]

텐서의 크기를 변환한다는 것은 특정 크기에 맞게 열과 행을 재배열한다는 뜻이다.

x = np.array([
	[0., 1.],
	[2., 3.],
	[4., 5.]
])
x = np.transpose(x)

>>> #transpose == 전치 결과
x = 
[[[0., 2., 4.],
[1., 3., 5.]]

전치는 행과 열을 바꾸는 연산이다. 그냥 reshape하는 것과 모양이 조금 다르다.

텐서 연산의 기하학적 해석

이동, 회전, 크기변형, 선형변환, 아핀변환, relu 활성화 함수를 사용하는 Dense층 등의 내용이 들어있다.

.. 수식 쓰기가 너무 귀찮았다.

딥러닝의 기하학적 해석은 여기서도 종이 구겼다 펼치는 예시가 적용된다.

경사하강법

신경망의 모든 함수 (변환)은 미분가능한 수식이다.
텐서 함수의 도함수 == 그레디언트(gradient)

y_pred = dot(W, x) # W = 가중치, x = 입력 데이터
loss_value = loss(y_pred, y_true) # y_pred는 예측 값, y_true는 라벨

위 수식에서 x, y_true는 상수다. 그러므로 다음 수식은

loss_value = f(w)

라고 할 수 있다. 여기서는 도함수를

grad(loss_value, W)

로 표현한다.

연쇄 법칙 (chain rule)

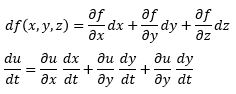
자세한 설명은 생략한다..ㅎ

계산 그래프를 활용한 자동 미분

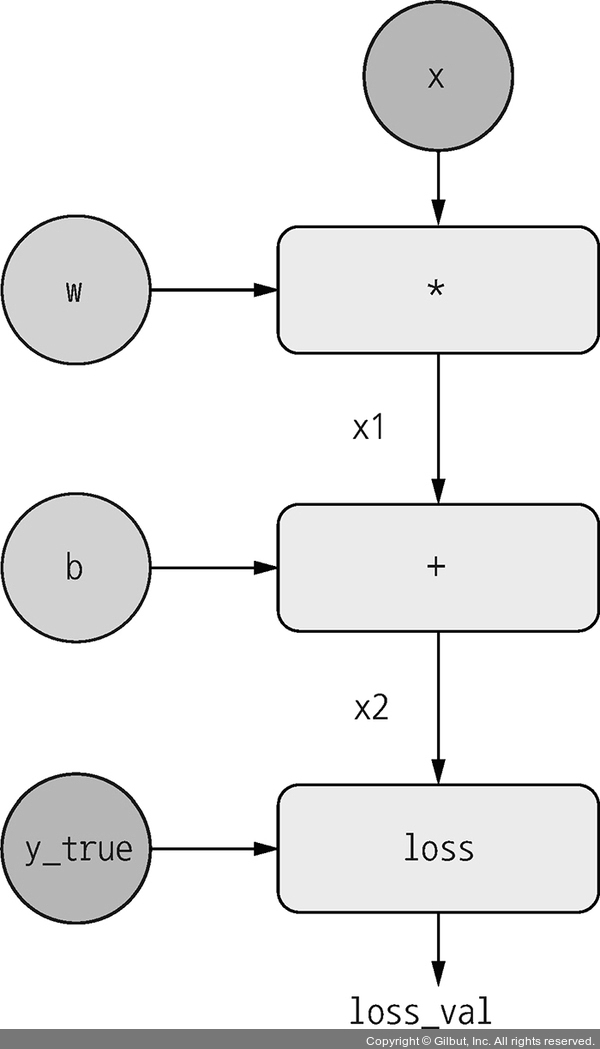
계산 그래프로 표현하고 이를 분산(병렬)처리할 수 있다는 개념을 알아갔다.
계산 과정을 도표로 작성 및 동일 계산을 "분산"해서 병렬 처리하는 코드? tensorflow에 탑재되어있다. GradientTape라고 부른다. 나중에 공부해볼 수도 있겠다.

계산 그래프를 활용하니 순방향, 역전파 설명이 더 잘 되었다. 나중에 설명할 일 생기면 써먹자.

끝