참고한 책: 케라스 창시자에게 배우는 딥러닝 2판

케라스(Keras)는 최고(Best)다.

지난 글에서 정리한 1~2장은 수학적 배경지식과 딥러닝에 대한 설명이었다면 3장에서는 텐서플로우와 케라스에 대한 이해도를 높일 수 있었다. 이 장을 읽으면서 단순히 케라스의 모델을 import해서 쓰는게 아니라 케라스가 어떻게 동작하는지, tensorflow로 단순한 케라스 객체를 따라 만들어보며 이해할 수 있었다.

케라스를 만든 이 책의 저자는 얼마나 이론을 깊게 이해하고 또 구현 능력을 갖춘 것일까? 나도 열심히 공부해서 케라스나 텐서플로우 같은 대형 프레임워크의 컨트리뷰터로 활동하고 싶다. 그 날을 위해 오늘도 열심히 공부하자!

텐서플로우 (TensorFlow)

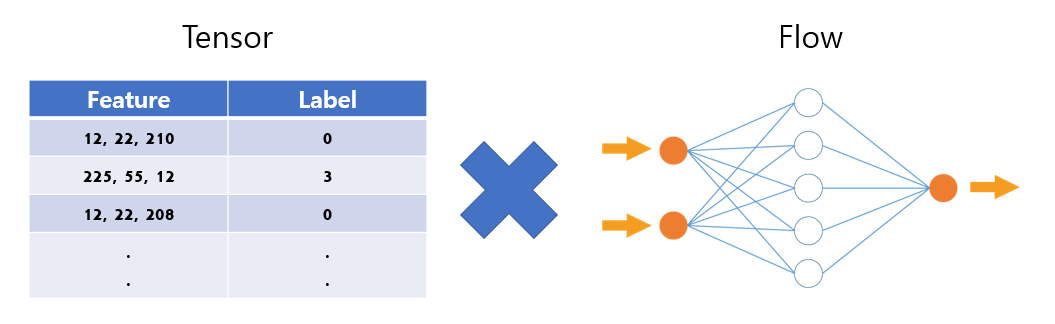
텐서플로우는 넘파이처럼 수치를 나타내기 위한 라이브러리다. 넘파이처럼 빠른 병렬 연산이 가능하다. 그럼 넘파이와 차이점은 무엇일까?

• 미분 가능한 식을 넣으면 자동으로 Gradient를 계산해주는 "GradientTape" 기능이 있다.
• GPU와 TPU에서 실행할 수 있다.
• 연산을 분산하기 쉽다. (tf로 정의한 식을 분산 연산한다.)
• 배포가 쉽다.

---

텐서플로우 연산

텐서플로우에서 사용하는 기본 연산을 알아보자.
기본적인 연산 예제와 주석을 달아두었다. 간편하게 복습하기 좋다.

import tensorflow as tf

a = tf.zeros(shape=(2, 1)) 	# (2, 1) 행렬을 만들고 0으로 채움
b = tf.ones(shape=(2, 1)) 	# (2, 1) 행렬을 만들고 1로 채움

c = tf.Variable(3.) # 변수
d = tf.constant(3.) # 상수

e = tf.random.normal(shape=(3,1), mean=0, stddev=1)  # 평균 0, 표준편차 1 정규분포에서 (3, 1) 행렬 뽑음
f = tf.random.uniform(shape=(3,1), minval=0, maxval=1) # 0~1 균등분포에서 (3, 1) 행렬 뽑음

tf.~ 식으로 쉽게 행렬을 만들 수 있다. 0으로 채우기, 1로 채우기, 정규분포로 채우기, 균등분포로 채우기 등 다양한 데이터를 만들 수 있다. 변수는 tf.Variable()로 첫번 째 문자가 대문자이다!

a = tf.Variable(a)
a.assign(tf.ones(((2,1)))) 	# numpy와 다르게 tf는 object형태라 assign 메소드로 따로 할당
a[0,0].assign(3.) 			# 개별 할당 가능
a.assign_add(a) 	# +=
a.assign_sub(a) 	# -=
a = tf.square(a)  	# 제곱
a = tf.sqrt(a)    	# 제곱근
b = tf.transpose(a)	# 전치
e = tf.matmul(a, b) # 점곱
e *= e            	# 원소별 곱셈

tf는 변수와 상수 모두 tf 객체로 만들기 때문에 assign 메소드로 값을 할당해야 한다. 인덱싱 기능을 제공해서 행렬 원소만 할당할 수 있다.

# GradientTape는 미분 가능한 식을 넣으면 자동미분해준다.
# 아래는 위치, 속도, 가속도 예제이다.

time = tf.Variable(0.)
with tf.GradientTape() as outer_tape:
  with tf.GradientTape() as inner_tape:
    position = 4.9 * time ** 2
  speed = inner_tape.gradient(position, time)
acceleration = outer_tape.gradient(speed, time)

위는 GradienTape를 활용한 속도, 가속도 구하기 예제이다. with ~ tape: 안에 수식을 넣고 밖에서 tape의 gradient(미분값)을 구할 수 있다.

수식은 미분 가능해야 한다. 수식의 tf 변수 객체만 미분 값을 제공하므로 timed을 tf.constant()로 지정하면 미분이 되질 않는다.

케라스 대신 텐서플로우로 딥러닝 모델을 구현해보면 깊이 공부한 건 줄 알았는데, 텐서플로우 안에 들어있는 수식 함수들과 C언어 연산이라는 심해를 보았다. GradientTape 안에 들어있는 함수를 만들 수 있는 사람은 얼마나 될까? 경쟁력은 이런 기초에서 나오는 것이다! 정말이지 공부할 건 넘쳐나는 것 같다. 우선 텐서플로우와 수학적 원리를 조금씩 이해해보자! 라는 마음으로 책을 읽었다.

텐서플로우로 선형분류기 구현하기

그럼 이제 본격적으로 텐서플로우를 활용해 선형분류기를 만들자!
선형분류기는 케라스의 기본적인 객체 중 하나이다. 일반적인 레이어 하나가 선형분류기라고 보면 된다. 물론 층을 쌓을 수록 활성화함수를 거쳐 비선형이 된다. 여기서는 하나의 레이어가 어떻게 구성되어있는지 텐서플로우로 구현하며 이해하겠다.

import numpy as np

num_samples_per_class = 1000
negative_samples = np.random.multivariate_normal(
    mean=[0, 3],				# 평균
    cov=[[1, 0.5], [0.5, 1]],	# 공분산
    size=num_samples_per_class	# 데이터 개수
)
positive_samples = np.random.multivariate_normal(
    mean=[3, 0],
    cov=[[1, 0.5], [0.5, 1]],
    size=num_samples_per_class
)

우선 임의의 데이터를 만든다. 두 개의 집단을 만들고 집단 당 데이터는 1000개씩 만든다. 각 집단은 두 개의 특성을 갖고있다 (x축 y축으로 통칭). negative_samples는 정규분포에서 뽑으며 평균, 공분산, 자료의 개수를 지정해주었다. positive_samples도 마찬가지다.

inputs = np.vstack((negative_samples, positive_samples)).astype(np.float32)
targets = np.vstack((np.zeros((num_samples_per_class, 1), dtype="float32"),
                   np.ones((num_samples_per_class, 1), dtype="float32")))

inputs에 두 자료를 뭉쳐놓고, targets에서 0과 1로 라벨링을 해준다.

import matplotlib.pyplot as plt

plt.scatter(inputs[:, 0], inputs[:, 1], c=targets[:, 0])
plt.show()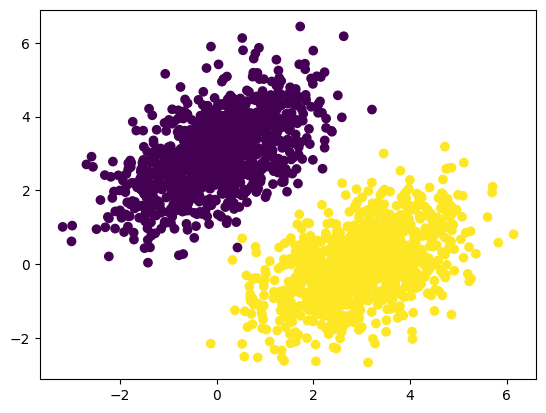

plt.scatter( )에서 c 옵션을 target[ : , 0 ], 즉 라벨 번호로 지정해준다. c 옵션의 활용법을 배웠다.

input_dim = 2	# 특성 2개
output_dim = 1	# 결과는 Class 분류

W = tf.Variable(initial_value=tf.random.uniform(shape=(input_dim, output_dim)))
b = tf.Variable(initial_value=tf.zeros(shape=(output_dim,)))

W는 initial_value의 shape가 (2, 1)이다. x축과 y축 각각의 특성에 대한 W1, W2가 필요하기 때문이다. 반면 b는 (1, )로 하나만 붙는다.

# 선형 분류기
def model(inputs):
  return tf.matmul(inputs, W) + b

정방향 패스의 연산을 반환한다. inputs의 shape은 (1000, 2) W는 (2, 1)이므로 점곱을 하면 (1000, 1)이 된다. 이후 b를 더해준다.

# 손실함수
def square_loss(targets, predictions):
  per_sample_losses = tf.square(targets - predictions)
  return tf.reduce_mean(per_sample_losses)

손실함수는 target과 prediction의 오차를 계산해 제곱한다. 여기서 target은 0 또는 1 뿐이다. model은 앞서 만든 선형 분류기이므로 랜덤이다. tf.reduce_mean( ) 함수가 모든 loss의 평균을 Scala값으로 만들어준다.

learning_rate = 0.1

def training_step(inputs, targets):
  with tf.GradientTape() as tape:
    predictions = model(inputs)
    loss = square_loss(targets, predictions)
  grad_loss_wrt_W, grad_loss_wrt_b = tape.gradient(loss, [W, b])
  W.assign_sub(grad_loss_wrt_W * learning_rate)
  b.assign_sub(grad_loss_wrt_b * learning_rate)
  return loss

GradientTape( )를 이용해서 loss에 대한 W와 b의 편미분값을 계산한다. loss를 최대한 줄이는게 목적이다.

for step in range(40):
  loss = training_step(inputs, targets)
  print(f"{step} 번째 스텝의 손실: {loss:.4f}")

0 번째 스텝의 손실: 2.1274
1 번째 스텝의 손실: 0.2540
2 번째 스텝의 손실: 0.1287
3 번째 스텝의 손실: 0.1079 
...
37 번째 스텝의 손실: 0.0276
38 번째 스텝의 손실: 0.0273
39 번째 스텝의 손실: 0.0270

40번 학습시킨다. 여기서는 게산의 편의를 위해 전체 데이터를 계속 학습했지만, 데이터가 커지면 미니배치 경사하강법으로 학습을 시키는게 일반적이다.

predictions = model(inputs)
plt.scatter(inputs[:, 0], inputs[:, 1], c=predictions[:, 0] > 0.5)
plt.show()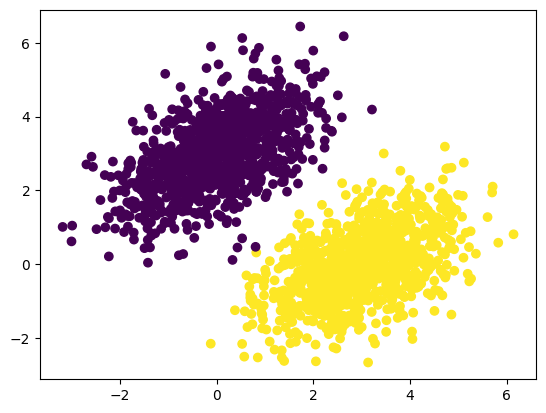

잘 분류해낸 모습이다. 위의 원래 데이터에서 특이값(보라색이지만 노란 집단에 가까움)은 잡아내지 못했다. 선형분류기의 한계이다. 딥러닝은 직선이 아니라 고차원의 기준을 만들어내므로 특이값에 대한 분류가 더 용이할 것이다. 물론 여기서는 데이터가 너무 깔끔해서 그럴 필요는 없어보인다.

x = np.linspace(-1, 4, 100)
y = - W[0] / W[1] * x + (0.5 - b) / W[1]	# x * W[0] + y * W[1] + b = 0.5 식 이항
plt.plot(x, y, "-r")
plt.scatter(inputs[:, 0], inputs[:, 1], c=predictions[:, 0] > 0.5)
plt.show()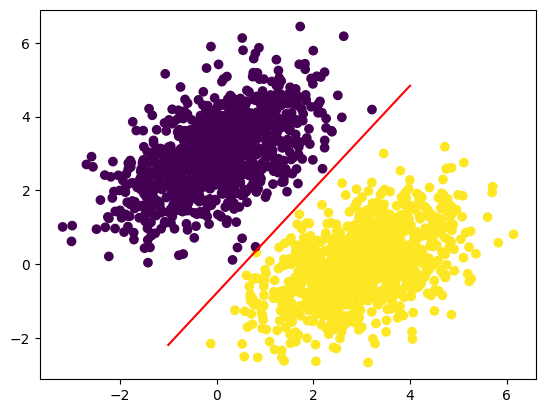

x * W[0] + y * W[1] + b = 0.5	#prediction의 예측 값. 0.5 미만이면 class 0, 초과면 class 1 이다.

선형분류기의 기준선을 그려보았다. x축 [-1, 4] 범위에 점을 100개 찍어서 선을 만든다. 이에 대응하는 y축 값들을 계산하여 plot한다. 이 기준선이 선형분류기가 데이터의 클래스를 판별하는 기준이다.

선형분류기 객체로 만들기

class SimpleDense(keras.layers.Layer):	# keras.layers.Layer 상속
  def __init__(self, units, activation=None):
    super().__init__()
    self.units = units					# 출력 차원의 크기
    self.activation = activation		# 활성화함수

  def build(self, input_shape):
    input_dim = input_shape[-1]			
    self.W = self.add_weight(shape=(input_dim, self.units), initializer="random_normal")
    self.b = self.add_weight(shape=(self.units, ), initializer="zeros")

  def call(self, inputs):
    y = tf.matmul(inputs, self.W) + self.b
    if self.activation is not None:
      y = self.activation(y)
    return y

# keras.layers.Layer class의 __call__ 메소드
def __call__(self, inputs):
	if not self.built:
		self.build(inputs.shape)
		self.built = True
    return self.call(inputs)

앞서 살펴본 선형 분류기를 객체로 만든다면 이런 모습일 것이다.
만약 keras.layers.Layer class를 상속하지 않고 __call__() 함수에서 직접 build했다면 input_dim을 파라미터로 받아야 한다. 수동적으로 파라미터를 받지 않고 동적으로 input_dim을 추론하기 위해 call과 build 메소드를 따로 만든 것이다.

케라스 (Keras)

그럼 케라스는 무엇인가?

• TensorFlow 기반 딥러닝 프레임워크
• 텐서플로우에서 한단계 더 나아간 사람 친화적 프레임워크!

텐서플로우로 선형분류기를 구현해보았다. 그 다음에 케라스를 이용한다면? 훨씬 편하다!
케라스를 사용해서 앞서 만든 선형분류기를 구현해보자.

케라스로 선형분류기 구현하기

from tensorflow.keras import layers
layer = layers.Dense(32, activation="relu")

케라스는 레이어가 이미 구현되어 객체로 포장되어 있다. layers.Dense가 앞서 만든 SimpleDense와 유사한 구조를 갖고 있다. 물론 더 다양한 기능들이 포함되어 있다. 오픈소스 코드에 들어가서 코드를 뜯어보는 것도 재밌는 작업일 것 같다.

from tensorflow.keras import models
from tensorflow.keras import layers

model = models.Sequential([
    layers.Dense(32, activation="relu"),
    layers.Dense(32)
])

Sequential을 통해 여러 레이어를 블록 쌓듯이 연결한다.

신경망 설계에 필요한 것들

가설공간 정의하기

신경망을 설계할 때 가설공간을 정의하는 직관은 매우 중요하다. 이 직관은 튼튼한 기초 지식과 경험에서 나온다. 엔지니어의 진짜 실력 중 하나라고 말할 수 있다. 예를 들면 위에서 두 개의 집단이 선형으로 충분히 분류가 가능하다고 판단하면 단순히 선형분류기(아핀 변환)으로 해결이 가능하다. 하지만 데이터의 분포가 복잡해질 수록 적합한 신경망 모델의 설계가 중요해진다.

손실함수 (=목적함수)

손실함수는 최소화할 값을 의미한다. 책에 재밌는 예가 나온다. 만약 인공지능에게 "인류의 평균 행복지수 높이기"라는 목적을 갖고 손실함수로 인류의 평균 행복지수를 설정하면 어떻게 될까? 행복한 인간을 제외한 모든 인간을 사살한다는 답을 도출할 수도 있다. 손실함수를 어떻게 섬세하게 설정하느냐에 따라 인공지능의 결과가 만족스러울 수도 있고, 불만족스러울 수도 있다. 아래는 대표적인 손실함수 모델 리스트다.

CategoricalCrossentropy,
SparseCategoricalCrossentropy,
BinaryCrossentopy,
MeanSquareError,
KLDivergence,
CosineSimilarity,
...

옵티마이저

옵티마이저는 손실함수를 업데이트하는 방법이다. 기본적으로 신경망은 확률적 경사하강법(Stochastic Gradient descent)의 발전된 모델들을 많이 사용한다. 이전 포스트에서 정리한 모멘텀(Momentum) 개념 등 다양한 개선 모델이 있다. 아래는 대표적인 옵티마이저 리스트다.

SGD,
RMSprop,
Adam,
Adagrad,
...

측정 지표

측정 지표는 훈련 과정에서 모니터링할 성공의 척도다. 손실함수는 항상 0에 수렴하도록 작동한다. 측정 지표는 분류가 얼마나 정확히 되었는지 퍼센트로 표시하는 등의 역할을 한다. 측정 지표는 모델 최적화에 직접 관여하는게 아니라 모니터링 용도이므로 미분 가능하지 않아도 된다.

CategoricalAccuracy,
SparseCategoricalAccuracy,
BinaryAccuraccy,
AUC,
Precision,
Recall

케라스 메서드

케라스 모델에는 여러 메서드가 있다. 알아보자.

model.compile( )

메서드 훈련 과정을 설명하는 메서드다.

model.compile(
	optimizer="rmsprop",
    loss="meann_squared_error",
    metrics=["accuracy"]
)

model.fit( )

메서드 훈련 루프를 설명하는 메서드다.

history = model.fit(
	inputs,
    targets,
    epochs=5,
    batch_size=128,
    validation_data=(val_inputs, val_targets)
)

validation = model.evaluate()

model.predict( )

예측 값을 반환하는 메서드다. 그냥 model()로 전체 예측 값을 출력해도 되지만 한번에 병렬로 출력하려면 GPU에 부담이 갈 수 있다. predict 메서드는 batch_size로 계산하기 때문에 부담이 덜하다.

정리하며

그냥 모델 임포트해서 쓰는 것보다 이렇게 하나씩 텐서플로우로 만들고 이해하려 하니까 더 공부한 느낌이 든다. 나중에 나도 저런 모델을 직접 연구할 날이 올 것이다. 그 때를 위해 꾸준히 공부하자!

끝