✅ 문제 풀이 (Dynamic Programming)
큰 문제를 작은 문제로 나누어푸는 알고리즘의 종류
1. Overlapping Subproblem (겹치는 부분문제)
2. Optimal Substructure (최적 부분 구조)풀이 방식은 다음과 같다.
1. Bottom-Up : 최초값부터 시작해 Tabluation 방식으로 계산
(어떠한 입력이 들어와도 처음 계산이 필수적이므로 불필요한 연산 발생)
2. Top-Down : 이전 계산 값을 memoization 하여 매번 실행 없이 계산하여 실행속도를 높이는 기법 (재귀의 호출 스택이 recursion error를 발생시킬 수 있어 limit 필요)
🎈 2839 설탕 배달
설탕 무게가 주어지고, 3kg, 5kg 봉지로만 배송이 가능할 때 최소 봉지 개수를 출력하는 문제, 해결이 안되면 -1을 출력하는 문제
import sys
input = sys.stdin.readline
n = int(input())
answer = 0
while n >= 0:
if n % 5 == 0:
answer += (n//5)
print(answer)
break
n -= 3
answer += 1
else:
print(-1)< 풀이 과정 >
3kg 보다 5kg가 더 크므로 Top-down 방식으로 주어진 설탕무게 n이 5로 나누어지면 정답은 5로 나눈 몫을 출력하고, 3kg씩 빼면서 확인해준다. 만일, 반복해서 n이 0보다 작아지면 -1을 출력한다.
🎈 11726 2xn 타일링
n이 주어지고, 2xn크기의 직사각형을 1x2, 2x1타일로 채우는 방법의 수를 구하는 문제
import sys
input = sys.stdin.readline
n = int(input())
dp = [0 for _ in range(n+1)]
if n <= 3:
print(n)
else:
dp[1] = 1
dp[2] = 2
for i in range(3, n+1):
dp[i] = dp[i-2] + dp[i-1]
print(dp[n] % 10007)< 풀이 과정 >
n = 1부터 4까지 그림을 직접 그려보며 구현하니, 피보나치 수열을 따르는 문제
1 부터 시작해 n까지의 리스트 내 값을 직접 미리 만들어놓은 후 주어진 n의 값을 10007로 나눈 나머지를 리턴하는 문제
🎈 1149 RGB 거리
n개의 집이 주어지고 n줄 만큼의 빨강, 초록, 파랑으로 칠하는 비용이 주어진다. 각 집을 칠하면서 이전, 이후 집과 다른 색을 칠하려 할 때 모든 집을 칠하는 최소 비용을 구하는 문제.
import sys
input = sys.stdin.readline
n = int(input())
graph = []
for _ in range(n):
graph.append(list(map(int, input().split())))
for i in range(1, n):
graph[i][0] = min(graph[i-1][1], graph[i-1][2]) + graph[i][0]
graph[i][1] = min(graph[i-1][0], graph[i-1][2]) + graph[i][1]
graph[i][2] = min(graph[i-1][0], graph[i-1][0]) + graph[i][2]
print(min(graph[n-1]))
< 풀이 과정 >
n을 입력받고 n줄만큼의 비용이 주어진 숫자들을 graph리스트에 집어넣는다
그 이후, 그래프를 활용하여 아래줄로 내려갈수록 현재 집의 비용 = 이전 줄의 다른색깔 집 2개 중 최소 + 현재 값으로 갱신해가며 마지막줄의 최소 값을 출력하는 형태로 구현하였다.
🎈 11727 2xn 타일링 2
n이 주어지고 2xn 직사각형을 1x2, 2x1, 2x2 사각형의 타일로 채우는 방법의 수를 리턴하는 문제
import sys
input = sys.stdin.readline
n = int(input())
dp = [0] * (n+1)
dp[0] = 0
dp[1] = 1
dp[2] = 3
for i in range(3, n+1):
dp[i] = dp[i-2] * 2 + dp[i-1]
print(dp[n]%10007)< 풀이 과정 >
1~4까지의 n을 살펴보니, 현재 타일 수는 이전 타일 수 + 2번 이전의 타일 수 * 2임을 알 수 있다. 이를 dp 그대로 구현한 문제
🎈 12865 평범한 배낭
여행에 필요한 물건 n개가 있고, 각 물건은 무게 w와 가치 v를 갖는다. 배낭에는 최대 무게k만큼 버틸 수 있을 때 넣을 수 있는 물건의 최대 가치합을 구하는 문제
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
# 물건 개수 X 담을 수 있는 무게로 그래프 생성
bag = [[0]*(k+1) for _ in range(n+1)]
for i in range(1, n+1):
w, v = map(int, input().split())
for j in range(1, k+1):
# 담을 수 있는 무게보다 현재 물건의 무게가 무겁다면 이전 물건 가방 무게 값 유지
if j < w:
bag[i][j] = bag[i-1][j]
# 담을 수 있는 무게가 더 가볍다면 이전 물건 가방무게값 vs 이전물건 가방무게 - 물건 무게 값 비교
else:
bag[i][j] = max(bag[i-1][j], bag[i-1][j-w] + v)
print(bag[n][k])< 풀이 과정 >
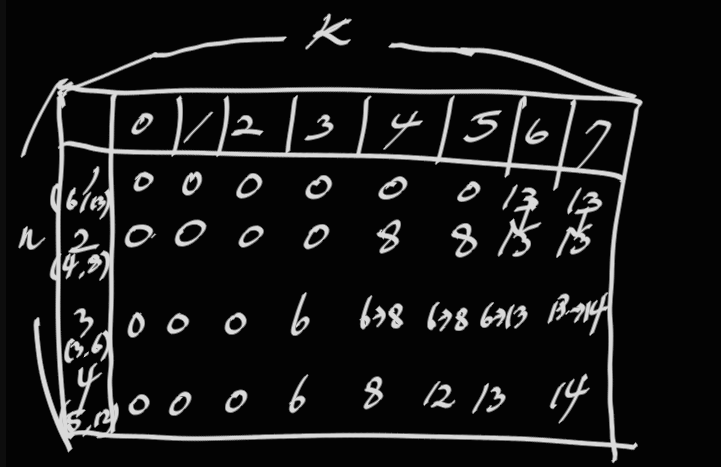물건 개수 n과 배낭에 담을 수 있는 무게 값 k를 입력받아 for문으로 우선 n줄 만큼의 물건의 [무게, 가치] 을 w,v 변수로 저장한다.
앞서 bag이라는 변수로 물건 개수 X 담을 수 있는 무게를 표현한 2차원 그래프를 만들어주고 각 위치의 데이터 값은 가치로 표현해준다. 위 그림을 보면 좀 더 이해하기 쉽다.
따라서 조건문은 다음과 같이 작성할 수 있다.
1) 담을 수 있는 무게가 현재 배낭에 넣으려는 물건의 무게가 더 무겁다면,
bag 2차원 배열의 현재 값은 [이전 물건][현재 가방 무게]를 유지한다.
2) 현재 배낭에 넣으려는 물건보다 담을 수 있는 무게가 더 크면,
bag 2차원 배열의 현재값은 [이전물건][현재가방무게] vs [이전물건][가방무게-현재 넣으려는 물건 무게] + 가치를 따져서 처리한다.
🎈 1010 다리놓기
서쪽엔 n개의 사이트, 동쪽엔 m개의 사이트가 있고 서쪽 사이트와 동쪽 사이트를 연결하려 한다. 한 사이트에는 최대 한 개의 다리만 지을 수 있고 다리끼리는 서로 겹칠 수 없을 때 다리를 지을 수 있는 최대 경우의 수를 구하는 문제
import sys
input = sys.stdin.readline
t = int(input())
for _ in range(t):
n, m = map(int, input().split())
dp = [[0]*(m+1) for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, m+1):
if i == 1:
dp[i][j] = j
continue
if i == j:
dp[i][j] = 1
else:
if j > i:
dp[i][j] = dp[i][j-1] + dp[i-1][j-1]
print(dp[n][m])< 풀이 과정 >
Combination을 이용하여 수리적으로 구현한 문제.
dp로 2차원 리스트를 (n+1)x(m+1)크기로 만들어준다. 그 이후 combination을 보면 다음과 같다.
nCn = 1, nC1 = n, nCk = n-1Ck + n-1Ck-1 이므로, 이를 2중 for문 이후 i, j인덱스를 이용하여 구현하였다.
🎈 2193 이친수
0과 1로만 이루어진 수는 이진수라 부르고 이진수들 중 이친수는 다음과 같은 성질을 만족한다.
1. 이친수는 0으로 시작하지 않는다.
2. 이친수에서 1이 2번 연속으로 나타나지 않는다.
n이 주어지고 n자리 이친수의 개수를 구하는 문제.
import sys
input = sys.stdin.readline
n = int(input())
dp = [0, 1, 1]
for i in range(3, n+1):
dp.append(dp[i-2] + dp[i-1])
print(dp[n])< 풀이 과정 >
n자리 이진수들을 직접 만들어보면 피보나치 수열을 따르는 것을 확인할 수 있다.
ex) n = 1 : 1 // n = 2 : 10 // n = 3 : 100, 101 // n = 4 : 1000, 1001, 1010 으로 개수가 늘어남을 알 수 있다.
따라서, 이를 dp로 [0, 1, 1]로 미리 만든 후 3부터 n까지의 값은 for문으로 append하여 구현하였다.
🎈 14501 퇴사
퇴사까지 n+1일 남고, 남은 n일 동안 최대한 많은 일을 하려고 한다. 각 업무는 완료하는데 소요되는 기간 T와 받을 수 있는 금액 P로 구성되어 있을 때 최대 수익을 구하는 문제.
제한 조건은 한 업무를 진행하면 다른 업무는 진행할 수 없다는 것이 특징이다.
import sys
input = sys.stdin.readline
n = int(input())
income = [0]*(n+1)
plan = []
for _ in range(n):
plan.append(list(map(int, input().split())))
for i in range(n):
for j in range(i+plan[i][0], n+1):
if income[j] < income[i] + plan[i][1]:
income[j] = income[i] + plan[i][1]
print(income[-1])< 풀이 과정 >
income으로 dp 구현을 위해 0으로 리스트를 만들고, for문을 돌며 T, P를 리스트로 plan에 저장한다. 그 이후 반복문을 돌리는데 다음과 같다.
i : i번째 날짜까지 일할 때 얻는 수익
j : i번째 날짜에 업무를 시작할 때, i+업무끝나는 기간 ~ n으로 즉, 남은 날짜 중 업무가 가능한 날짜를 의미한다.
이후, j번째 날짜의 수익이 이전날짜 수익 + 업무를 하여 얻은 수익보다 작다면 update하는 식으로 처리한다.
🎈 9251 LCS
LCS(Longest Common Subsequence) 최장 공통 부분 수열 문제는 두 수열이 주어졌을 때 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제로 예제는 다음과 같다.
ACAYKP // CAPCAK의 LCS는 ACAK가 되고 결과는 LCS의 길이를 출력한다.
import sys
input = sys.stdin.readline
seq1 = input().strip().upper()
seq2 = input().strip().upper()
l1, l2 = len(seq1), len(seq2)
dp = [[0] * (l2 + 1) for _ in range(l1 + 1)]
for i in range(1, l1+1):
for j in range(1, l2+1):
if seq1[i-1] == seq2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
print(dp[l1][l2])< 풀이 과정 >
주어진 두 문자열이 대문자로 구성되어 있고, 공백 제거 처리를 미리 해준다. (확인해보면 len결과가 주어진 문자열 + 1로 출력되는 것을 알 수 있다.)
이어서, 가로는 두번째 문자열 길이, 세로는 첫번째 문자열 길이로 2차원 dp 배열을 만들어준다.
두 문자열 길이만큼 반복문을 사용하여 만일 두 문자열의 문자가 일치하면, 이전 dp 배열의 인덱스 위치 + 1을 하여 부분 수열 개수를 늘려주고, 아닌 경우 이전 행, 열 과 비교해 더 큰 값을 저장한다.
최종적으로, dp 배열의 제일 마지막 부분을 출력해주면 주어진 두 문자 수열의 LCS 길이이다.
