
✅ 문제 풀이 - BOJ (Dynamic Programming)
🎈 11052 카드 구매하기
구매하려는 카드 개수 N이 주어지고, 둘째 줄에는 카드 팩 종류의 금액이 적혀져 주어진다.
ex) 카드 팩 종류의 금액 : 1 5 6 7 >> 카드 1개가 담긴 카드 팩 1원, 2개가 담긴 팩 : 5원 ... 이때, 지불해야 하는 금액의 최대값을 출력하는 문제
import sys
input = sys.stdin.readline
n = int(input())
pay = [0] + list(map(int, input().split()))
dp = [0]*(n+1)
for i in range(1, n+1):
for j in range(1, i+1):
dp[i] = max(dp[i], dp[i-j] + pay[j])
print(dp[n])< 풀이 과정 >
주어진 카드 팩 개수별 금액 정보를 dp와의 인덱스를 맞춰주기 편하도록 앞에 [0]을 더해 처리해준다.
그 이후, 다음과 같은 방식으로 dp내 금액을 집어넣는다.
n = 1 : dp[1] = pay[1]
n = 2 : dp[2] = max(pay[2], dp[1] + pay[1])
n = 3 : dp[3] = max(pay[3], dp[2] + pay[1], dp[1] + pay[2]) 로 비교가 가능하다.
이를 구현하고자 for문으로 (1,n+1), (1,i+1)로 탐색을 진행해 dp의 카드 개수 별 최대 금액을 출력하도록 한다.
🎈 2293 동전 1
n가지 종류의 동전이 있고 각 동전은 가치가 다르며 가치의 합을 k원으로 만들고 싶을 때 만들 수 있는 경우의 수를 구하는 문제
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
coin = [int(input()) for _ in range(n)]
dp = [0]*(k+1)
dp[0] = 1
for i in coin:
for j in range(i, k+1):
dp[j] += dp[j-i]
print(dp[k])< 풀이 과정 >
n, k는 정수로 coin은 리스트 형태로 변수를 저장하고, dp를 k원을 만드는 경우의 수를 의미하는 리스트로 생성한다.
dp[0]은 동전 1개를 사용하는 경우를 의미하므로 1로 저장한 후, coin을 이용하여 dp를 채워야 하므로 for문으로 coin을 돌고, for문으로 i원 ~ k원까지 만드는 경우의 수는 결국 dp[j] + dp[j-i]와 같다.
dp[j] : j원을 만드는 경우의 수 (j : i원 ~ k원의 범위)
dp[j-i] : j-i원을 만든 후 i원을 더해 j원을 만드는 경우의 수를 의미
🎈 9656 돌 게임 2
n개의 돌이 주어지고 상근이와 창영이가 턴을 번갈아가며 돌을 1개 또는 3개씩 가져갈 수 있을 때 이기는 사람을 구하는 문제 (턴은 상근이가 먼저 시작하며 상근이가 이기면 SK, 창영이가 이기면 CY출력)
import sys
input = sys.stdin.readline
n = int(input())
if n % 2 == 1:
print('CY')
else:
print('SK')< 풀이 과정 >
n을 5까지 대입하여 구현해보면 번갈아가며 돌이 홀수일때는 창영이가, 짝수일땐 상근이가 이기는 것을 알 수 있다.
🎈 11057 오르막 수
수의 길이 n이 주어질 때 오르막 수의 개수를 10007로 나눈 나머지를 구하는 문제
오르막 수란, 주어진 자리수가 오름차순으로 구성된 수를 의미한다. ex) 1234, 1235
오르막 수는 0으로 시작할 수 있다.
import sys
input = sys.stdin.readline
n = int(input())
dp = [1] * 10
for i in range(n-1):
for j in range(1, 10):
dp[j] += dp[j-1]
print(sum(dp) % 10007)< 풀이 과정 >
dp를 각 숫자의 빈도수로 나타내고 n이 1인 경우는 각 자리수가 한 번씩 나타난 것이므로 dp의 합을 10으로 나타낸다. 이후 9로 끝나는 오르막 수를 살펴보면 다음과 같다.
n = 1 : 9로 1개
n = 2 : 09,19 ... 99 까지 10개
n = 3 : 009 019 ~ 999까지 55개
즉, n이 커질수록 각 자리 수는 이전 row의 해당 숫자까지의 합으로 이루어 짐을 알 수 있다.
따라서 dp[j] += dp[j-1]로 반복 계산해준다.
🎈 11051 이항 계수 2
자연수 n과 k가 주어질 때 nCk를 구하는 문제
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
dp = [[1]*(k+1) for _ in range(n+1)]
for i in range(1, k+1):
for j in range(i+1, n+1):
dp[j][i] = dp[j-1][i] + dp[j-1][i-1]
print(dp[n][k] % 10007)< 풀이 과정 >
n, k를 정수로 입력받아 nXk의 1로 채워진 2차원 그래프를 dp로 생성한 후 2중 for문으로 값을 갱신한다. 이때 갱신 기준은, nCk = n-1Ck + n-1Ck-1 의 수학적 공식을 이용하여 값을 더해준다. 첫번째 for문의 경우 i는 k를 의미하고, 두번째 for문의 경우 n을 의미한다.
🎈 11055 가장 큰 증가하느 부분 수열
수열 A가 주어졌을 때 값이 증가하는 부분 수열 중 합이 가장 큰 것을 구하는 문제
n = int(input())
seq = list(map(int, input().split()))
dp = [0]*n
dp[0] = seq[0]
for i in range(1, n):
for j in range(i):
if seq[j] < seq[i]:
dp[i] = max(dp[i], dp[j] + seq[i])
else:
dp[i] = max(dp[i], seq[i])
print(max(dp))< 풀이 과정 >
n과 seq를 입력받고 길이가 n인 리스트 dp를 만들어주고 dp초기값을 seq 초기값과 일치시켜준다.
그 이후 dp[n]까지 탐색을 진행하는데, j로 range(i)를 돌며 seq[i] 현재 위치한 순열에 값이 이전 값들 보다 크다면, 값이 증가한 것을 의미하므로 dp[i]에 dp[i]와 dp[j] + seq[i]를 비교하여 큰 값을 넣어준다.
이때 dp[j]는 순열에서 j번째 인덱스의 최대값을 의미하고 seq[i]는 값이 증가함으로써 추가되는 값을 의미한다.
반대의 경우에는 dp[i]와 현재 순열의 값을 비교하여 큰 값을 출력한다.
🎈 1699 제곱수의 합
자연수 n을 입력받아 제곱수의 합으로 해당 자연수 n을 나타낼 때 최소 개수를 구하는 문제.
ex) n = 7 > 2^2 + 1^2 + 1^2 + 1^2으로 4개
import sys
input = sys.stdin.readline
n = int(input())
dp = [0] * (n+1)
for i in range(1, n+1):
dp[i] = i
for j in range(1, i):
if j**2 > i:
break
if dp[i] > dp[i-j**2] + 1:
dp[i] = dp[i-j**2] + 1
print(dp[n])< 풀이 과정 >
-
첫번째 for문으로 (1,n+1)범위를 지정해 dp[i] 값을 미리 선정하고 두번째 for문으로 (1, i)범위를 지정해 i이전의 값들로 i번째 dp 값을 계산할 수 있도록 설정하였다.
-
중요한 것은, n이 제곱수일 때 dp 결과 값은 1이 나와야 한다는 점이다. 그리고 다음과 같은 경우를 살펴보면 dp[i] > dp[i-j**2] + 1로 조건을 걸어준 이유를 알 수 있다.
n = 9인 경우, 앞선 조건을 통해 dp[9] = dp[9-1]+1, dp[9-4]+1, dp[9-9]+1로 결과가 나오는데, 숫자 9는 3^2이므로 결과는 1이 나와야 한다.
그러나 for문 특성 상 dp[8]+1부터 계산되는데, dp[i] = i를 미리 설정해줌으로써 더 작은 값을 찾아 갱신하는 구조로 탐색을 진행하게 된다.
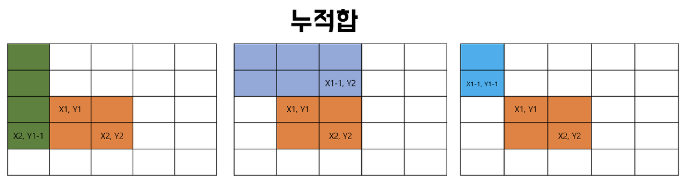
🎈 11660 구간 합 구하기 5
표의 크기 n과 합을 구해야 하는 횟수 m이 주어지고 m줄 동안 x1,y1,x2,y2가 주어질때 표에서 해당 범위의 값들의 합을 구하는 문제
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
graph = [list(map(int, input().split())) for _ in range(n)]
dp = [[0]*(n+1) for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, n+1):
dp[i][j] = dp[i-1][j] + dp[i][j-1] + graph[i-1][j-1] - dp[i-1][j-1]
for _ in range(m):
x1, y1, x2, y2 = map(int, input().split())
print(dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1])< 풀이 과정 >
누적합을 이용하여 구현한 풀이.
dp를 이용하여 누적합을 구하는데, i,j위치의 값은 다음과 같다.
dp[i][j] = dp[i-1][j] + dp[i][j-1] + graph[i-1][j-1] - dp[i-1][j-1]
그리고, x1,y1,x2,y2를 입력받아 해당 범위를 구하려면 다음과 같다.
dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]
그림으로 살펴보면 다음과 같다.
🎈 11722 가장 긴 감소하는 부분 수열
수열 A가 주어지고, 가장 긴 감소하는 부분 수열을 구하는 문제
import sys
input = sys.stdin.readline
n = int(input())
seq = list(map(int, input().split()))
dp = [1] * n
for i in range(1, n):
for j in range(i):
if seq[i] < seq[j]:
dp[i] = max(dp[i], dp[j]+1)
print(max(dp))< 풀이 과정 >
dp를 n길이의 1로 가득찬 리스트로 생성한다.
첫번째 for문 dp별 인덱스를 부여하고, j는 range(i)로 0~i번째 인덱스를 부여한다.
2중 for문을 돌며 seq 리스트 내 i<j일때 값이 감소하는 조건을 유지한 채, dp[i]를 dp[j]+1과 비교해 더 큰 값을 가지도록 부여해준다.
🎈 2294 동전 2
정수 n, k를 입력받고 각 n개의 동전들의 가치가 주어지고 이 가치들의 조합으로 k원의 가치를 만들고자 할 때 사용한 동전의 최소 개수를 출력하는 문제. 불가능한 경우 -1을 출력한다.
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
coin = [int(input()) for _ in range(n)]
dp = [10001]*(k+1)
dp[0] = 0
for i in coin:
for j in range(i, k+1):
if dp[j] > 0:
dp[j] = min(dp[j], dp[j-i] + 1)
if dp[k] == 10001:
print(-1)
else:
print(dp[k])< 풀이 과정 >
dp[n]은 동전들로 n원을 만들때 최소가 되는 동전의 개수이고
for문으로 coin 중 동전을 고르고, j로 i~k 범위 내 인덱스를 지정해 dp[j-i] 중 개수가 가장 적은 경우를 택하고 1개의 동전만 더해 최소 동전개수를 고르게 만든다.
이후 k원을 만드는게 불가능한 경우 -1을, 아닌 경우 dp[k]를 출력하도록 한다.
✅ 문제 풀이 - 프로그래머스
🎈 호텔 대실
book_time으로 대실 시작 시간, 대실 종료 시간 형태로 입력을 받고 한 번 사용한 객실은 퇴실 후 10분 간 청소가 필요하다. 최종적으로 하루 동안 사용되는 객실 수를 출력하는 문제
def solution(book_time):
dic = {}
book_time.sort(key = lambda x: x[0])
for book in book_time:
start = int(book[0].split(':')[0]) * 60 + int(book[0].split(':')[1])
end = int(book[1].split(':')[0]) * 60 + int(book[1].split(':')[1])
for time in range(start, end+10):
if dic.get(time) == None:
dic[time] = 1
else:
dic[time] += 1
answer = max(dic.values())
return answer< 풀이 과정 >
주어진 예약정보를 우선 입실 시간을 기준으로 정렬해주어 방의 정보를 표시한다.
이후, for문으로 입실시간, 퇴실시간을 '분'기준으로 바꿔주고 범위를 지정해 dic에 분 당 개수를 추가하도록 만들어준다.
예를 들어 10:20 이 입실이고, 퇴실이 12:30 인 경우, 분으로 환산하면 620 ~ 750이고 퇴실 이후 10분간 청소시간을 더해 범위를 620 ~ 760으로 산정한다. 범위를 산정하여 모든 예약정보에 적용하면 동일 시간에 대해 '분'을 key로 가진 딕셔너리에 + 1씩 해주어서 값의 max값을 뽑으면 필요한 객실 수가 나오게 된다.
