
✅ Regression
회귀모델의 목표는 N차원의 벡터 x들이 input으로 주어질 때 그에 해당하는 연속 target 변수 t 값을 예측하는 것. 이때 입력 변수 X에 대한 비선형 함수들의 집합을 선형적으로 결합할 수 있는데, 이를 기저함수라고 한다. 기저함수의 매개변수 wo는 bias라고 부른다.
기저함수 예시로는 다항식 기저함수, 가우시안 기저함수, 시그모이드 기저함수가 존재한다.
다항식 기저함수의 경우, 한 변수의 변화가 타 변수에도 영향을 준다는 점인데, 이를 해결하고자 각 영역에 대해 서로 다른 fitting을 진행한 함수가 바로 spline 함수이다.
선형회귀 모델의 가장 큰 목표는 에러함수 (오차)를 최소화하는 것이다. 이 에러함수를 최소화하는 것이 최대가능도의 해를 구하는 것과 같으므로(에러함수가 가우시안 노이즈를 가정하는 경우, 최대우도로부터 유도 가능하기에) 해당 관계를 살펴보면 다음과 같다.
ϵ : 가우시안 분포를 따르는 노이즈 확률변수로 0을 평균으로 β를 정밀도로 가짐. y(x,w) : 결정론적 함수 t= y(x,w)+ϵ p(t|x,w,β)=N(t|y(x,w),β−1) 이때 파라미터인 w를 찾는 것이 목표이며, 최대우도추정법을 사용한 로그 우도함수를 최대시키는 w는 결국, 주어진 선형회귀 모델에서의 에러함수를 최소화 시키는 것과 같다.
- 에러함수
- 로그 우도함수
- w의 최적값은 결국 아래와 같고,
- 위 식을 normal equations라고 부른다.
위 식을 행렬 Φ의 Moor-Penrose pseudo-Inverse 라고 하며, 역행렬 개념을 정사각이 아닌 행렬들에 대해 일반화한 것이다.
🎈 How to minimize error?
선형회귀를 포함해 다양한 회귀 모델에서 에러를 최소화하는 방법은 SGD 경사하강법이다.
학습횟수와, 학습률을 파라미터로 갖는 해당 기법은 확률적 경사하강법과 순차적 경사하강법으로 나뉜다.
- 확률적 SGD : 무작위성으로 하나의 확률변수에 대해서만 gradient를 계산하여 수렴이 불안정
- 순차적 SGD : 한번의 iteration마다 모든 데이터에 대해 Weight업데이트 후 해당 평균을 사용해 가중치 업데이트 진행.
- 최소 제곱 평균(LMS 알고리즘)
이후 overfitting을 방지하기 위해서 regularization을 진행한다.
- L2 규제(Ridge) : weight 제곱에 비례하는 크기의 패널티를 가해 모델 가중치 값을 작게 만듬. 따라서 L2규제를 통해 가중치를 0에 가깝게 유지하여 다중공선성 문제 완화 가능.
-> Loss: MSE + α∑Wi^2- L1 규제(Lasso) : weight들의 절댓값에 비례하는 크기의 패널티를 가해 가중치 중 일부를 0으로 만들어 변수 선택을 자동으로 수행함. 따라서 특정 특성들의 영향을 줄이거나 제거하는 효과 존재.
-> Loss: MSE + α∑|Wi|- ElasticNet: L2와 L1 규제를 함께 사용하는 선형회귀 모델. 두 규제를 혼합 사용하므로 특정 특성 영향을 줄이고, 가중치를 0에 가깝게 유지하여 다중공선성도 해결한다!
선형회귀를 한 문장으로 요약한다면 최종적으로 에러를 최소화하기 위해 변수 별 계수라고 볼 수 있는 가중치 W를 찾는 문제.
대부분 ML (회귀 모델)들은 최대우도추정법을 활용하기에 오버피팅이 발생할 확률이 상당히 높은데, 이는 베이지안 방식으로 해결할 수 있긴 하다. (사전정보로써 모델 파라미터의 분포를 이미 정의하기도 하고, 사전확률과 우도확률로 부터 사후확률을 추정할 수 있으므로)
- 베이지안 선형회귀 : 선형회귀 모델에 베이지안 추론을 적용하여 최소제곱법이 아닌 가중치 분포를 미리 확인하는 확률적인 방법을 이용해 가중치를 추론하기에 가중치에 대한 불확실성을 표현할 수 있다. 특히 제한적인 데이터, 노이즈가 많은 경우 유용하게 사용된다.
-> 상대적으로 양이 적은 데이터에도 적합하게 사용될 수 있으나 일반 선형회귀보다 더 많은 계산이 필요하다는 단점이 존재하고, 적절한 가능도 함수와 사전 분포를 사용해야하는 부분에 있어 learning curve가 상대적으로 높은 편이다.
-> 하지만, 적절히 잘 사용한다면 overfitting은 물론, 가중치의 평균과 분산을 추정할 수 있어 비즈니스 의사결정에도 적합하게 적용될 가능성이 높다.
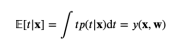
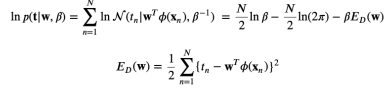
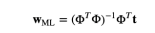
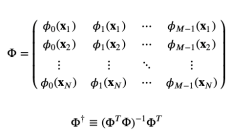
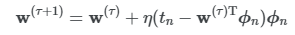

너무 좋은 글이네요. 공유해주셔서 감사합니다.