Graph Algorithms #3

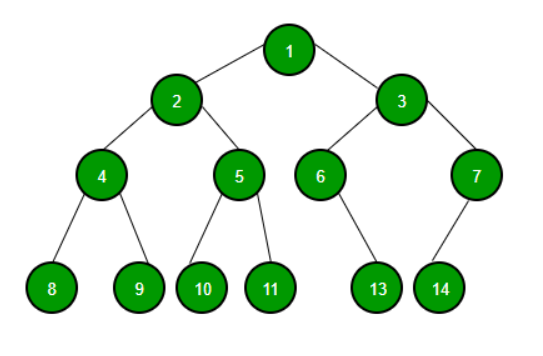
✅ Tree

• node, edge로 이루어진 자료 구조
• 부모-자식 관계로 구성되어 있음
• 사이클이 존재할 수 없고, 모든 노드는 자료형으로 표현이 가능
• node 수가 n개면 edge 수는 n-1, 루트에서 노드로 이동하는 경로는 유일하다.
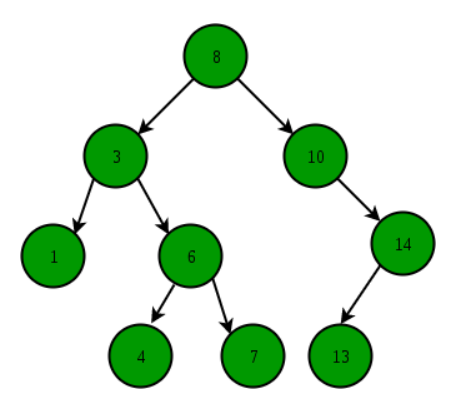
• 위 그림은 이진 트리로, degree가 모두 2이하로 재귀적으로 정의할 수 있다.
  이진트리란 ?
• 빈 트리 or 루트 + 왼쪽 서브트리 + 오른쪽 서브트리

📌 트리 순회 방식

1. 전위 순회(pre-order) : 각 루트를 순차적으로 먼저 방문 - DFS
   1 → 2 → 4 → 8 → 9 → 5 → 10 → 11 → 3 → 6 → 13 → 7 → 14
2. 중위 순회(in-order) : 왼쪽 하위트리 방문 이후 루트 방문 - BST
   8 → 4 → 9 → 2 → 10 → 5 → 11 → 1 → 6 → 13 → 3 →14 → 7
3. 후위 순회(post-order) : 왼쪽,오른쪽 서브트리를 순회, 그리고 나서 마지막으로 노드 x 를 방문
   8 → 9 → 4 → 10 → 11 → 5 → 2 → 13 → 6 → 14 → 7 → 3 → 1
4. 레벨 순회(level-order) : 루트 부터 계층 별로 방문 - BFS
   1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 → 11 → 13 → 14

✅ BST

이진탐색 + 연결리스트 형태로 효율적인 탐색 능력으로 자료 삽입/삭제 가능토록 하기 위함
이진탐색: 탐색 소요 시간복잡도 : O(logN), 삽입/삭제 X
연결리스트: 삽입/삭제 O(1), 탐색 O(N)

• 각 노드의 자식은 2개 이하여야 함

• 각 노드의 왼쪽 자식이 부모보다 작고 오른쪽은 부모보다 커야한다.

• 중복된 노드가 없어야 한다

• 균등트리 : O(logN), 편향 트리 : O(N)
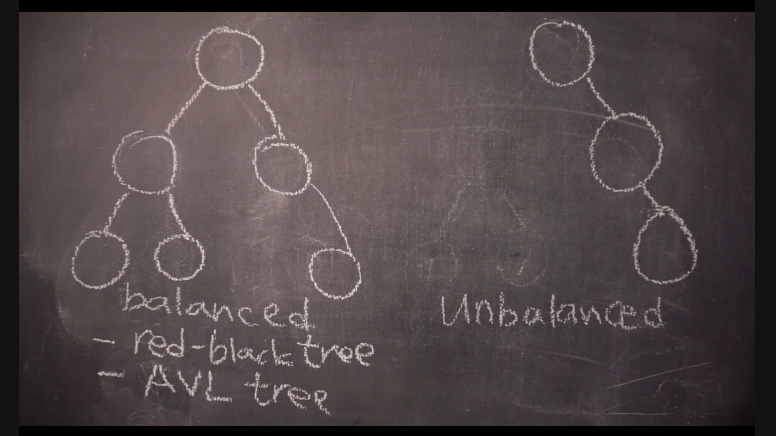
  그러나, 편향트리는 시간복잡도가 O(n)이므로 트리를 사용할 이유가 없기에 이를 개선한 것이 AVL Tree, RedBlack Tree이다.

• 삭제 3가지 case

1. 자식이 없는 leaf 노드 > 그냥 삭제
2. 자식이 1개인 노드 : 지워진 노드에 자식 부모노드로 올리기
3. 자식이 2개인 노드 : 오른쪽 자식 노드에서 가장 작은 값 or 왼쪽 자식 노드 중 가장 큰값 올리기

BST 종류
1. BT vs BST

2. Balanced vs Unbalanced

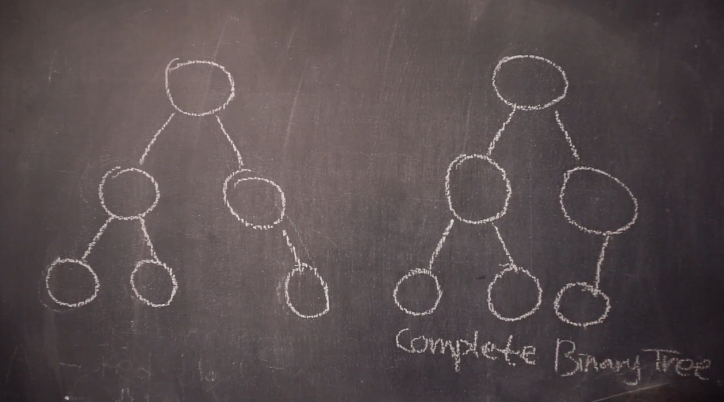
3. Complete BT (왼쪽 노드부터 채워진 형태를 의미)

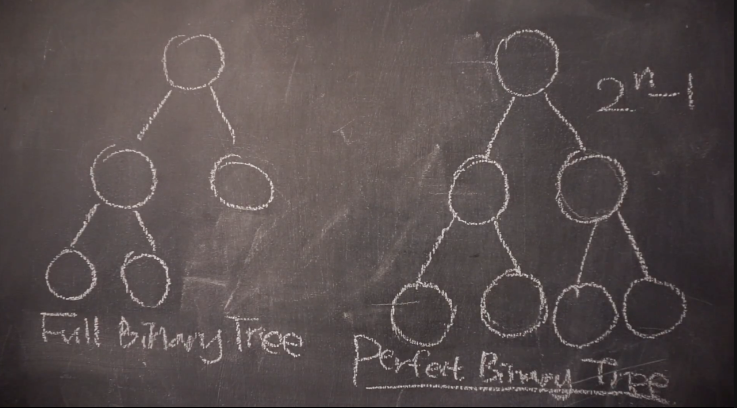
4. Full BT(자식노드가 2개 혹은 0개) vs Perfect BT(노드 수는 2^레벨수 - 1로 고정)

✅ Trie

• 문자열에서 검색을 빠르게 도와주는 자료구조
• BST 이용 시 정수형에서 O(logN), 문자열 적용 시 문자열 최대 길이 m인 경우 O(mlogN)이 되기에 트라이를 활용한다면 O(m)으로 탐색이 가능해진다.

✅ B-Tree

정리해놓은 기존 링크 참고
링크텍스트