Sorting Algorithms #1

코딩 테스트는 물론, 기본적인 정렬 알고리즘들에 대해 학습하고자 한다.

✅ Bubble sort

• selection sort와 유사한 알고리즘, 서로 인접한 두 원소의 대소를 비교해 자리 교환하며 정렬
• 시간복잡도의 경우 O(n^2), 주어진 array내 교환이므로 공간복잡도는 O(n)
• 구현이 간단하며 stable한 정렬
• 배열의 길이가 깊어지면 비효율적
• 시간복잡도가 상당히 비효율적, 정렬되어 있지 않은 배열의 경우 교환 연산 비약적 증가

bubble sort 동작과정은 다음과 같다
1. 1회전에 전체를 순환하며 인접한 두 원소 비교 및 교환 진행
2. 1번 수행 시 가장 큰 원소 맨 뒤로 정렬되고 나머지 데이터로 비교 및 교환 진행
3. 1,2 번 반복하여 교환 안 일어나면 중단

코드로 기초적인 bubble sort구현방식을 알아보면 다음과 같다.

def bubble_sort(array):
	# 뒤부터 탐색시작
    for i in range(len(array)-1, 0, -1):
    	# 최적화를 위해 진행
        check = False
    	for j in range(i):
        	if array[j] > array[j+1]:
            	array[j], array[j+1] = array[j+1], array[j]
				check = True
        # 교환 일어나지 않으면 정렬 완료
		if not check:
        	break
    return array

✅ Selection sort

• 해당 순서에 원소 넣을 위치는 이미 정해져있고, 어떤 원소를 넣을 지를 선택하는 알고리즘
• O(n^2)의 시간복잡도와 O(n)의 공간복잡도를 가짐
• 많은 교환 필요한 배열에 비교적 효율적
• 배열의 길이가 깊어지면 비효율적
• unstable한 정렬 형태.
• bubble 정렬과 유사하지만 조금 더 빠른 편(실제 교한 횟수 적기에)

Selection sort 동작과정은 다음과 같다
1. 주어진 배열 중 최솟값 찾기
2. 그 값을 맨 앞에 위치한 값과 교체
3. 1,2번 반복 진행

코드로 기초적인 selection sort 구현방식을 알아보면 다음과 같다.

def selection_sort(array):
	# 뒤부터 탐색
    for i in range(len(array)-1):
        # 최솟값 인덱스 저장
        min_idx = i
        # 지정한 인덱스 ~ 이후 탐색
        for j in range(i+1, len(array)):
        	# 최솟값이 더 크면 변경
            if array[j] < array[min_idx]:
                min_idx = j
        array[i], array[min_idx] = array[min_idx], array[i]
    return array

✅ Insertion sort

• 2번째 원소부터 시작해 그 앞의 원소들과 비교해 삽입 위치 지정 후 원소를 뒤로 옮기고 지정된 자리에 자료 삽입
  평균 및 최악의 경우 O(n^2)의 시간복잡도, O(n)의 공간복잡도
  메모리 공간을 필요로 하지 않는 inplace sorting, stable sort이며 상대적으로 bubble, selection에 비해 빠르다.
• 배열의 길이가 깊어지면 비효율적

Insertion sort 동작과정은 다음과 같다
1. 정렬은 두번째 위치의 idx값을 temp에 저장
2. temp와 이전에 있는 원소들을 비교하며 삽입
3. 1,2번 반복

코드로 기초적인 Insertion sort 구현방식을 알아보면 다음과 같다.

def Insertion_sort(array):
    for end in range(1, len(array)):
        # 초기값 지정
        i = end
        # 초기값이 다음 값보다 크면 변경
        while i > 0 and array[i - 1] > array[i]:
            array[i - 1], array[i] = array[i], array[i - 1]
            i -= 1
    return array

✅ Quick sort

분할 정복 방법을 통해 주어진 배열 정렬

• 배열을 비균등하게 분할하고 임의 접근하므로 unstable 정렬
• 파이썬에 내장된 sort()는 퀵정렬 기본 지원
• O(nlogn)의 시간복잡도, 최악의 경우 O(n^2), 공간복잡도는 O(logn)

Quick sort 동작과정은 다음과 같다
1. 배열 가운데 원소 하나를 골라 pivot으로 지정
2. 피벗 값 기준으로 큰 값, 작은 값 두 배열로 나눈다.
3. 재귀적으로 반복

코드로 기초적인 Quick sort 구현방식을 알아보면 다음과 같다.

def quick_sort(array):
    # 재귀함수 만들기
    def sort(low, high):
        if high <= low:
            return
        mid = partition(low, high)
        sort(low, mid - 1)
        sort(mid, high)

    def partition(low, high):
        # 가운데 값 피벗 지정
        pivot = array[(low + high) // 2]
        # 인덱스 교차하기 전까지 진행
        while low <= high:
            # 올바르게 정렬 시 + 1
            while array[low] < pivot:
                low += 1
            # 큰 값들 정렬
            while array[high] > pivot:
                high -= 1
            # 인덱스 교차 이전 값 변경
            if low <= high:
                array[low], array[high] = array[high], array[low]
                low, high = low + 1, high - 1
        return low
    return array

✅ Merge sort

• 분할 정복 방법으로 구현
• stable 정렬에 속하며 O(nlogn)의 균일한 시간복잡도, O(n)의 공간복잡도를 가진다.
• 연결리스트에 정렬 필요한 경우 순차접근하는 병합정렬 사용 시 효율적이다.
• 분할하는 방식은 퀵정렬과 유사하지만, 피벗이 아닌 중앙값으로 이를 분리하고 분할한 요소들을 다시 병합하며 정렬하는 방식

Merge sort 동작과정은 다음과 같다
1. 더 이상 분할할 수 없을 때까지 요소들을 분할
2. 2개씩 병합하며 작은 숫자가 앞에 오도록 위치시킴
3. 배열들을 순서대로 합치며 정렬

코드로 기초적인 Merge sort 구현방식을 알아보면 다음과 같다.

def Merge_sort(array):
    # 더 이상 분할 x
    if len(array) < 2:
        return array
    # 가운데 값 지정
    mid = len(array) // 2
    # mid 기준 배열 분할
    low_arr = Merge_sort(array[:mid])
    high_arr = Merge_sort(array[mid:])
	# 병합 배열 생성
    merged_arr = []
    l = h = 0
    # 주어진 범위 내 더 작은 값 앞에 오도록 배치
    while l < len(low_arr) and h < len(high_arr):
        if low_arr[l] < high_arr[h]:
            merged_arr.append(low_arr[l])
            l += 1
        else:
            merged_arr.append(high_arr[h])
            h += 1
    merged_arr += low_arr[l:]
    merged_arr += high_arr[h:]
    return merged_arr

✅ Heap sort

• 완전 이진 트리를 기본으로 하는 힙 자료구조 기반 정렬 방식
• unstable 정렬에 속하며 최대힙을 이용한 내림차순정렬, 최소힙을 이용한 오름차순 정렬 존재
• 최대, 최소 값 구하는데 유용하고 최대 k만큼 떨어진 원소 정렬 시 유용하다.
• O(nlogn)의 시간복잡도를 가진다.

Heap sort의 동작과정은 다음과 같다
1. 최대 힙을 구성
2. 현재 힙 루트에 가장 큰 값이 존재하는 경우 루트의 값을 마지막 요소와 바꾼 후 heap_size - 1
3. heap_size > 1인 경우 위 과정 반복

코드로 기초적인 Heap sort 구현방식을 알아보면 다음과 같다.

def Heap_sort(array):
    n = len(array)
    # heap 구성
    for i in range(n):
        c = i
        while c != 0:
            r = (c-1)//2
            if array[r] < array[c]:
                array[r], array[c] = array[c], array[r]
            c = r
    # 크기를 줄여가면서 heap 구성
    for j in range(n-1, -1, -1):
        array[0] , array[j] = array[j], array[0]
        r = 0
        c = 1
        while c<j:
            c = 2*r +1
            # 자식 중 더 큰 값 찾기
            if (c<j-1) and (array[c] < array[c+1]):
                c += 1
            # 루트보다 자식이 크다면 교환
            if (c<j) and (array[r] < array[c]):
                array[r], array[c] = array[c], array[r]
            r=c
    return array

✅ Binary Search

• 처음부터 끝까지 탐색하는 것보다 훨씬 효율적 (시간복잡도: O(n))
• 과정은 생략하고, 시작인덱스와 끝인덱스로 값을 가운데로 줄여가며 탐색하는 방법
• 이미 정렬된 리스트로 탐색 실행

이진 탐색 알고리즘을 구현하면 다음과 같다.

# sorted_list : 이미 정렬된 배열
# num : 찾고자 하는 값
def binary_search(sorted_list, num):
    left = 0
    right = len(sorted_list) - 1
    # 인덱스끼리 교차하기 전까지만
    while left <= right:
        # 가운데 인덱스 지정
        mid = (left+right) // 2
        # 찾는 값이 배열 가운데 값 보다 작으면, 끝 인덱스 변경
        if num < sorted_list[mid]:
            right = mid - 1
        # 반대의 경우 시작인덱스 변경
        elif sorted_list[mid] < num:
            left = mid + 1
        # 번호를 찾은 경우 mid 값 리턴
        else:
            return mid
    # 주어진 배열 내 찾고자하는 num 존재 X
    return -1

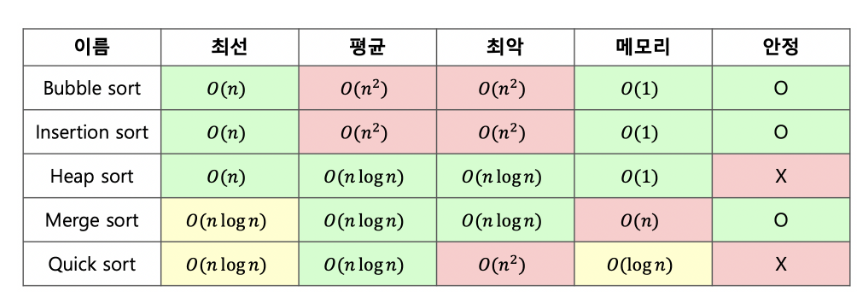
🎇 정리 및 참고 자료

잘 알려진 정렬 기법에 대해 정리한 표이다.
+) Tim Sort
위 링크는 파이썬에서 사용되는 sorted 등 정렬 알고리즘에 적용되는 동작방식에 대해 깔끔히 작성된 글로 참고하면 좋을 듯 하다.