그래프란?
- 정점(vertex)와 정점을 연결하는 간선(edge)로 이루어진 자료구조
- 단방향 / 양방향 그래프로 나뉨
- 간선에 가중치가 존재하기도 함
- degree: 정점에 연결된 간선 수
- indegree: 해당 정점으로 들어오는 간선 수
- outdegree: 해당 정점에서 나가는 간선 수
인접 행렬 (Adjacency Matrix)
- 두 정점간의 관계를 N*N 행렬(2차원 배열)로 나타낸 것
- 만약 1, 2 정점이 연결되었다면 Adj[1][2]=1, Adj[2][1]=1이 되는 것
- 특정 노드를 조회하는 것은 O(1), 모든 정점 확인하면 O(n)
- 정점들 사이의 연결 관계를 확인해야 하는 경우 사용
인접 리스트 (Ajdency List)
- 각 정점에 연결된 정점들을 리스트(1차원 배열)에 보관
- 연결된 정점들을 탐색해야하는 경우
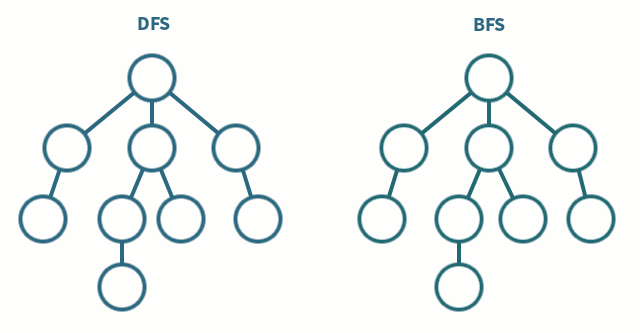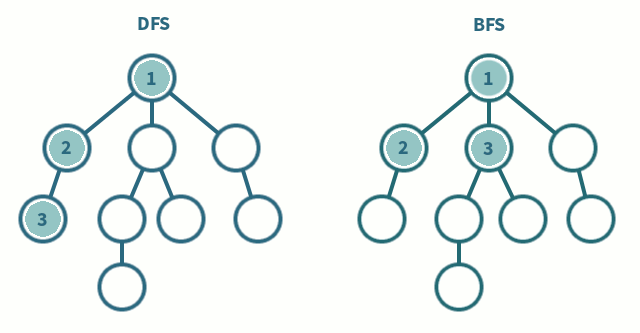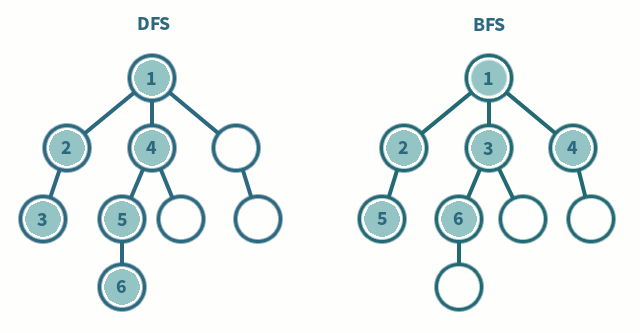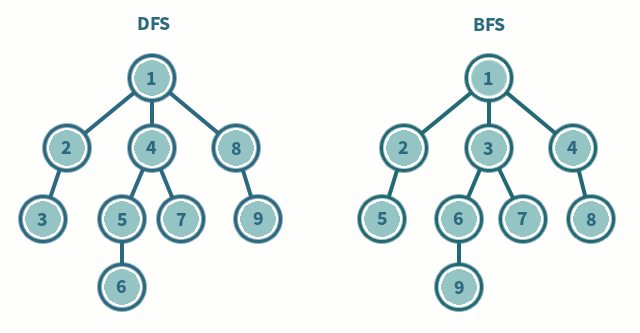
DFS (깊이 우선 탐색)
- 최대한 깊게 탐색하고 빠져 나옴
- 스택 or 재귀 함수 사용
- 가중치가 주어지거나, 특정 경로를 찾아야할 때 사용
DFS에서 스택을 사용하는 이유?
스택은 Last in First Out이라는 성격을 띈 자료구조라서 가장 최근에 탐색한 노드의 자식을 탐색해야하는 DFS에 적절한 자료구조이다.
BFS (너비 우선 탐색)
- 넓게 자신의 자식들부터 탐색
- 큐 사용
- 최단거리를 찾을 때 사용 ex) 미로 찾기
BFS에서 큐를 사용하는 이유?
큐는 First in First Out이라는 성격을 띄고 있으므로 가장 최근에 탐색한 노드들이 먼저 pop되기 때문에 넓게 자신의 자식들을 먼저 탐색하는 BFS에 적절한 자료구조이다.
다양한 그래프 알고리즘
- 정점들 사이 최단거리 → 최단 경로 알고리즘 (다익스트라, 플로이드-와샬, 벨만 포드 등)
- 사이클이 없는 그래프 → 트리
- 가중치의 합이 작은 트리를 만들어야 할 때 → 최소 비용 신장 트리
- 선후 관계가 주어진 그래프 → 위상정렬
- 정점 사이의 관계를 집합으로 나눌 때 → 유니온 파인드
DFS 예제
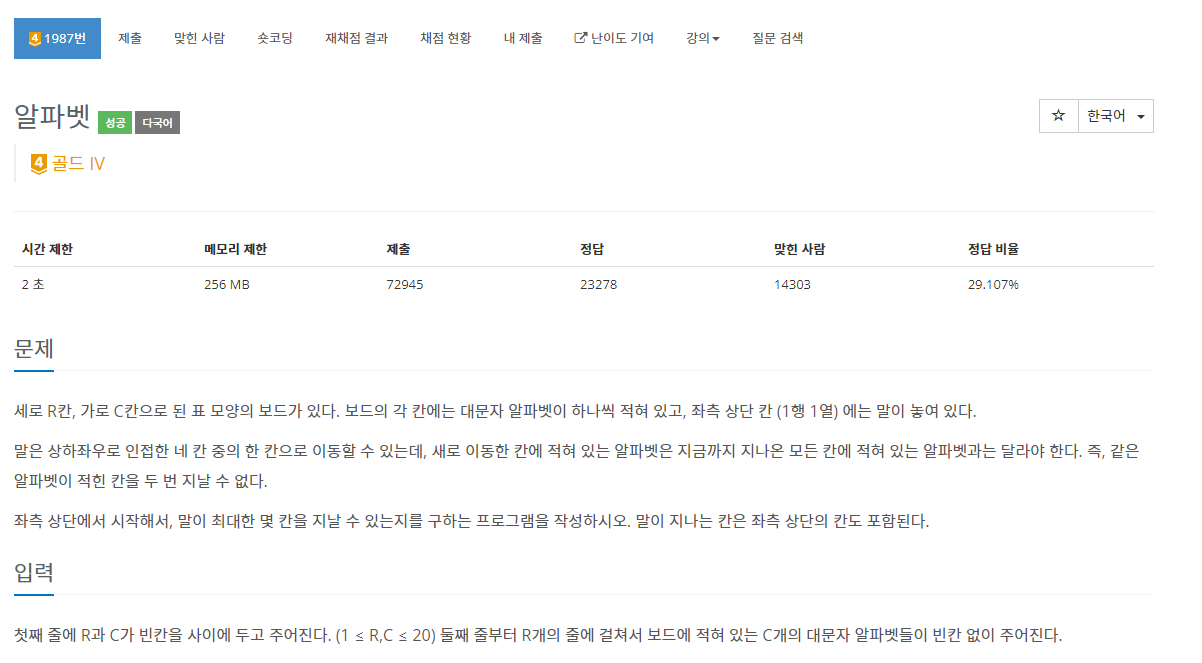
접근 💡
- 좌측 상단에서 시작해서 이동하는 경로를 찾는 문제이므로 DFS를 사용해야 함
- (r,c)에서 상, 하, 좌, 우로 이동할 수 있고, 방문하지 않은 노드라면 이동하고 탐색 재개
- 알파벳이 다 달라야 하므로 지나간 곳의 알파벳을 저장하는 배열도 필요함
코드 💻
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int R, C;
vector<vector<char>> board;
vector<char> alphabet;
vector <vector<bool>> visited;
int dx[4] = { 0, 0, -1, 1 };
int dy[4] = { -1, 1, 0, 0 };
int answer = 1;
void dfs(int x, int y, int cnt) {
for (int i = 0; i < 4; i++) {
int nextX = x + dx[i];
int nextY = y + dy[i];
// 다음 보드로 이동할 수 있는지
if (nextX >= 0 && nextX < R && nextY >= 0 && nextY < C) {
//이미 방문한 알파벳인지
auto isfound = find(alphabet.begin(), alphabet.end(), board[nextX][nextY]);
if (!visited[nextX][nextY] && isfound == alphabet.end()) {
visited[nextX][nextY] = true;
alphabet.push_back(board[nextX][nextY]);
dfs(nextX, nextY, cnt+1);
visited[nextX][nextY] = false;
alphabet.pop_back();
}
}
}
if (cnt > answer) answer = cnt;
}
int main() {
cin >> R >> C;
board.resize(R, vector<char>(C));
visited.assign(R, vector<bool>(C, false));
for (int i = 0; i < R; i++) {
for (int j = 0; j < C; j++) {
cin >> board[i][j];
}
}
visited[0][0] = true;
alphabet.push_back(board[0][0]);
dfs(0, 0, 1);
cout << answer;
}BFS 예제
접근 💡
- A가 B, C에게 루머를 유포한다면 B, C가 다음 사람들에게 유포하게 됨
- 동시에 루머가 퍼지므로 BFS 이용
코드 💻
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
vector<int> bfs(vector<vector<int>>& v, vector<int>& rumor, int N, int M) {
vector<int> answer(N+1, -1);
vector<int> rest(N + 1, 0);
queue<int> q;
//최초 유포자
for (int i = 0; i < M; i++) {
answer[rumor[i]] = 0;
q.push(rumor[i]);
}
//i번째 사람의 주위 사람들의 절반 수
for (int i = 1; i <= N; i++) {
rest[i] = (v[i].size() + 1) / 2;
}
while (!q.empty()) {
int cur = q.front();
int t = answer[cur];
q.pop();
for (int i = 0; i < v[cur].size(); i++) {
int next = v[cur][i];
//이미 루머를 믿고 있는 경우
if (answer[next] > -1) continue;
//next는 루머를 믿고있는 cur의 지인이므로 믿어야 하는 사람 한명 감소
rest[next]--;
//주변 절반 이상이 믿고 있다면 큐에 넣음
if (!rest[next]) {
answer[next] = t + 1;
q.push(next);
}
}
}
return answer;
}
int main() {
int N, M;
cin >> N;
vector<vector<int>>v(N + 1);
for (int i = 1; i <= N; i++) {
while (true) {
int rel;
cin >> rel;
if (rel == 0) break;
v[i].push_back(rel);
}
}
cin >> M;
//rumor은 믿은 시간을 담는 배열
vector<int> rumor(M, 0);
for (int i = 0; i < M; i++) {
cin >> rumor[i];
}
vector<int> answer = bfs(v, rumor, N, M);
for (int i = 1; i <= N; i++) {
cout << answer[i] << " ";
}
}