[알고리즘] 그리디 알고리즘

이제는 미룰 수 없다 나의 알고리즘 정리..

그리디 알고리즘이란?

• 현재 상황의 최선의 선택이 전체의 최선의 선택이 됨
• 모든 순간 답이 되는 것은 아님 → 조건을 만족해야 그리디 알고리즘을 적용할 수 있음

그리디 알고리즘 조건

1. 탐욕 선택 조건
   • 이 선택으로 인해 최적해를 반드시 도출할 수 있어야 함
2. 최적 부분 구조
   • 부분 문제의 최적 결과가 전체에도 적용될 수 있어야 함
   • 대부분 문제에서 이 조건은 당연하기 때문에 별도로 증명할 필요 없음

예제

백준 1931 회의실 배정

대표적인 그리디 알고리즘 문제이다.
만약 이 문제를 그냥 푼다고 한다면 N이 10의 5승이므로 무조건 시간 초과가 날 것이다.

접근 💡

• 회의 시작 시간과 끝 시간이 주어짐
• 회의가 겹치지 않게 사용하는 회의실 최대 개수
• 그렇다면 회의를 일찍 시작하는 순서대로 고른다면?

→ 반례❗

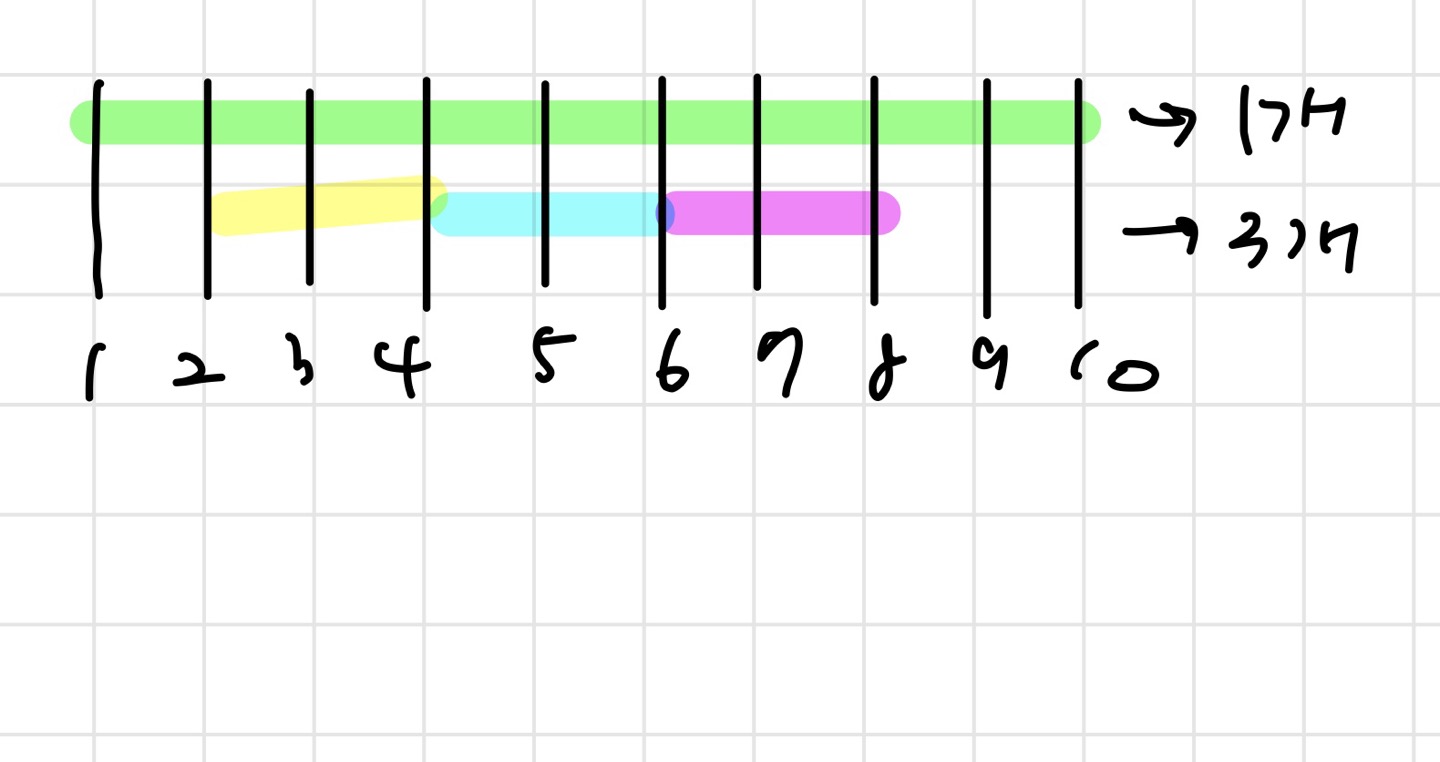
회의 시간이 (1, 10) (2, 4), (4, 6), (6, 8)로 주어졌을 때 1~10까지 예약할 수 있다고 할 때 (1, 10)을 선택하는 것보다 나머지 셋을 선택하는 것이 더 최적해이다.

• 회의가 끝나는 시간이 빠를 수록, 더 많은 회의를 배치 할 수 있다.
• 끝나는 시간이 같다면, 시작 시간이 빠를 수록 더 많은 회의를 배치할 수 있다.

이유

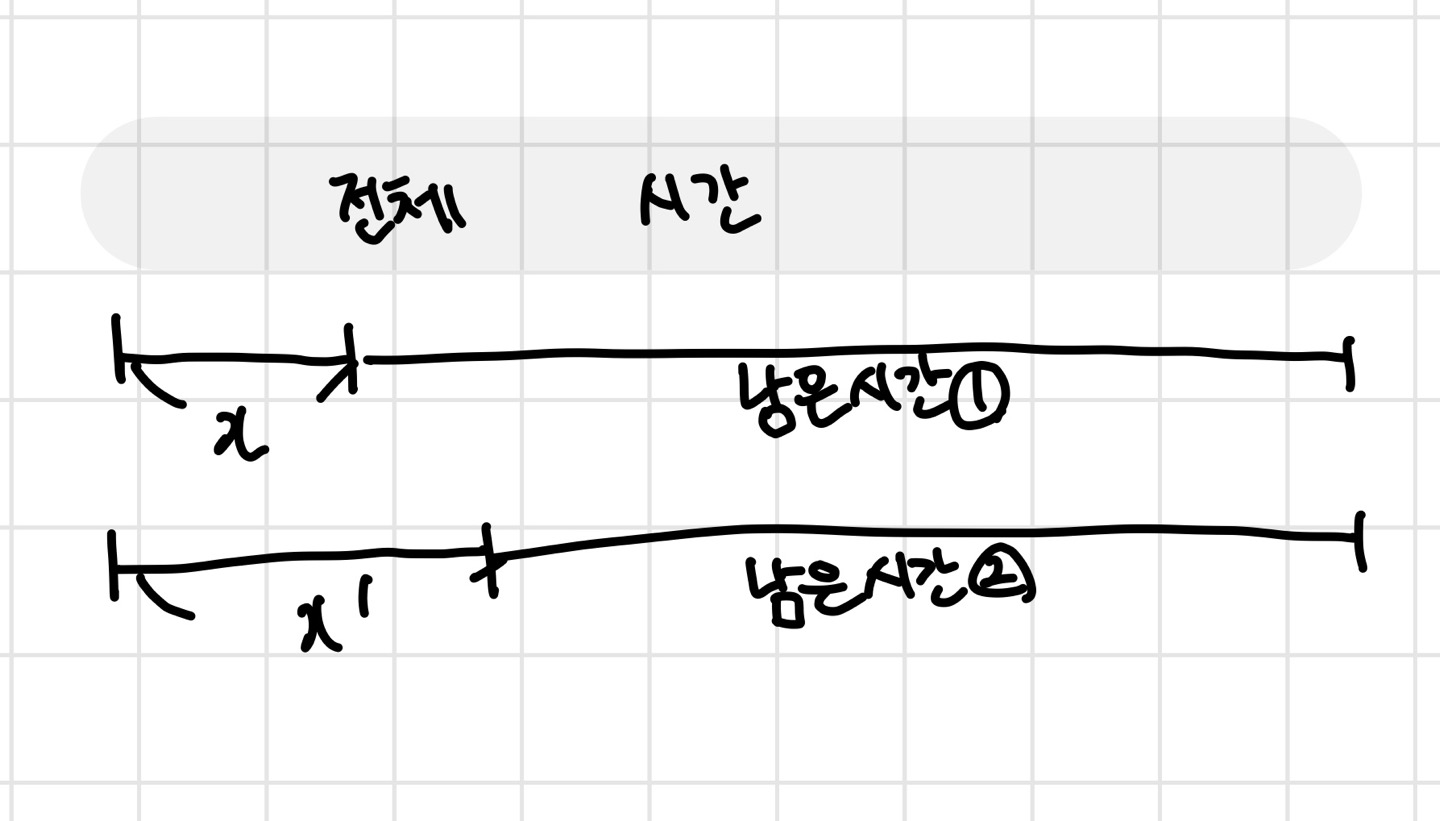
같은 전체 시간이 주어질 때, 남은시간1>남은시간2일 때 회의수가 후자가 더 많을 수가 없다. 따라서 순간 선택으로 최적해를 도출해낼 수 있다.

코드💻

//끝나는 시간이 빠른 순서로 정렬
bool comp(pair<int, int>a, pair<int, int> b) {
	if (a.second == b.second) {
		return a.first < b.first;
	}
	return a.second < b.second;
}

int main() {
	int n; //회의 수
	int start;
	int end;
	vector<pair<int, int>> meeting;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> start >> end;
		meeting.push_back(make_pair(start, end));
	}
	sort(meeting.begin(), meeting.end(), comp);
	int time = 0;
	int answer = 0;
	for (int i = 0; i < n; i++) {
		if (time <= meeting[i].first) {
			time = meeting[i].second;
			answer++;
		}
	}
	cout << answer;
}

그리디 문제들은 구현자체는 쉬운데 이 문제가 그리디인가를 추론하는 과정이 어려운 것 같다.