1. 문제 링크
https://www.acmicpc.net/problem/10423
2. 문제
요약
- 발전소를 만들 때 중요한 것은 발전소 건물과 도시로 전기를 공급해주는 케이블인데, 이미 발전소는 특정 도시에 건설되어 있고, 추가적으로 드는 비용은 케이블을 설치할 때 드는 비용이 전부입니다.
- 케이블을 설치할 때 드는 비용이 커서 이를 최소화해서 설치하여 모든 도시에 전기를 공급하려고 합니다.
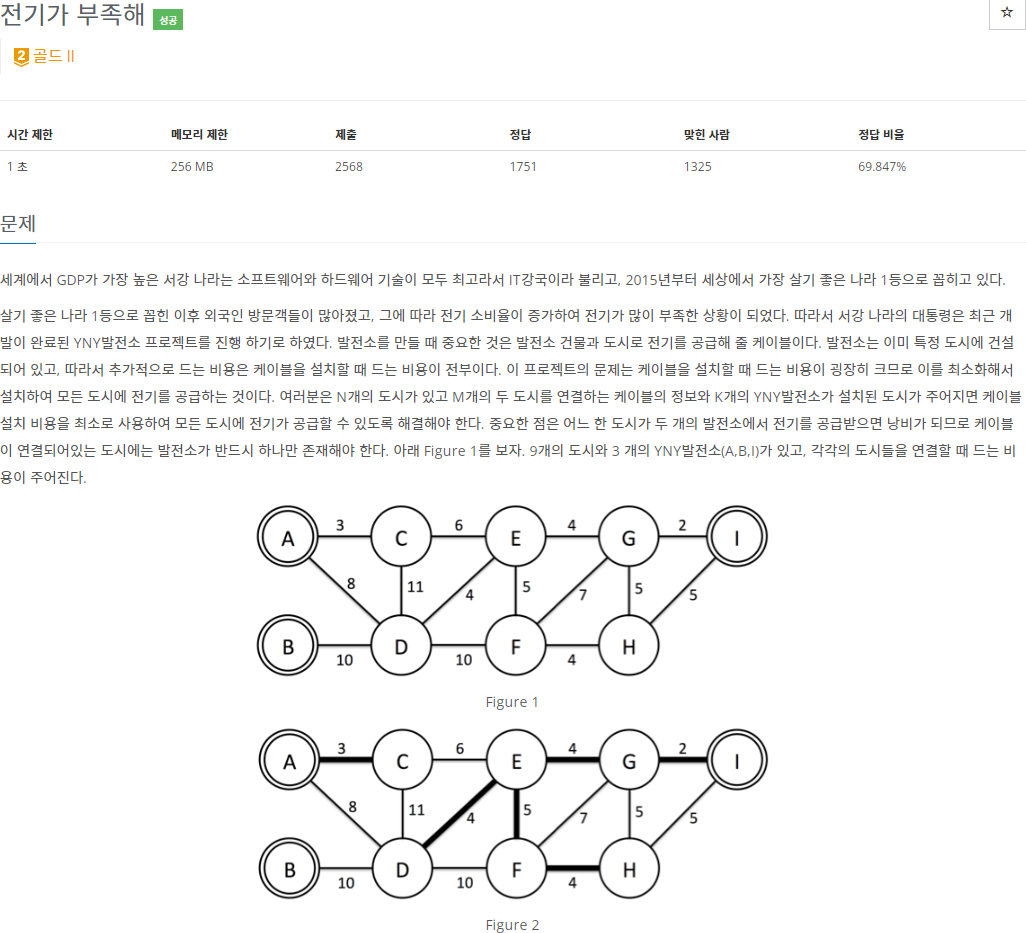
- N개의 도시가 있고 M개의 두 도시를 연결하는 케이블의 정보와 K개의 발전소가 설치된 도시가 주어질 때, 모든 도시에 전기를 공급할 수 있도록 케이블을 설치하는 데에 드는 최소비용을 구하는 문제입니다.
- 입력: 첫 번째 줄에 1보다 크거나 같고 1,000보다 작거나 같은 도시의 개수 N과 1보다 크거나 같고 100,000보다 작거나 같은 설치 가능한 케이블의 수 M이 주어지고 두 번째 줄에 발전소가 설치된 도시의 번호가 주어집니다. 세 번째 줄부터 M개의 줄에 두 도시를 연결하는 케이블의 정보가 u, v, w로 주어집니다. 이는 u 도시와 v 도시를 연결하는 케이블을 설치할 때 w의 비용이 드는 것을 의미합니다.
- w는 10,000보다 작거나 같은 양의 정수입니다.
- 출력: 첫 번째 줄에 모든 도시에 전기를 공급할 수 있도록 케이블을 설치하는 데 드는 최소비용을 출력합니다.
3. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.HashSet;
import java.util.StringTokenizer;
public class Main {
static int N, M, K;
static int[] parents;
static HashSet<Integer> powerPlants;
static int[][] cables;
static void input() {
Reader scanner = new Reader();
N = scanner.nextInt();
M = scanner.nextInt();
K = scanner.nextInt();
powerPlants = new HashSet<>();
parents = new int[N + 1];
cables = new int[M][3];
for(int city = 1; city <= N; city++) parents[city] = city;
for(int city = 0; city < K; city++)
powerPlants.add(scanner.nextInt());
for(int cable = 0; cable < M; cable++) {
int city1 = scanner.nextInt(), city2 = scanner.nextInt(), weight = scanner.nextInt();
cables[cable][0] = city1;
cables[cable][1] = city2;
cables[cable][2] = weight;
}
}
static void solution() {
Arrays.sort(cables, (c1, c2) -> c1[2] - c2[2]);
System.out.println(kruskal());
}
static int kruskal() {
int index = 0, answer = 0;
for(int cableNum = 0; cableNum < N - 1 && index < M; cableNum++) {
if(isConnected()) break;
if(isSameParents(cables[index][0], cables[index][1]) ||
powerPlants.contains(findParent(cables[index][0])) && powerPlants.contains(findParent(cables[index][1]))) {
index++;
cableNum--;
continue;
}
union(cables[index][0], cables[index][1]);
answer += cables[index][2];
index++;
}
return answer;
}
static boolean isConnected() {
for(int city = 1; city <= N; city++)
if(!powerPlants.contains(parents[city])) return false;
return true;
}
static int findParent(int city) {
if(city == parents[city]) return city;
return parents[city] = findParent(parents[city]);
}
static void union(int city1, int city2) {
int parent1 = findParent(city1), parent2 = findParent(city2);
if(parent1 != parent2) {
if(powerPlants.contains(parent1)) parents[parent2] = parent1;
else if(powerPlants.contains(parent2)) parents[parent1] = parent2;
else {
if(parent1 < parent2) parents[parent2] = parent1;
else parents[parent1] = parent2;
}
}
}
static boolean isSameParents(int city1, int city2) {
int parent1 = findParent(city1), parent2 = findParent(city2);
if(parent1 == parent2) return true;
return false;
}
public static void main(String[] args) {
input();
solution();
}
static class Reader {
BufferedReader br;
StringTokenizer st;
public Reader() {
br = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while(st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return st.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
}
}4. 접근
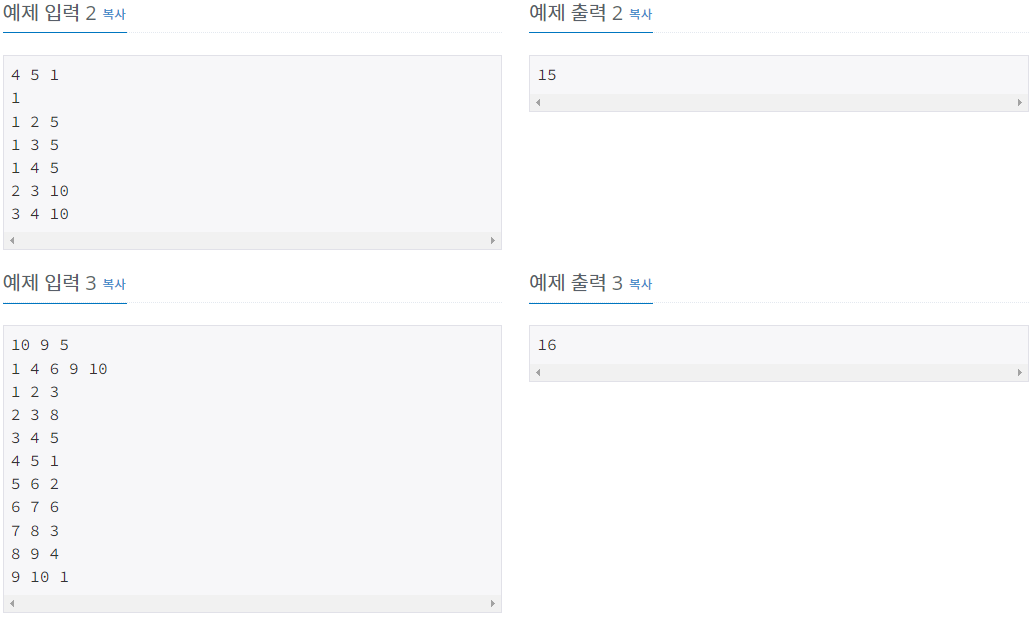
- 최소 신장 트리를 이용하여 최대 N - 1개의 케이블을 선택하여 최소 비용을 구합니다.
- 이 때, 비용이 적은 케이블 순으로 선택하며 최소 신장 트리를 만드는데, 케이블을 하나 선택할 때마다 모든 도시에 전기를 공급할 수 있는지 확인합니다.
- 모든 도시에 전기를 공급할 수 있는지는 최소 신장 트리를 형성하면서 parents라는 배열에 자신의 부모를 저장하는데, 부모들이 모두 발전소에 해당하는지를 보며 확인합니다.
- 만약 모든 부모가 발전소에 해당한다면 모든 도시에 전기를 공급할 수 있다는 뜻이 되므로 이 때는 더이상 케이블을 선택하지 않고 지금까지의 비용의 합을 구하여 반환합니다.