[BaekJoon] 1114 통나무 자르기 (Java)

1.  문제 링크

https://www.acmicpc.net/problem/1114

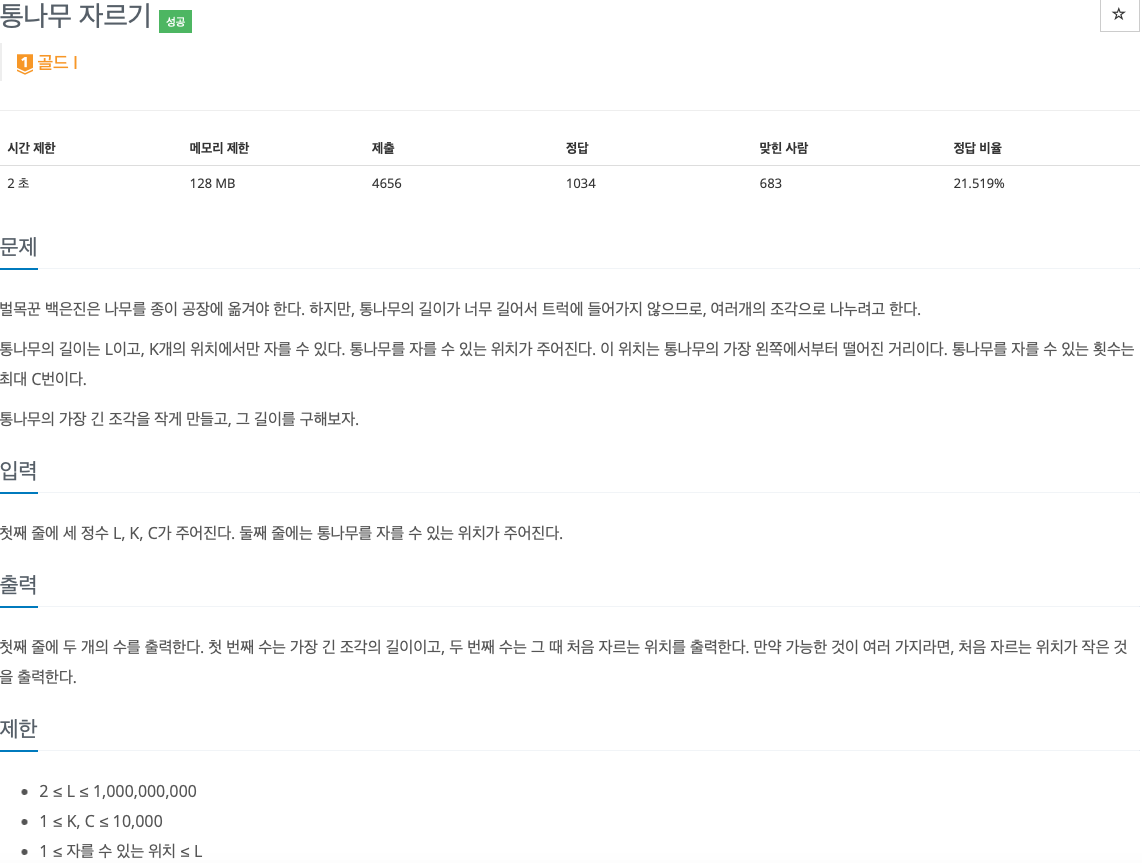
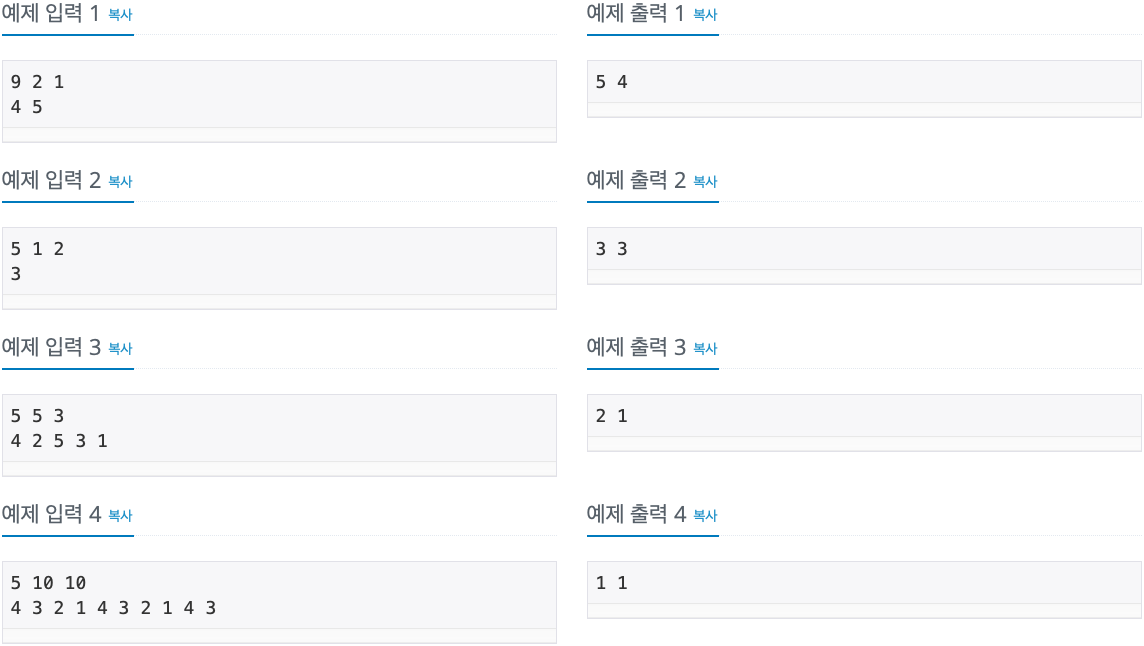
2.  문제

3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.StringTokenizer;

public class Main {
    static int L, K, C, answerLoc, answerLength;
    static List<Integer> cutLocations;

    static void input() {
        Reader scanner = new Reader();

        L = scanner.nextInt();
        K = scanner.nextInt();
        C = scanner.nextInt();
        cutLocations = new ArrayList<>();

        for(int idx = 0; idx < K; idx++)
            cutLocations.add(scanner.nextInt());

        Collections.sort(cutLocations);
    }

    static void solution() {
        // 문제 : 길이 L의 통나무를 K개의 위치에서 최대 C번 잘랐을 때, 통나무의 가장 긴 조각을 가장 작게 만들어라
        // 이를 결정 문제로 바꾸어 길이 L의 통나무를 C번 잘랐을 때, 자른 통나무들의 길이가 모두 특정 길이 이하로 되게 할 수 있는가?로 변경한다
        // 그럼 이 결정 문제는 특정 길이를 이분 탐색을 통해 찾아 해당 길이 이하로 통나무들을 잘라보면 된다
        binarySearch();

        StringBuilder sb = new StringBuilder();
        sb.append(answerLength).append(' ').append(answerLoc);
        System.out.println(sb);
    }

    static void binarySearch() {
        // 왼쪽 포인터는 최소 길이인 1, 오른쪽 포인터는 최대 길이인 L로 두고 이분 탐색을 통해 자른 통나무의 최대 길이를 변경해가며 나무를 잘라본다
        int left = 1, right = L;
        while(left <= right) {
            int mid = (left + right) / 2;
            int minLoc = cutTree(mid); // 이분 탐색을 통해 나온 길이 내로 통나무를 잘라보고 그때 가장 처음 자른 위치를 구한다

            // 만약 현재 길이 내로 통나무를 자를 수 없다면 길이를 늘리기 위해 왼쪽 포인터를 mid + 1로 변경한다
            if(minLoc == 0)
                left = mid + 1;
            else { // 현재 길이 내로 통나무를 자를 수 있다면
                // 최대 길이의 최솟값 및 가장 처음 자른 위치를 갱신하고 길이를 더 줄여보기 위해 오른쪽 포인터를 mid - 1로 변경한다
                answerLength = mid;
                answerLoc = minLoc;
                right = mid - 1;
            }
        }
    }

    // 나무를 자르는 메서드
    static int cutTree(int length) {
        // 처음 자르는 곳의 위치가 최대한 작아야하기 때문에 통나무의 앞부터 자르지 않고 뒤에서부터 자르며
        // 처음 자르는 곳의 위치를 최대한 작게 만든다
        int lastLength = L, count = 0, minLoc = 0;
        // 자르는 곳의 위치는 오름차순으로 정렬되어 있으므로 역순으로 반복문을 돌면서 통나무의 끝부분부터 잘라본다
        // 자를 때에는 length 이하로 통나무들을 자르면 되기 때문에 자르는 부분의 길이가 length보다 커지기 전까지는 위치를 이동시켜보다가
        // length보다 커지면 그 위치 바로 이전에서 통나무를 자른다
        for(int idx = K - 1; idx >= 0; idx--) {
            // 만약 현재 위치에서 자르려고 하는데, 해당 위치부터 통나무 끝까지의 길이가 최대 길이인 length보다 크다면
            if(lastLength - cutLocations.get(idx) > length) {
                // 만약 현재 위치가 자를 수 있는 위치 중 가장 끝 위치라면
                // 가장 끝 위치에서 잘랐는데도 끝까지의 길이가 length보다 크다는 것은 결국 length보다 큰 조각이 최소 한 개는 존재한다는 뜻이 된다
                // 그러므로 이러한 경우에는 자를 수 없음을 나타내기 위해 0을 반환한다
                if(idx == K - 1) return 0;
                // 현재 위치에서 자르면 length보다 크기 때문에 바로 이전의 자를 수 있는 위치에서 통나무를 잘라야 한다
                // 그러므로 바로 이전의 위치에서 자르고 난 이후에 남은 통나무의 길이는 바로 이전의 위치만큼이 된다
                // lastLength의 값을 바로 이전 위치로 변경한다
                lastLength = cutLocations.get(idx + 1);
                // 그렇다면 남은 통나무에 대해서는 현재 위치가 자를 수 있는 가장 긴 위치가 될테니
                // 마찬가지로 남은 통나무를 현재 위치에서 잘랐을 때 length보다 크다면 length보다 큰 조각이 최소 한 개 이상 존재할테니
                // 이 경우는 자를 수 없음을 나타내기 위해 0을 반환한다
                if(lastLength - cutLocations.get(idx) > length) return 0;
                // 위 과정을 거쳤다면 통나무를 자른 과정이 진행된 것이므로 자른 횟수를 1 증가시킨다
                count++;
                // 그리고 처음 자른 위치의 값을 갱신해나간다
                minLoc = cutLocations.get(idx + 1);
            }

            if(count >= C) break;
        }

        // 만약 위 반복문을 돌면서 C번만큼 통나무를 자르지 않았다면
        // 아직 자를 수 있는 횟수가 남아있기 때문에 자를 수 있는 위치의 가장 앞에서 한 번 더 잘라도 된다
        // 그러므로 처음 자른 위치의 값을 자를 수 있는 위치의 가장 앞으로 변경한다
        if(count < C) minLoc = cutLocations.get(0);

        // 만약 처음 자른 위치의 값이 length를 넘는다면, 처음 자른 통나무의 길이가 length를 넘는다는 뜻이므로
        // length보다 긴 조각이 존재한다는 뜻이기 때문에 자를 수 없음을 나타내기 위해 0을 반환한다
        if(minLoc > length) return 0;
        // 위 경우를 모두 지나왔다면 현재 length 길이 내로 자를 수 있는 상황임을 나타내는 것이기 때문에
        // 처음 자른 위치의 값을 반환한다
        return minLoc;
    }

    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;

        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }

        String next() {
            while(st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }

            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }
    }
}