[BaekJoon] 11780 플로이드 2 (Java)

1.  문제 링크

https://www.acmicpc.net/problem/11780

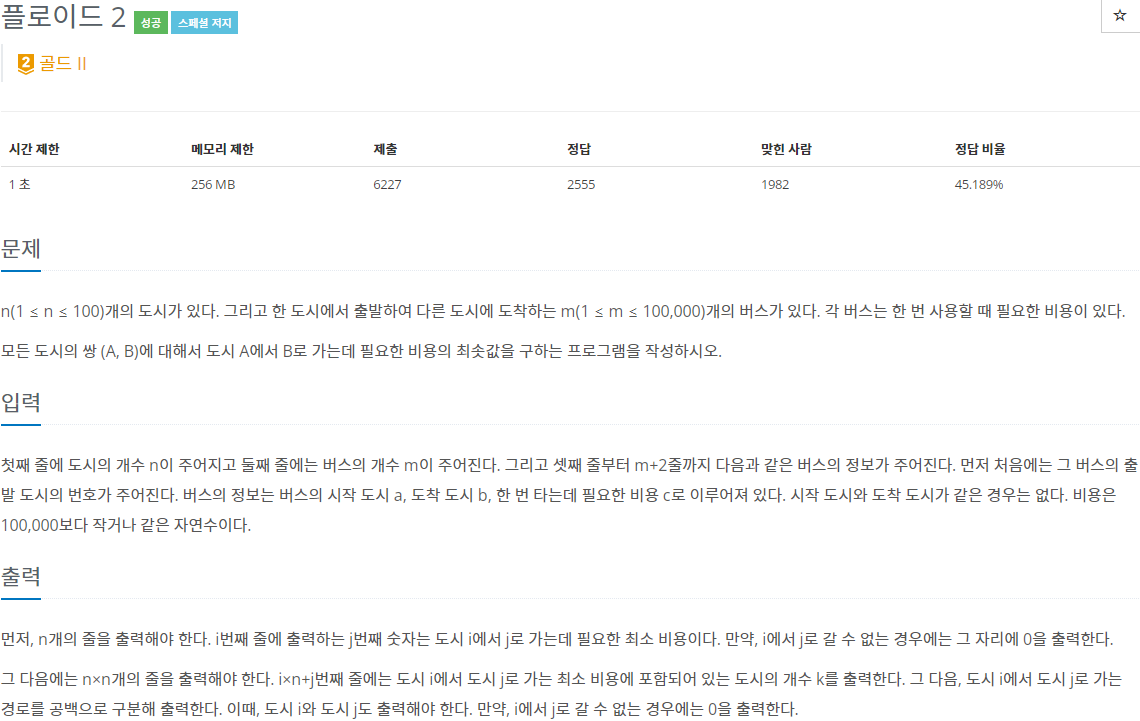
2.  문제

요약

• n개의 도시가 있고 한 도시에서 출발하여 다른 도시에 도착하는 m개의 버스가 있습니다.
• 각 버스는 한 번 사용할 때 필요한 비용이 있습니다.
• 모든 도시의 쌍 (A, B)에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구하는 문제입니다.
• 입력: 첫 번째 줄에 1보다 크거나 같고 100보다 작거나 같은 도시의 개수 n이 주어지고 두 번째 줄에 1보다 크거나 같고 100,000보다 작거나 같은 버스의 개수 m이 주어지며, 세 번째 줄부터 m개의 줄에 버스의 정보가 주어집니다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필욯란 비용 c로 이루어져 있습니다.
  • 시작 도시와 도착 도시가 같은 경우는 없습니다.
  • 비용은 100,000보다 작거나 같은 자연수입니다.
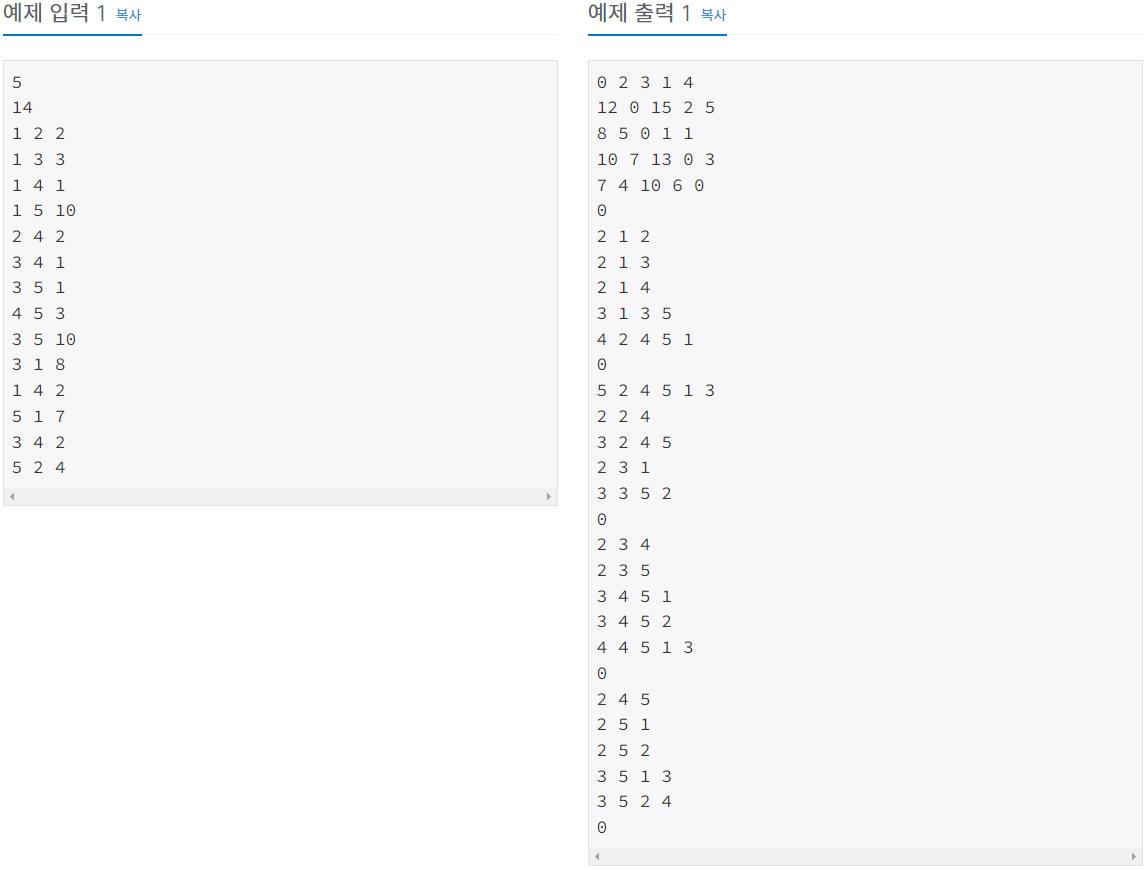
• 출력: n개의 줄을 출력합니다. i번째 줄에 출력하는 j번째 숫자는 도시 i에서 j로 가는데 필요한 최소 비용입니다. 만약 i에서 j로 갈 수 없는 경우에는 그 자리에 0을 출력합니다. 그 다음에는 n x n개의 줄을 출력합니다. i x n + j 번째 줄에는 도시 i에서 도시 j로 가는 최소 비용에 포함되어 있는 도시의 개수 k를 출력하고 도시 i에서 도시 j로 가는 경로를 출력합니다. 이 때, 도시 i와 도시 j도 출력해야 합니다. 만약 i에서 j로 갈 수 없는 경우에는 0을 출력합니다.

3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    static StringBuilder sb = new StringBuilder();
    static int n, m;
    static long[][] costs;
    static int[][] path;

    static void input() {
        Reader scanner = new Reader();

        n = scanner.nextInt();
        m = scanner.nextInt();
        costs = new long[n + 1][n + 1];
        path = new int[n + 1][n + 1];
        for(int row = 0; row <= n; row++) {
            for(int col = 0; col <= n; col++) {
                path[row][col] = -1;
                if(row == col) costs[row][col] = 0;
                else costs[row][col] = Long.MAX_VALUE;
            }
        }

        for(int edge = 0; edge < m; edge++) {
            int start = scanner.nextInt(), end = scanner.nextInt(), cost = scanner.nextInt();

            if(costs[start][end] > cost)
                costs[start][end] = cost;
            path[start][end] = start;
        }
    }

    static void solution() {
        floydWarshall(costs);

        print(costs, path);
        System.out.print(sb);
    }

    static void print(long[][] costs, int[][] path) {
        printCosts(costs);
        printPaths(path);
    }

    static void printCosts(long[][] costs) {
        for(int row = 1; row <= n; row++) {
            for(int col = 1; col <= n; col++) {
                if(costs[row][col] == Long.MAX_VALUE) sb.append(0).append(' ');
                else sb.append(costs[row][col]).append(' ');
            }
            sb.append('\n');
        }
    }

    static void printPaths(int[][] path) {
        for(int row = 1; row <= n; row++) {
            for(int col = 1; col <= n; col++) {
                if(path[row][col] == -1)
                    sb.append(0).append('\n');
                else {
                    Stack<Integer> pathStack = new Stack<>();
                    int pre = col;
                    pathStack.push(col);

                    while(row != path[row][pre]) {
                        pre = path[row][pre];
                        pathStack.push(pre);
                    }

                    sb.append((pathStack.size() + 1)).append(' ');

                    sb.append(row).append(' ');
                    while(!pathStack.isEmpty()) {
                        sb.append(pathStack.pop()).append(' ');
                    }
                    sb.append('\n');
                }
            }
        }
    }

    static void floydWarshall(long[][] costs) {
        for(int middle = 1; middle <= n; middle++) {
            for(int start = 1; start <= n; start++) {
                for(int end = 1; end <= n; end++) {
                    if(middle == start) continue;
                    if(start == end) continue;
                    if(middle == end) continue;

                    if(costs[start][middle] == Long.MAX_VALUE || costs[middle][end] == Long.MAX_VALUE) continue;

                    if(costs[start][end] > costs[start][middle] + costs[middle][end]) {
                        costs[start][end] = costs[start][middle] + costs[middle][end];
                        path[start][end] = path[middle][end];
                    }
                }
            }
        }
    }

    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;

        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }

        String next() {
            while(st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }

            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }
    }
}

4.  접근

• 최대 100개의 도시에서 최대 100,000개의 버스가 있기 때문에 사이클이 발생할 수 있어 다익스트라 알고리즘은 사용하지 못합니다.
• 플로이드-워셜 알고리즘을 이용해서 최소 비용을 구합니다.

• 주어진 버스 정보를 2차원 배열 costs에 저장하는데, 이 때 costs[i][j]는 i번 도시에서 j번 도시로 가는 데에 필요한 비용을 나타내고 만약 i번 도시에서 j번 도시로 가는 경로가 여러 개라면 그 중 가장 비용이 적은 것으로 기록합니다.
• path라는 2차원 배열도 생성하는데, path[i][j]는 i번 도시에서 j번 도시로 가는 데에 j번 도시 바로 전에 거친 도시를 나타냅니다. 처음에는 모든 값을 -1로 초기화합니다.
• 플로이드-워셜 알고리즘을 통해 한 도시에서 각 도시로의 최소 비용을 구하는데, 이 때 path 배열 값을 변경하면서 i번 도시에서 j번 도시로 가는 경로를 구합니다.
  • start번 도시에서 end번 도시로 갈 때, middle번 도시를 거쳐 가는 비용을 계산하여 만약 그 비용이 costs[start][end]보다 적다면 costs[start][end]의 값을 계산한 비용으로 갱신하고 path[start][end]의 값을 path[middle][end] 값으로 갱신합니다.
• 플로이드-워셜 알고리즘을 통해 구한 costs 배열과 path 배열을 이용하여 출력 형식에 맞게 출력합니다.
  • 경로를 출력할 때는 path[i][j] 값이 -1이라면 i번 도시에서 j번 도시로 갈 수 없다는 뜻이므로 0을 출력합니다.
  • 만약 그렇지 않다면 pre라는 변수를 값을 j로 초기화하고 Stack에 pre 값을 넣어 초기화를 한 후에 i와 path[i][pre]의 값이 같아지기 전까지 pre 값을 path[i][pre] 값으로 갱신해나가면서 Stack에 pre 값을 넣습니다.
  • 다 넣은 후에는 i번부터 Stack에 있는 수를 pop하면서 경로를 출력합니다.