1. 문제 링크
https://www.acmicpc.net/problem/12763
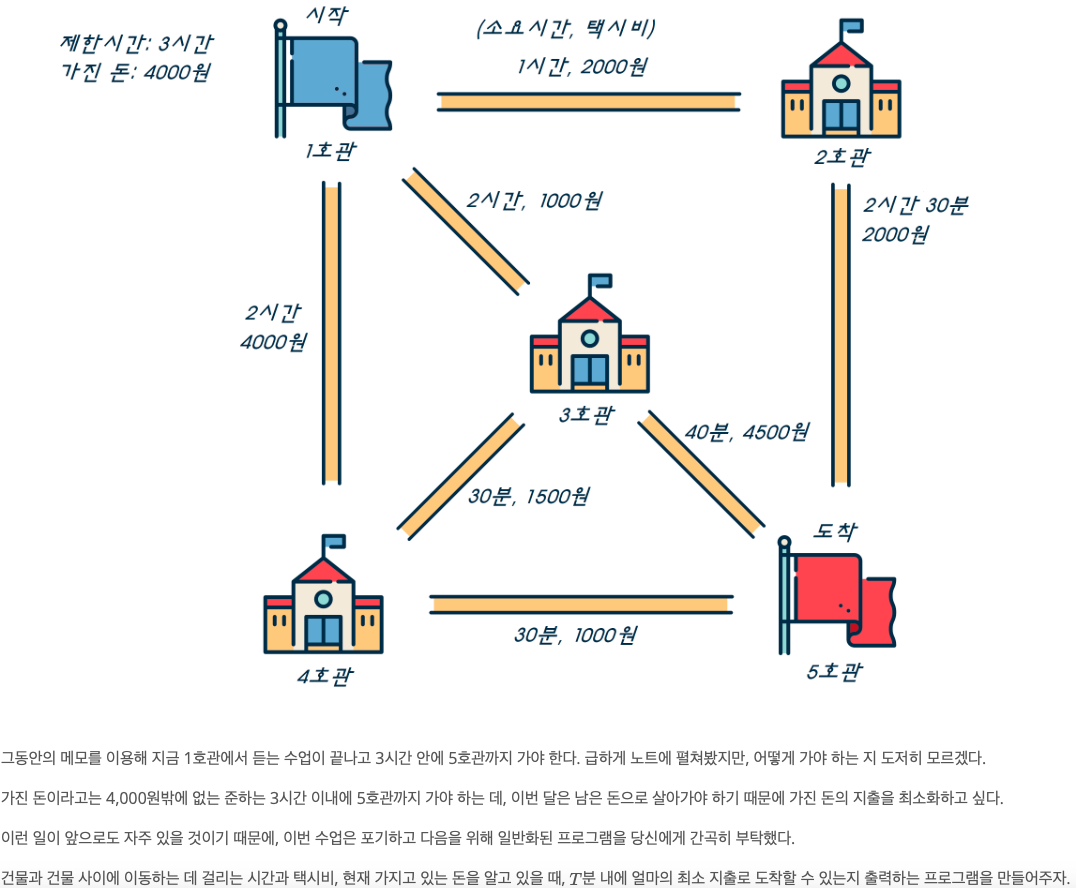
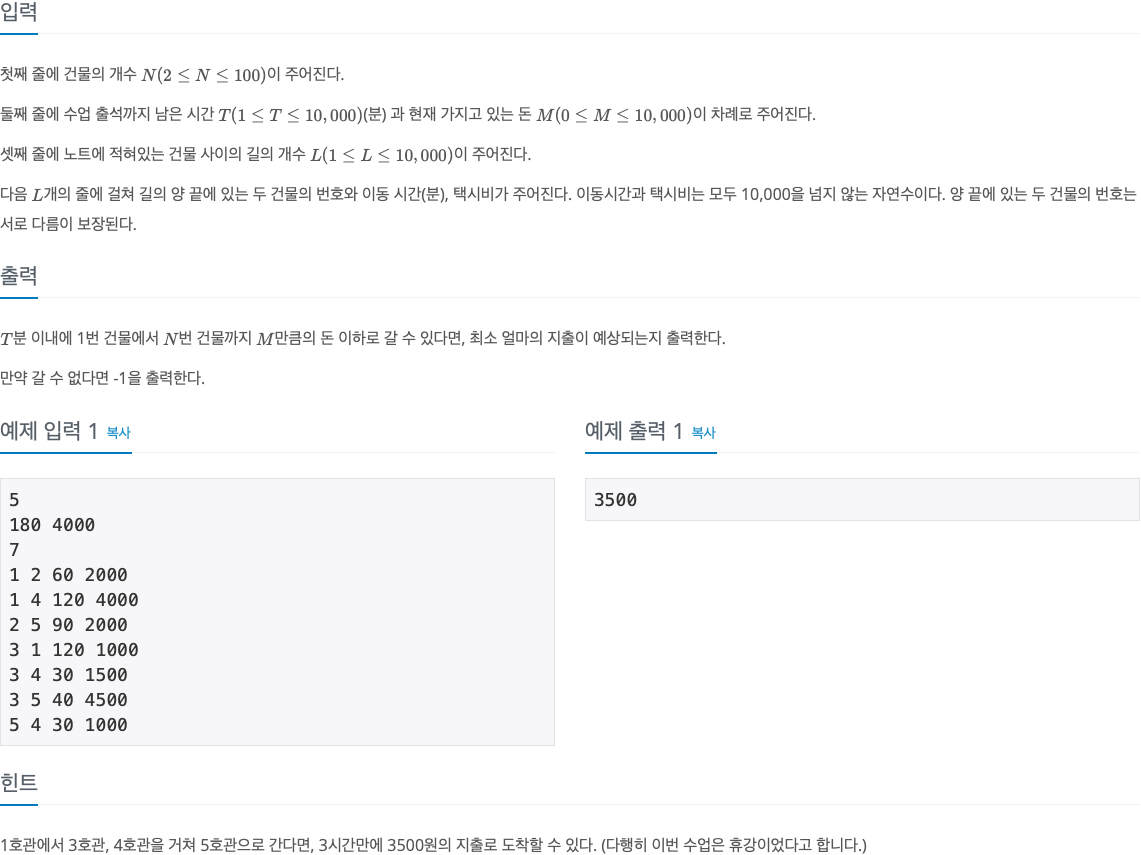
2. 문제

3. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int buildingCount;
static int deadline;
static int money;
static int roadCount;
static Map<Integer, List<Road>> roads;
static void input() {
Reader scanner = new Reader();
buildingCount = scanner.nextInt();
deadline = scanner.nextInt();
money = scanner.nextInt();
roadCount = scanner.nextInt();
roads = new HashMap<>();
for (int building = 1; building <= buildingCount; building++) {
roads.put(building, new ArrayList<>());
}
for (int road = 1; road <= roadCount; road++) {
int building1 = scanner.nextInt();
int building2 = scanner.nextInt();
int time = scanner.nextInt();
int fee = scanner.nextInt();
roads.get(building1).add(new Road(building2, time, fee));
roads.get(building2).add(new Road(building1, time, fee));
}
}
/*
* 다익스트라를 이용하여 최소 비용을 구한다
*
* 문제에서 주어진 조건은 주어진 시간 내에 가지고 있는 돈을 가지고 1번 건물에서 N번 건물까지 이동하는 것이다
* 그러므로 다익스트라 알고리즘을 수행할 때 1차원 배열을 통해 최소 비용을 구할 수는 없다
* - 각 건물에 몇 분을 걸려 도착했는지에 따라 각 건물에서의 최소 비용이 달라지기 때문에 건물의 번호와 시간을 이용하여 최소 비용 배열을 2차원 배열로 만든다
* - 시간은 주어진 시간인 T 이하의 시간으로 N번 건물까지 도착해야 하기 때문에 2차원 배열에서 시간에 해당하는 행/열의 크기는 T + 1이 된다
*
* 위와 같이 최소 비용 배열을 정의한 후에 일반 다익스트라 알고리즘과 같이 시작 건물부터 시작하여 연결된 다른 건물들로 이동하며 최소 비용을 구한다
* - 다음 건물로 이동했을 때의 시간과 비용을 계산하여 주어진 시간과 비용 내에 있는지 확인한다
* - 그렇다면 이동할 수 있는 상황이기 때문에 다음 건물을 계산한 시간에 도착했을 때의 최소 비용과 계산한 비용을 비교하여 최소 비용이 더 크다면 최소 비용을 갱신한다
*/
static void solution() {
int minFee = dijkstra(1, buildingCount);
System.out.println(minFee == Integer.MAX_VALUE ? -1 : minFee);
}
static int dijkstra(int startBuilding, int endBuilding) {
Queue<Road> queue = new PriorityQueue<>();
int[][] fee = new int[buildingCount + 1][deadline + 1];
for (int building = 1; building <= buildingCount; building++) {
if (building == startBuilding) {
continue;
}
Arrays.fill(fee[building], Integer.MAX_VALUE);
}
queue.offer(new Road(startBuilding, 0, 0));
fee[startBuilding][0] = 0;
while (!queue.isEmpty()) {
Road cur = queue.poll();
if (fee[cur.building][cur.time] < cur.taxiFee) {
continue;
}
for (Road next : roads.get(cur.building)) {
int nextBuilding = next.building;
int nextFee = cur.taxiFee + next.taxiFee;
int nextTime = cur.time + next.time;
if (nextTime > deadline || nextFee > money) {
continue;
}
if (fee[nextBuilding][nextTime] > nextFee) {
fee[nextBuilding][nextTime] = nextFee;
queue.offer(new Road(nextBuilding, nextTime, nextFee));
}
}
}
return Arrays.stream(fee[endBuilding]).filter(taxiFee -> taxiFee != 0).min().getAsInt();
}
static class Road implements Comparable<Road> {
int building;
int time;
int taxiFee;
public Road(int building, int time, int taxiFee) {
this.building = building;
this.time = time;
this.taxiFee = taxiFee;
}
@Override
public int compareTo(Road o) {
if (taxiFee != o.taxiFee) {
return taxiFee - o.taxiFee;
}
return time - o.time;
}
}
public static void main(String[] args) {
input();
solution();
}
static class Reader {
BufferedReader br;
StringTokenizer st;
public Reader() {
br = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while (st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return st.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
}
}
