[BaekJoon] 13418 학교 탐방하기 (Java)

1.  문제 링크

https://www.acmicpc.net/problem/13418

2.  문제

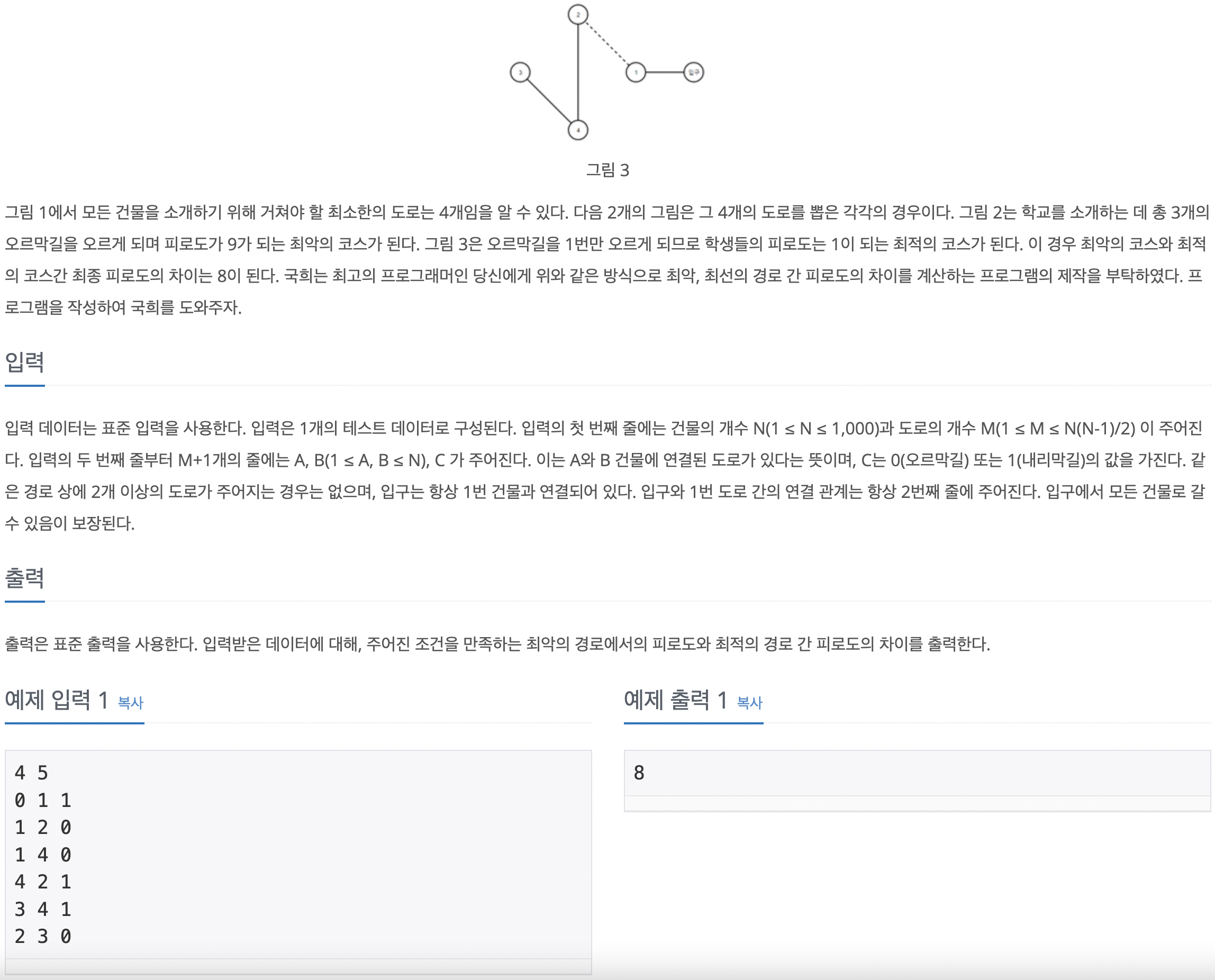
요약

• 학교 건물을 차례로 소개할 수 있는 이동 경로를 짜보기로 하였는데, 건물 간 연결된 길이 오르막길일 수도 있고, 내리막길일 수도 있습니다.
• 건물을 방문하는 데에 필요한 최소한의 길을 선택하여 해당 길을 통해서만 건물들을 소개하기로 하였는데, 오르막길이 많이 포함되게 되면 피곤해지기 때문에 피로도를 계산하여 경로를 정하려고 합니다.
• 오르막길을 k번 오를 때, 피로도는 $k^2$이 되고, 피로도의 계산은 최초 조사된 길을 기준으로만 합니다. 즉, 내리막길로 내려갔다 다시 올라올 때 오르막길이 되는 경우는 고려하지 않습니다.
• 입구는 항상 1번 건물과 연결된 도로를 가지고, 출발은 항상 입구에서 합니다.
• 각 건물 사이에 연결된 길이 주어질 때, 최악, 최선의 경로 간 피로도의 차이를 계산하는 문제입니다.
• 입력: 첫 번째 줄에 1보다 크거나 같고 1,000보다 작거나 같은 건물의 개수 N과 1보다 크거나 같고 N(N - 1)/2보다 작거나 같은 도로의 개수 M이 주어지고 두 번째 줄부터 M + 1개의 줄에 1보다 크거나 같고 N보다 작거나 같은 A, B와 C가 주어집니다. 이는 A와 B 건물에 연결된 도로가 있다는 뜻이며, C는 0(오르막길) 또는 1(내리막길)의 값을 가집니다.
  • 같은 경로 상에 2개 이상의 도로가 주어지는 경우는 없고, 입구는 항상 1번 건물과 연결되어 있습니다.
  • 입구와 1번 도로 간의 연결 관계는 항상 2번째 줄에 주어집니다.
  • 입구에서 모든 견물로 갈 수 있음이 보장됩니다.
• 출력: 첫 번째 줄에 최악의 경로에서의 피로도와 최적의 경로 간 피로도의 차이를 출력합니다.

3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    static int N, M;
    static int[][] roads;
    static int[] parents;

    static void input() {
        Reader scanner = new Reader();

        N = scanner.nextInt();
        M = scanner.nextInt();
        roads = new int[M + 1][3];
        parents = new int[N + 1];

        roads[0][0] = scanner.nextInt();
        roads[0][1] = scanner.nextInt();
        roads[0][2] = scanner.nextInt();

        for(int road = 1; road <= M; road++) {
            int start = scanner.nextInt(), end = scanner.nextInt(), isUphill = scanner.nextInt();
            roads[road][0] = start;
            roads[road][1] = end;
            roads[road][2] = isUphill;
        }
    }

    static void solution() {
        for(int building = 0; building <= N; building++)
            parents[building] = building;
        Arrays.sort(roads, (road1, road2) -> road1[2] - road2[2]);
        int max = kruskal();

        for(int building = 0; building <= N; building++)
            parents[building] = building;
        Arrays.sort(roads, (road1, road2) -> road2[2] - road1[2]);
        int min = kruskal();

        System.out.println(max - min);
    }

    static int kruskal() {
        int upHillNum = 0;

        int index = 0;
        for(int roadNum = 0; roadNum < N; roadNum++) {
            int[] road = roads[index];
            if(isSameParents(road[0], road[1])) {
                roadNum--;
            } else {
                union(road[0], road[1]);
                if(road[2] == 0) upHillNum++;
            }
            index++;
        }

        return (int)Math.pow(upHillNum, 2);
    }

    static int findParent(int building) {
        if(building == parents[building]) return building;
        return parents[building] = findParent(parents[building]);
    }

    static void union(int building1, int building2) {
        int parent1 = findParent(building1), parent2 = findParent(building2);

        if(parent1 != parent2) {
            if(parent1 < parent2) parents[parent2] = parent1;
            else parents[parent1] = parent2;
        }
    }

    static boolean isSameParents(int building1, int building2) {
        int parent1 = findParent(building1), parent2 = findParent(building2);

        if(parent1 == parent2) return true;
        return false;
    }

    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;

        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }

        String next() {
            while(st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }

            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }
    }
}

4.  접근

• 건물을 방문하는 데에 필요한 최소한의 길을 선택하여 이동하려고 하기 때문에 최소 스패닝 트리를 이용할 수 있습니다.
• 즉, 주어진 도로에서 사이클이 발생하지 않는 N - 1개의 도로를 선택하면 됩니다.
• 이 때, 최적의 경로는 최대한 내리막길을 많이 이용하고, 최악의 경로는 최대한 오르막길을 많이 이용하면 됩니다.
• 그러므로 최소 스패닝 트리를 만들기 위해 크루스칼 알고리즘을 사용하는데,
  • 최적의 경로는 먼저 내리막길을 이용해서 최소 스패닝 트리를 만들고, N - 1개의 길이 선택되지 않았을 때 오르막길을 이용합니다.
  • 최악의 경로는 먼저 오르막길을 이용해서 최소 스패닝 트리를 만들고, N - 1개의 길이 선택되지 않았을 때 내리막길을 이용합니다.
• 위와 같이 진행하기 위해 크루스칼 알고리즘을 진행할 때 길을 다음과 같이 정렬합니다.
  • 최적의 경로에서는 내리막길을 우선 나오게, 오르막길을 뒤에 나오게 정렬합니다.
  • 최악의 경로에서는 오르막길을 우선 나오게, 내리막길을 뒤에 나오게 정렬합니다.
• 위와 같이 길을 정렬한 후에 각각에 대해 크루스칼 알고리즘을 적용하여 경로에 포함되는 오르막길의 개수를 각각 구하고 각 개수의 제곱에 대한 차를 구하면 해당 문제의 답을 찾을 수 있습니다.