1. 문제 링크
https://www.acmicpc.net/problem/13460
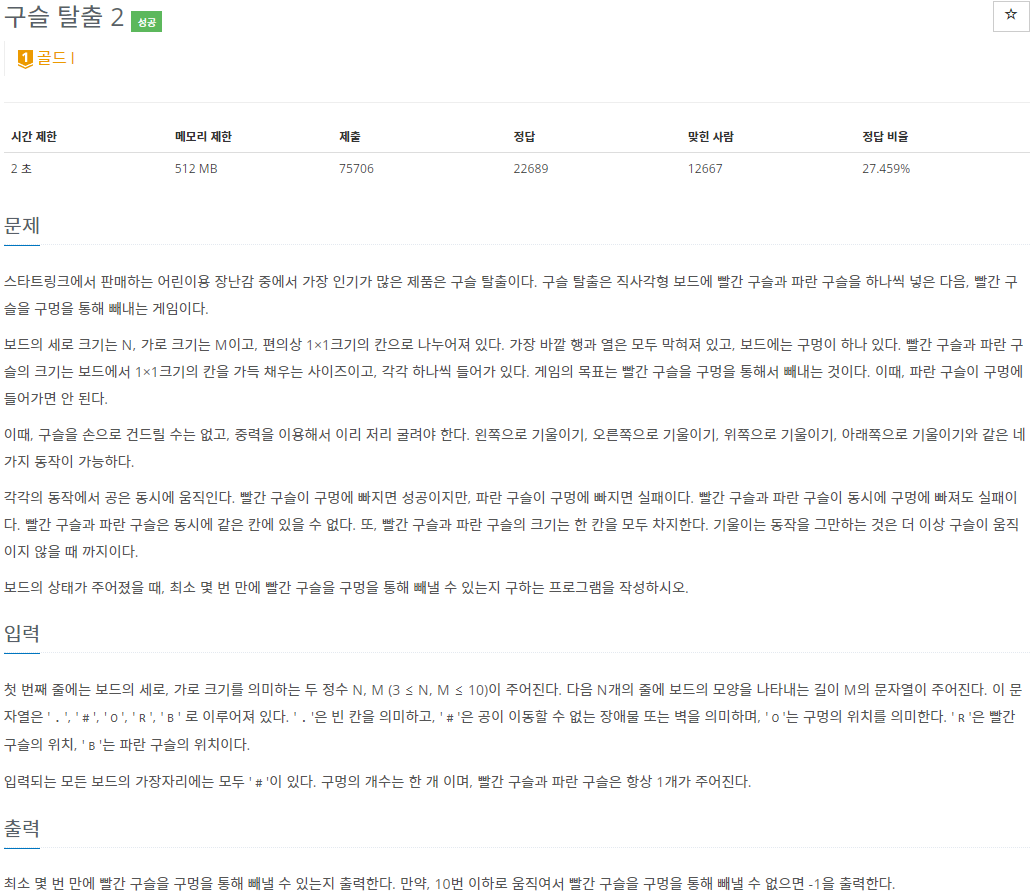
2. 문제
요약
- 구슬 탈출은 직사각형 보드에 빨간 구슬과 파란 구슬을 하나씩 넣은 다음, 빨간 구슬을 구멍을 통해 빼내는 게임입니다.
- 보드의 세로 크기는 N, 가로 크기는 M이고, 편의상 1 x 1 크기의 칸으로 나누어져 있습니다.
- 가장 바깥 행과 열은 모두 막혀있고, 보드에는 구멍이 하나 있습니다.
- 빨간 구슬과 파란 구슬의 크기는 1 x 1 칸을 가득 채우는 사이즈이고, 각각 하나씩 들어가있는데, 목표는 파란 구슬이 구멍에 들어가지 않으면서 빨간 구슬을 구멍을 통해서 빼내는 것입니다.
- 구슬을 손으로 건드릴 수는 없고, 중력을 이용해서 굴려야 합니다.
- 왼쪽으로 기울이기, 오른쪽으로 기울이기, 위쪽으로 기울이기, 아래쪽으로 기울이기와 같은 네 가지 동작이 가능합니다.
- 각 동작에서 공은 동시에 움직이는데, 빨간 구슬이 구멍에 빠지면 성공이지만 파란 구슬이 구멍에 빠지면 실패입니다. 빨간 구슬과 파란 구슬이 동시에 구멍에 빠지더라도 실패입니다.
- 기울이는 동작을 그만하는 것은 더 이상 구슬이 움직이지 않을 때까지입니다.
- 보드의 상태가 주어졌을 때, 최소 몇 번만에 빨간 구슬을 구멍을 통해 빼낼 수 있는지 구하는 문제입니다.
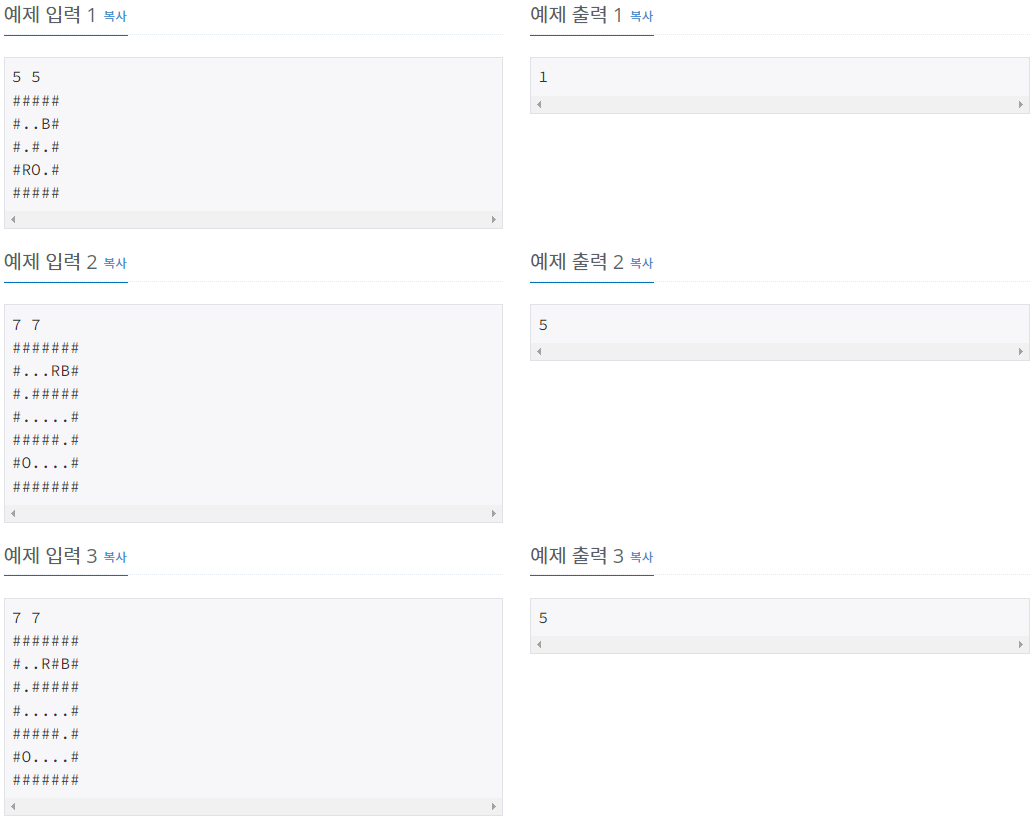
- 입력: 첫 번째 줄에 3보다 크거나 같고 10보다 작거나 같은 보드의 세로 크기 N과 가로 크기 M이 주어지고 두 번째 줄부터 N개의 줄에 보드의 모양을 나타내는 길이가 M인 문자열이 주어집니다. 문자열은 '.', '#', 'O', 'R', 'B'로 이루어져 있는데, '.'은 빈 칸을, '#'은 공이 이동할 수 없는 장애물 또는 벽을, 'O'는 구멍의 위치를, 'R'은 빨간 구슬의 위치를, 'B'는 파란 구슬의 위치를 의미합니다.
- 입력되는 모든 보드의 가장자리에는 모두 '#'이 있습니다.
- 구멍의 개수는 한 개이며, 빨간 구슬과 파란 구슬은 항상 1개가 주어집니다.
- 출력: 첫 번째 줄에 최소 몇 번 만에 빨간 구슬을 구멍을 통해 빼낼 수 있는지를 출력합니다. 만약 10번 이하로 움직여서 빨간 구슬을 구멍을 통해 빼낼 수 없으면 -1을 출력합니다.
3. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int N, M;
static char[][] map;
static Turn init;
static int[] hole;
static void input() {
Reader scanner = new Reader();
N = scanner.nextInt();
M = scanner.nextInt();
map = new char[N][M];
int[] red = null, blue = null;
for(int row = 0; row < N; row++) {
String info = scanner.nextLine();
for(int col = 0; col < M; col++) {
map[row][col] = info.charAt(col);
if(map[row][col] == 'O') hole = new int[] {row, col};
else if(map[row][col] == 'R') {
map[row][col] = '.';
red = new int[] {row, col};
} else if(map[row][col] == 'B') {
map[row][col] = '.';
blue = new int[] {row, col};
}
}
}
init = new Turn(red, blue);
}
static void solution() {
System.out.println(bfs(init));
}
static int bfs(Turn init) {
boolean[][][][] visited = new boolean[N][M][N][M];
Queue<Turn> queue = new LinkedList<>();
queue.offer(init);
while(!queue.isEmpty()) {
Turn cur = queue.poll();
if(map[cur.red[0]][cur.red[1]] == 'O' && map[cur.blue[0]][cur.blue[1]] != 'O') return cur.moveNum;
else if(map[cur.blue[0]][cur.blue[1]] == 'O') continue;
int[] red = cur.red, blue = cur.blue;
for(int dir = 0; dir < 4; dir++) {
int[] tempRed = null, tempBlue = null;
if(dir == 0) {
tempRed = moveLeft(red);
tempBlue = moveLeft(blue);
if(map[tempRed[0]][tempRed[1]] == 'O' && map[tempBlue[0]][tempBlue[1]] == 'O') continue;
if(tempRed[0] == tempBlue[0] && tempRed[1] == tempBlue[1]) {
if(red[1] > blue[1]) tempRed[1]++;
else tempBlue[1]++;
}
} else if(dir == 1) {
tempRed = moveRight(red);
tempBlue = moveRight(blue);
if(map[tempRed[0]][tempRed[1]] == 'O' && map[tempBlue[0]][tempBlue[1]] == 'O') continue;
if(tempRed[0] == tempBlue[0] && tempRed[1] == tempBlue[1]) {
if(red[1] > blue[1]) tempBlue[1]--;
else tempRed[1]--;
}
} else if(dir == 2) {
tempRed = moveUp(red);
tempBlue = moveUp(blue);
if(map[tempRed[0]][tempRed[1]] == 'O' && map[tempBlue[0]][tempBlue[1]] == 'O') continue;
if(tempRed[0] == tempBlue[0] && tempRed[1] == tempBlue[1]) {
if(red[0] > blue[0]) tempRed[0]++;
else tempBlue[0]++;
}
} else if(dir == 3) {
tempRed = moveDown(red);
tempBlue = moveDown(blue);
if(map[tempRed[0]][tempRed[1]] == 'O' && map[tempBlue[0]][tempBlue[1]] == 'O') continue;
if(tempRed[0] == tempBlue[0] && tempRed[1] == tempBlue[1]) {
if(red[0] > blue[0]) tempBlue[0]--;
else tempRed[0]--;
}
}
if(visited[tempRed[0]][tempRed[1]][tempBlue[0]][tempBlue[1]]) continue;
if(cur.moveNum + 1 > 10) continue;
visited[tempRed[0]][tempRed[1]][tempBlue[0]][tempBlue[1]] = true;
queue.offer(new Turn(tempRed, tempBlue, cur.moveNum + 1));
}
}
return -1;
}
static int[] moveLeft(int[] loc) {
for(int col = loc[1]; col >= 0; col--) {
if(map[loc[0]][col] == 'O') return new int[] {loc[0], col};
if(map[loc[0]][col] == '#') return new int[] {loc[0], col + 1};
}
return new int[] {loc[0], 0};
}
static int[] moveRight(int[] loc) {
for(int col = loc[1]; col < M; col++) {
if(map[loc[0]][col] == 'O') return new int[] {loc[0], col};
if(map[loc[0]][col] == '#') return new int[] {loc[0], col - 1};
}
return new int[] {loc[0], M - 1};
}
static int[] moveUp(int[] loc) {
for(int row = loc[0]; row >= 0; row--) {
if(map[row][loc[1]] == 'O') return new int[] {row, loc[1]};
if(map[row][loc[1]] == '#') return new int[] {row + 1, loc[1]};
}
return new int[] {0, loc[1]};
}
static int[] moveDown(int[] loc) {
for(int row = loc[0]; row < N; row++) {
if(map[row][loc[1]] == 'O') return new int[] {row, loc[1]};
if(map[row][loc[1]] == '#') return new int[] {row - 1, loc[1]};
}
return new int[] {N - 1, loc[1]};
}
static class Turn {
int[] red, blue;
int moveNum;
public Turn(int[] red, int[] blue) {
this.red = red;
this.blue = blue;
moveNum = 0;
}
public Turn(int[] red, int[] blue, int moveNum) {
this.red = red;
this.blue = blue;
this.moveNum = moveNum;
}
}
public static void main(String[] args) {
input();
solution();
}
static class Reader {
BufferedReader br;
StringTokenizer st;
public Reader() {
br = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while(st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return st.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
String nextLine() {
String str = "";
try {
str = br.readLine();
} catch (IOException e) {
e.printStackTrace();
}
return str;
}
}
}4. 접근
- 각 동작들을 나타내기 위해 Turn 클래스를 정의합니다.
- 빨간색 공의 위치를 나타내는 배열 red, 파란색 공의 위치를 나타내는 배열 blue, 현재 동작까지 수행한 동작의 횟수를 나타내는 변수 moveNum을 멤버 변수로 가집니다.
- BFS를 통해 빨간색 공과 파란색 공을 이동시켜보며 빨간 구슬을 구멍을 통해 빼낼 수 있는 최소 횟수를 찾습니다.
- 방문 체크를 진행할 때는, 빨간색 공과 파란색 공이 같이 움직이기 때문에 각 공을 따로 볼 수 없으므로 각 공의 위치를 합쳐 방문 체크를 진행합니다.
- 그러므로 방문 체크를 진행하는 visited 배열은 visited[빨간 공의 행의 좌표][빨간 공의 열의 좌표][파란 공의 행의 좌표][파란 공의 열의 좌표]를 나타내도록 만듭니다.
- 만약 현재 탐색하는 두 공의 위치를 봤을 때 파란색 공이 구멍에 위치하고 있다면 해당 경우는 잘못된 경우이므로 제외하고 다른 경우를 탐색합니다.
- 각 동작에서 왼쪽, 오른쪽, 위쪽, 아래쪽으로 빨간색 공과 파란색 공을 굴립니다.
- 각 기울이는 동작은 장애물을 만나거나 구멍을 만날 때까지 이동하다 장애물을 만나면 그 직전에, 구멍을 만나면 구멍의 위치에 멈춥니다.
- 굴린 후에 두 공이 모두 구멍에 위치한다면 두 공 모두 빠져나갈 수 있다는 뜻이므로 이러한 경우는 제외하고 다음 경우를 살펴봅니다.
- 만약 두 공이 멈춘 지점이 같다면, 각 기울이는 방향에 따라 공 하나를 겹치지 않는 곳으로 이동시킵니다.
- 만약 이렇게 빨간색 공과 파란색 공을 이동시킨 후에 두 지점에 대해 이전에 방문한 적이 있다면 해당 경우는 이전에 탐색했기 때문에 제외하고 다음 경우를 살펴보고, 만약 현재 동작이 10번의 동작은 넘었다면 이 때는 -1을 반환합니다.
- 위 경우들에 포함이 되지 않았다면 방문 체크를 진행하고 다음 탐색에 활용하기 위해 Queue에 넣습니다.
- 이렇게 진행하다 빨간색 공은 구멍 위치에, 파란색 공은 구멍이 아닌 위치에 존재하는 경우가 생긴다면 그 때의 동작 수행 횟수를 반환합니다.
- 방문 체크를 진행할 때는, 빨간색 공과 파란색 공이 같이 움직이기 때문에 각 공을 따로 볼 수 없으므로 각 공의 위치를 합쳐 방문 체크를 진행합니다.