[BaekJoon] 1486 등산 (Java)

1.  문제 링크

https://www.acmicpc.net/problem/1486

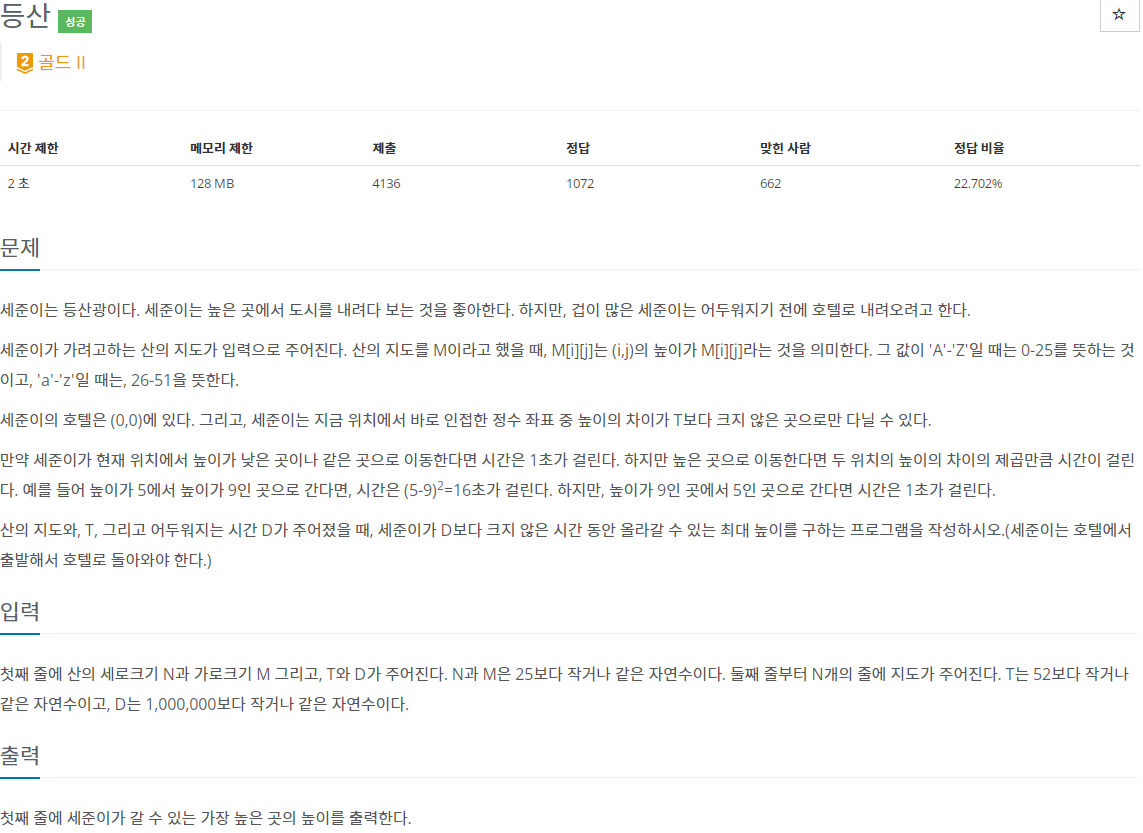
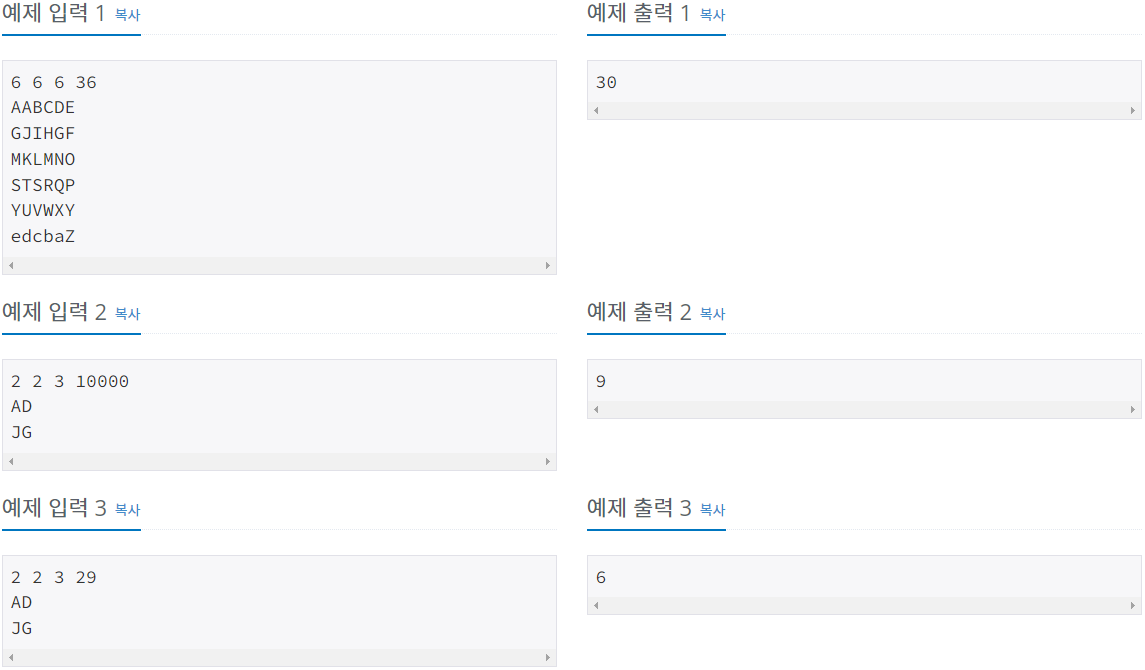
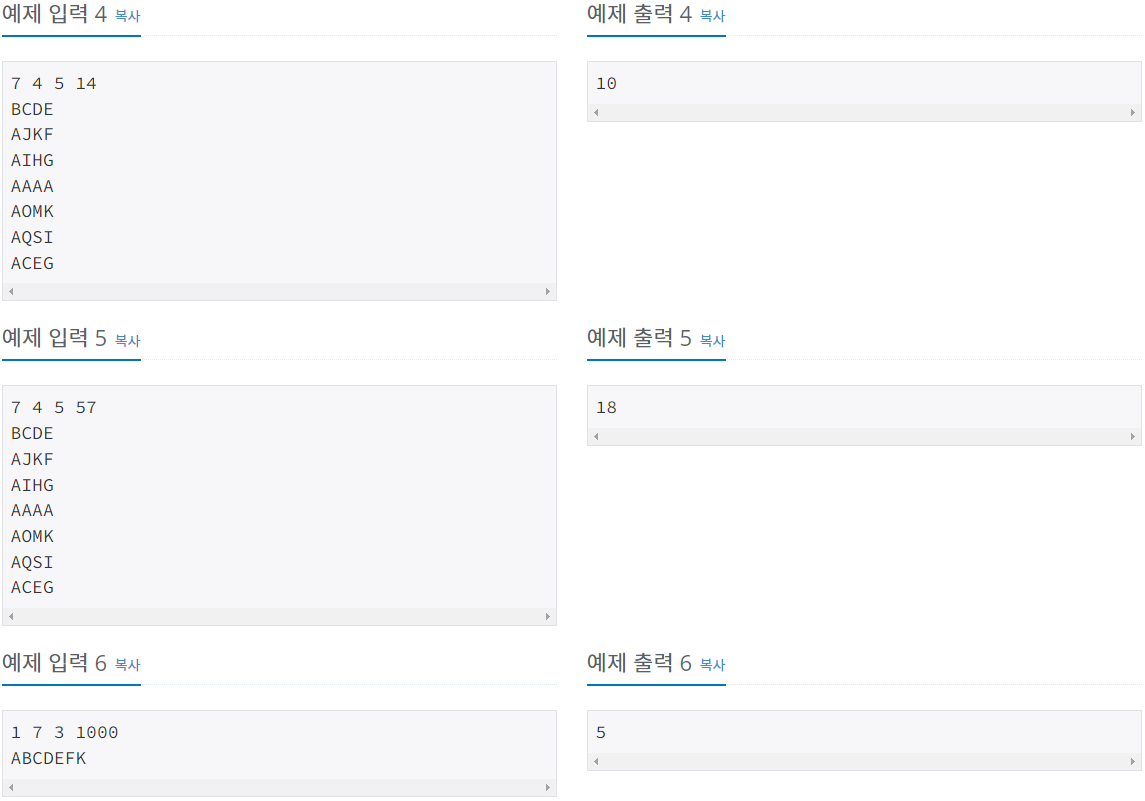
2.  문제

3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class Main {
    static int N, M, T, D;
    static int[][] map; // 산의 지도
    static int[][][][] distance; // 한 위치에서 다른 모든 위치들까지의 최단 시간
    static int[] dx = {-1, 0, 1, 0}, dy = {0, -1, 0, 1};

    static void input() {
        Reader scanner = new Reader();

        N = scanner.nextInt();
        M = scanner.nextInt();
        T = scanner.nextInt();
        D = scanner.nextInt();
        map = new int[N][M];
        distance = new int[N][M][N][M];
        for(int idx = 0; idx < N; idx++) {
            for(int idx2 = 0; idx2 < M; idx2++) {
                for(int idx3 = 0; idx3 < N; idx3++)
                    Arrays.fill(distance[idx][idx2][idx3], Integer.MAX_VALUE);
            }
        }

        for(int row = 0; row < N; row++) {
            String info = scanner.nextLine();
            for(int col = 0; col < M; col++) {
                char curAlphabet = info.charAt(col);

                if(curAlphabet >= 'A' && curAlphabet <= 'Z')
                    map[row][col] = curAlphabet - 'A';
                else if(curAlphabet >= 'a' && curAlphabet <= 'z')
                    map[row][col] = (curAlphabet - 'a') + 26;
            }
        }
    }

    static void solution() {
        // 각 위치에서 모든 위치까지의 최단 시간을 다익스트라 알고리즘을 통해 구한다
        for(int row = 0; row < N; row++) {
            for(int col = 0; col < M; col++)
                dijkstra(row, col);
        }

        // 시작점부터 출발하여 다시 시작점으로 돌아올 수 있는 경로 중 가장 높은 곳의 높이를 가져와 출력한다
        System.out.println(findMax());
    }

    static int findMax() {
        int max = Integer.MIN_VALUE;

        // 시작점부터 시작해서 각 산의 위치까지 시작점부터 갔다가 돌아올 수 있는 위치를 찾고
        // 그 위치들 중에서 가장 높은 곳의 높이를 구한다
        for(int row = 0; row < N; row++) {
            for(int col = 0; col < M; col++) {
                if(distance[row][col][0][0] == Integer.MAX_VALUE ||
                        distance[0][0][row][col] == Integer.MAX_VALUE)
                    continue;

                if(distance[row][col][0][0] + distance[0][0][row][col] <= D)
                    max = Math.max(max, map[row][col]);
            }
        }

        return max;
    }

    static void dijkstra(int x, int y) {
        PriorityQueue<Loc> queue = new PriorityQueue<>();

        distance[x][y][x][y] = 0; // 시작점의 시간은 0
        queue.offer(new Loc(x, y, 0)); // 시작점을 PriorityQueue에 넣고 다익스트라 알고리즘 시작

        while(!queue.isEmpty()) {
            Loc cur = queue.poll();
            // 만약 이미 이전에 구한 최소 시간이 현재 그 위치까지 온 시간보다 작다면
            // 이미 이 경우는 최소 시간이 될 수 없다는 뜻이므로 다음 경우로 넘어간다
            if(distance[cur.x][cur.y][x][y] < cur.time) continue;

            // 인접한 위치들 중 T 이하로 높이 차이가 나는 곳들 중에서
            // 그 위치까지 가는 시간이 D 이하이고 그 위치까지 가는 시간이 이전에 구한 최소 시간보다 작다면
            // 최소 시간을 갱신하고 다음 탐색을 위해 Queue에 넣는다
            for(int dir = 0; dir < 4; dir++) {
                int cx = cur.x + dx[dir], cy = cur.y + dy[dir], nextTime = 0;

                if(isInMap(cx, cy) && Math.abs(map[cur.x][cur.y] - map[cx][cy]) <= T) {
                    if(map[cx][cy] <= map[cur.x][cur.y]) nextTime = cur.time + 1;
                    else nextTime = (int)Math.pow((map[cx][cy] - map[cur.x][cur.y]), 2) + cur.time;

                    if(distance[cx][cy][x][y] > nextTime && nextTime <= D) {
                        distance[cx][cy][x][y] = nextTime;
                        queue.offer(new Loc(cx, cy, nextTime));
                    }
                }
            }
        }
    }

    static boolean isInMap(int x, int y) {
        return x >= 0 && x < N && y >= 0 && y < M;
    }

    static class Loc implements Comparable<Loc> {
        int x, y, time;

        public Loc(int x, int y, int time) {
            this.x = x;
            this.y = y;
            this.time = time;
        }

        @Override
        public int compareTo(Loc o) {
            return time - o.time;
        }
    }

    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;

        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }

        String next() {
            while(st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }

            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }

        String nextLine() {
            String str = "";
            try {
                str = br.readLine();
            } catch (IOException e) {
                e.printStackTrace();
            }

            return str;
        }
    }
}