[BaekJoon] 1507 궁금한 민호 (Java)

1.  문제 링크

https://www.acmicpc.net/problem/1507

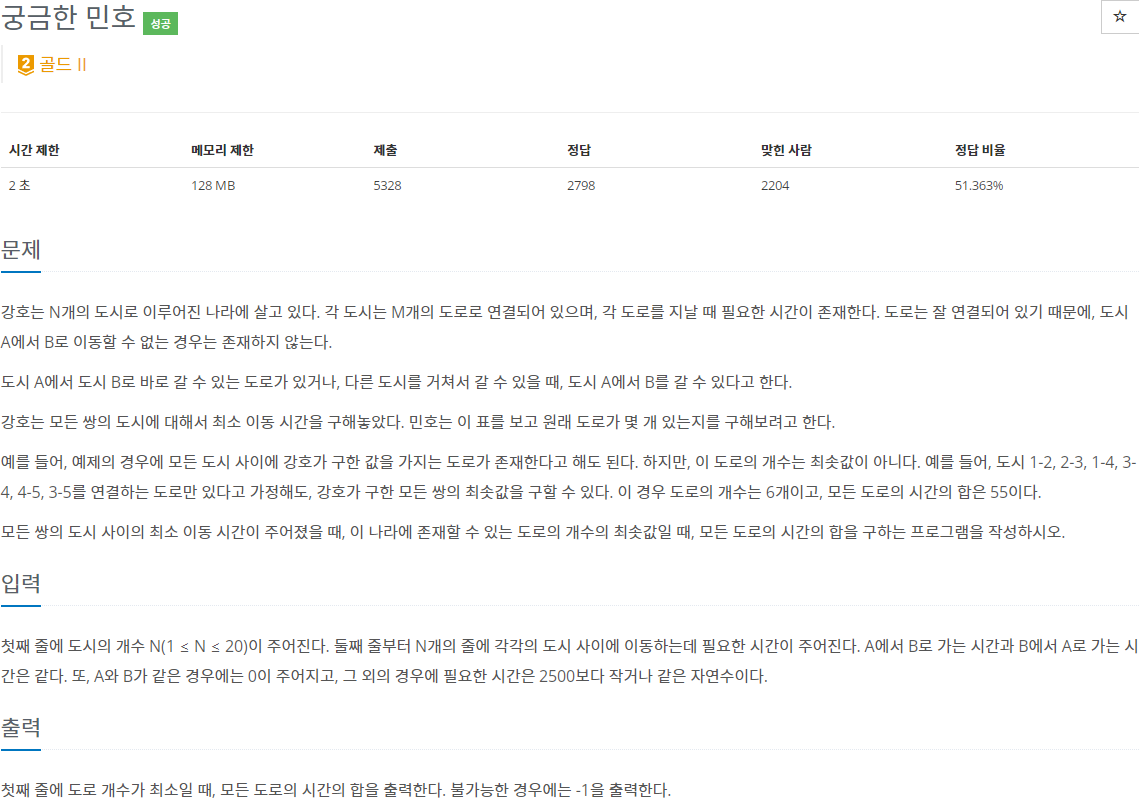
2.  문제

요약

• 강호는 N개의 도시로 이루어진 나라에 살고 있는데, 각 도시는 M개의 도롤 연결되어 있고, 각 도로를 지날 때 필요한 시간이 존재합니다.
• 도로는 잘 연결되어 있으므로, 도시 A에서 도시 B로 이동할 수 없는 경우는 존재하지 않습니다.
• 강호는 모든 쌍의 도시에 대해서 최소 이동 시간을 구해놓았는데, 해당 표를 보고 원래 도로가 몇 개 있는지 구하려고 합니다.
• 모든 쌍의 도시 사이의 최소 이동 시간이 주어졌을 때, 이 나라에 존재할 수 있는 도로의 개수가 최솟값일 때의 모든 도로의 시간의 합을 구하는 문제입니다.
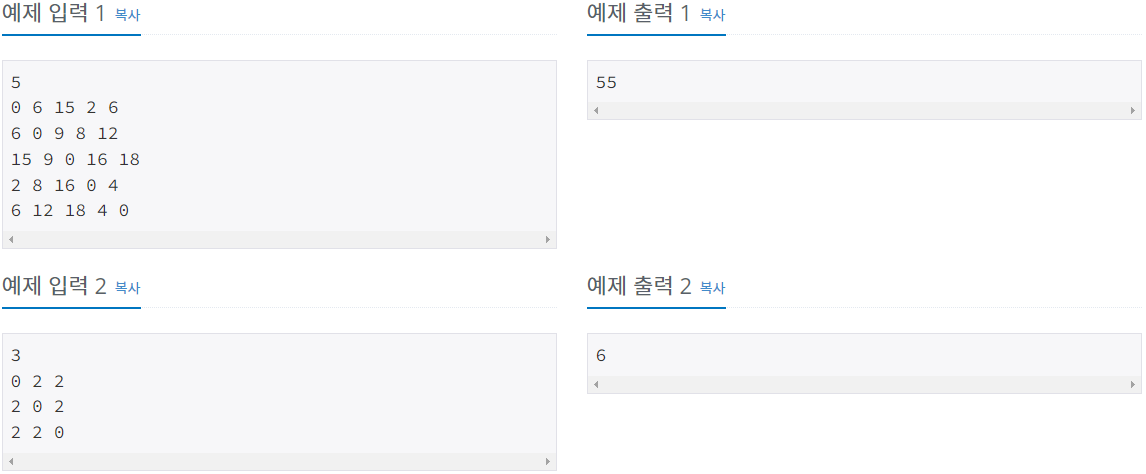
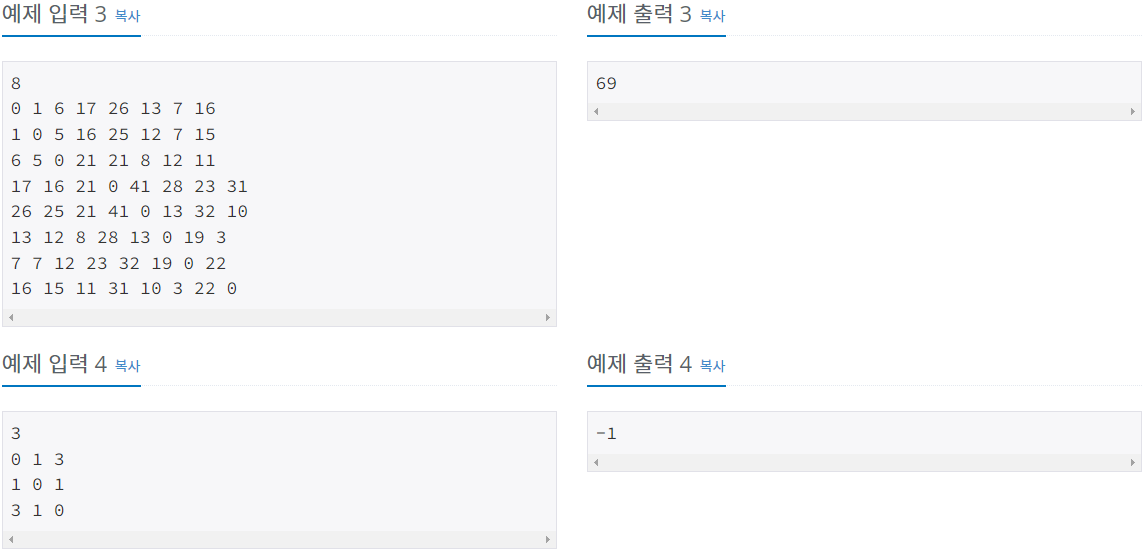
• 입력: 첫 번째 줄에 1보다 크거나 같고 20보다 작거나 같은 도시의 개수 N이 주어지고 두 번째 줄부터 N개의 줄에 각각의 도시 사이에 이동하는데 필요한 시간이 주어집니다. A에서 B로 가는 시간과 B에서 A로 가는 시간은 같고, A와 B가 같은 경우는 0이 주어지며, 그 외의 경우에 필요한 시간인 2500보다 작거나 같은 자연수입니다.
• 출력: 첫 번째 줄에 도로 개수가 최소일 때, 모든 도로의 시간의 합을 출력합니다. 불가능한 경우 -1을 출력합니다.

3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int N;
    static int[][] edges;

    static void input() {
        Reader scanner = new Reader();

        N = scanner.nextInt();
        edges = new int[N][N];

        for(int row = 0; row < N; row++) {
            for(int col = 0; col < N; col++)
                edges[row][col] = scanner.nextInt();
        }
    }

    static void solution() {
        if(!floydWarshall(edges)) {
            System.out.println(-1);
            return;
        }

        System.out.println(getTotalDist(edges));
    }

    static int getTotalDist(int[][] edges) {
        int totalDist = 0;

        for(int row = 0; row < N; row++) {
            for(int col = row + 1; col < N; col++) {
                if(edges[row][col] != Integer.MAX_VALUE)
                    totalDist += edges[row][col];
            }
        }

        return totalDist;
    }

    static boolean floydWarshall(int[][] edges) {
        for(int middle = 0; middle < N; middle++) {
            for(int start = 0; start < N; start++) {
                for(int end = 0; end < N; end++) {
                    if(start == end) continue;
                    if(start == middle) continue;
                    if(middle == end) continue;

                    if(edges[start][middle] == Integer.MAX_VALUE) continue;
                    if(edges[middle][end] == Integer.MAX_VALUE) continue;
                    if(edges[start][end] == Integer.MAX_VALUE) continue;

                    if(edges[start][end] > edges[start][middle] + edges[middle][end]) {
                        return false;
                    }

                    if(edges[start][end] == edges[start][middle] + edges[middle][end]) {
                        edges[start][end] = Integer.MAX_VALUE;
                        edges[end][start] = Integer.MAX_VALUE;
                    }
                }
            }
        }

        return true;
    }


    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;

        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }

        String next() {
            while(st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }

            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }
    }
}

4.  접근

• 주어진 최소 이동 시간 정보들을 edges라는 2차원 배열에 저장해놓고 시작합니다.

• 입력으로 주어진 정보가 모든 도시에 대해 한 도시에서 다른 모든 도시로 이동하는 최소 이동 시간이므로 결국 플로이드-워셜 알고리즘을 통해 구한 최소 이동 시간을 입력으로 받은 것과 같습니다.
• 플로이드-워셜 알고리즘을 생각해보면 시작 지점에서 중간 어느 지점을 거쳐서 도착 지점까지 가는 이동 시간이 시작 지점에서 도착 지점까지 곧장 가는 이동 시간보다 짧다면 값을 갱신해줍니다.
• 그렇다면 최소 이동 시간 배열에 플로이드-워셜 알고리즘을 다시 적용한다면 아래와 같은 조건을 통해 필수적으로 필요하지는 않은 도로를 알 수 있습니다.
  • 시작 지점에서 중간 어느 지점을 거쳐 도착 지점까지 가는 이동 시간이 시작 지점에서 도착 지점까지 곧장 가는 이동 시간과 같다면 중간 지점을 거쳐 가도 최소 이동 시간이 되므로 시작 지점에서 도착 지점으로 곧장 가는 도로는 필요가 없어지게 됩니다.
    • 시작 지점에서 도착 지점으로 곧장 가는 도로는 시작 지점과 도착 지점 두 도시를 오갈때 사용할텐데 다른 도로를 통해 갈 수 있으니 곧장 가는 도로는 사라져도 이동하는데에 문제가 생기지 않습니다.
  • 시작 지점에서 중간 어느 지점을 거쳐 도착 지점까지 가는 이동 시간이 시작 지점에서 도착 지점까지 곧장 가는 이동 시간보다 짧다면 최소 이동 시간을 구하여 입력으로 준 상황인데 다른 도시를 거쳐 더 짧은 시간에 갈 수 있다는 뜻은 최소 이동 시간에 반하는 케이스이므로 모순된 상황이기에 -1을 출력합니다.

static boolean floydWarshall(int[][] edges) {
    for(int middle = 0; middle < N; middle++) {
        for(int start = 0; start < N; start++) {
            for(int end = 0; end < N; end++) {
                if(start == end) continue;
                if(start == middle) continue;
                if(middle == end) continue;

                if(edges[start][middle] == Integer.MAX_VALUE) continue;
                if(edges[middle][end] == Integer.MAX_VALUE) continue;
                if(edges[start][end] == Integer.MAX_VALUE) continue;

                if(edges[start][end] > edges[start][middle] + edges[middle][end]) {
                    return false;
                }

                if(edges[start][end] == edges[start][middle] + edges[middle][end]) {
                    edges[start][end] = Integer.MAX_VALUE;
                    edges[end][start] = Integer.MAX_VALUE;
                }
            }
        }
    }

    return true;
}

• 위 조건들을 이용하여 도로 개수가 최소일 때의 도로들을 구하고 해당 도로들의 시간을 모두 더해줍니다.