1. 문제 링크
https://www.acmicpc.net/problem/1707
2. 문제
요약
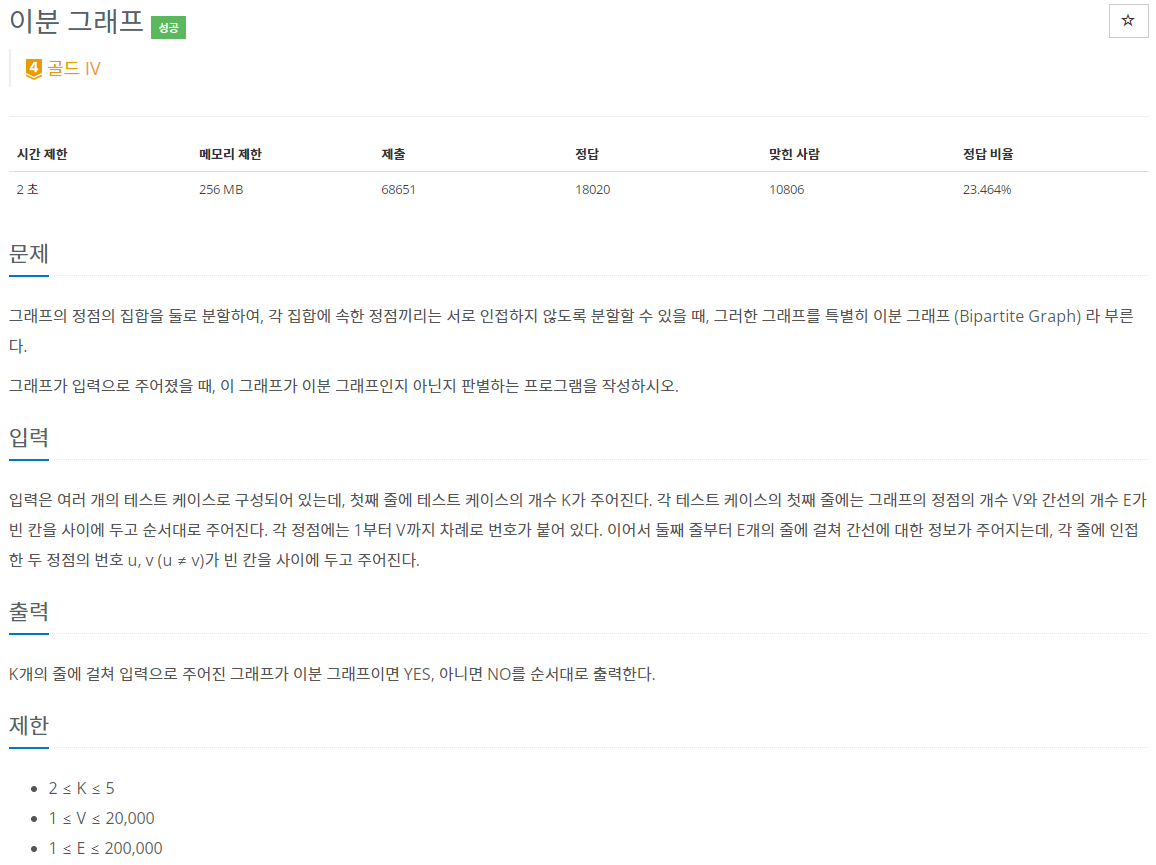
- 그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 이분 그래프(Bipartite Graph)라 부릅니다.
- 그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 판별하는 문제입니다.
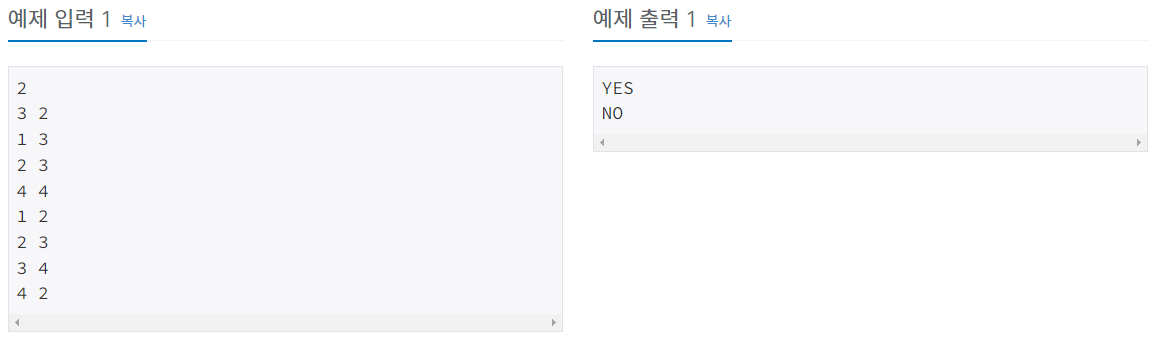
- 입력: 첫 번째 줄에 2보다 크거나 같고 5보다 작거나 같은 테스트 케이스의 개수 K가 주어지고, 각 테스트 케이스의 첫 번째 줄에는 1보다 크거나 같고 20,000보다 작거나 같은 그래프의 정점의 개수 V와 1보다 크거나 같고 200,000보다 작거나 같은 간선의 개수 E가 주어집니다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있습니다. 테스트 케이스의 두 번째 줄부터 E개의 줄에는 간선에 대한 정보가 주어지는데, 각 줄에 u ≠ v인 인접한 두 정점의 번호 u, v가 주어집니다.
- 출력: K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력합니다.
3. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.StringTokenizer;
public class Main {
static StringBuilder sb = new StringBuilder();
static int V, E;
static int[] colors;
static boolean isTree = true;
static HashMap<Integer, ArrayList<Integer>> map;
static void input() {
Reader scanner = new Reader();
int test_num = scanner.nextInt();
for(int i = 0; i < test_num; i++) {
V = scanner.nextInt();
E = scanner.nextInt();
colors = new int[V + 1];
map = new HashMap<>();
isTree = true;
for(int j = 1; j <= V; j++) map.put(j, new ArrayList<Integer>());
for(int j = 0; j < E; j++) {
int u = scanner.nextInt();
int v = scanner.nextInt();
map.get(u).add(v);
map.get(v).add(u);
}
for(int j = 1; j <= V; j++) {
if(!isTree) break;
if(colors[j] == 0) dfs(j, 1);
}
sb.append(isTree ? "YES" : "NO").append('\n');
}
}
static void dfs(int node, int color) {
colors[node] = color;
for(int n : map.get(node)) {
if(colors[n] == color) {
isTree = false;
return;
}
if(colors[n] == 0) dfs(n, -color);
}
}
public static void main(String[] args) {
input();
System.out.println(sb);
}
static class Reader {
BufferedReader br;
StringTokenizer st;
public Reader() {
br = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while(st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
return st.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
}
}4. 접근
이분 그래프
- 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프를 의미합니다.
- 즉, 그래프의 모든 정점이 두 그룹으로 나뉘어지고 서로 다른 그룹의 정점이 간선으로 연결되어 있는 그래프를 말합니다.
- 이분 그래프인지 확인하는 방법은 BFS, DFS 탐색을 이용합니다.
- 모든 정점을 방문하며 간선을 검사하기 때문에 시간 복잡도는 O(V + E)가 됩니다.
구현
- 최초 탐색 시작할 정점의 색상을 정하고 그 색으로 칠합니다.
- 최초 정점의 인접 정점들의 색상을 다른 색으로 칠합니다.
- 인접 정점들을 차례로 탐색하여 자신과 인접한 정점을 다른 색으로 칠합니다.
- 이러한 탐색을 지속하여 2개의 색상으로 모두 칠합니다.
- 색상을 칠하다가 이웃 정점이 같은 색으로 칠해져있다면 이분 그래프가 아닌 것으로 판별합니다.
풀이
- 해당 문제는 BFS, DFS를 이용하여 해결할 수 있는데 저는 DFS를 이용하여 해결해보았습니다.
- 각 테스트 케이스를 입력받고 해당 그래프가 이분 그래프인지 확인한 후에 다음 테스트 케이스를 입력받는 식으로 문제를 해결합니다.
- 그래프를 HashMap 자료구조 변수인 map에 저장합니다. 이 때, 이 그래프는 무방향 그래프이기 때문에 간선의 두 정점 모두에 각 정점을 인접 정점으로 추가합니다.
- 1번 정점부터 V번 정점까지 탐색하며 각 정점에 색을 채워나가고, 이러한 과정에서 이분 그래프인지 확인합니다. 색은 1과 -1로 채울 예정입니다.
- isTree 변수가 이분 그래프인지를 나타내는 변수인데, 탐색하는 과정 중 isTree가 false라면 이미 이분 그래프가 아니라는 것을 확인했기 때문에 다음 정점의 탐색은 하지 않고 NO를 출력해줍니다.
- 각 정점의 색깔을 나타내는 1차원 배열 변수 colors를 각 테스트 케이스마다 생성하고, 현재 탐색하는 정점의 colors 값이 0이라면, 아직 색이 칠해지지 않았다는 뜻이므로 해당 정점을 탐색합니다. 해당 정점은 색깔 1로 칠하고, 인접 정점들의 색을 dfs 함수를 통해 칠합니다.
dfs 함수
static void dfs(int node, int color) {
colors[node] = color;
for(int n : map.get(node)) {
if(colors[n] == color) {
isTree = false;
return;
}
if(colors[n] == 0) dfs(n, -color);
}
}- dfs 함수에 넘겨진 정점을 node, dfs 함수에 넘겨진 색깔을 color라고 한다면 node를 color 색깔로 칠합니다.
- node의 인접 정점들을 탐색하며 인접 정점들의 색을 채워나갑니다.
- 만약 인접 정점의 colors 값이 color와 같다면, 즉 node의 색과 node의 인접 정점의 색이 같다면 이분 그래프가 될 수 없으므로 isTree를 false로 변경하고 다른 인접 정점을 탐색하지 않고 dfs 함수를 끝냅니다.
- 만약 인접 정점의 colors 값이 0이라면, 즉 아직 해당 인접 정점이 색이 칠해지지 않았다면 재귀함수를 호출하여 이 인접 정점에 색을 채워주고 이 인접 정점의 인접 정점들의 색을 칠합니다. 색은 color와 다른 색으로 칠해야하므로 재귀함수를 호출할 때 -color를 넘겨줍니다.