1. 문제 링크
https://www.acmicpc.net/problem/17822
2. 문제
요약
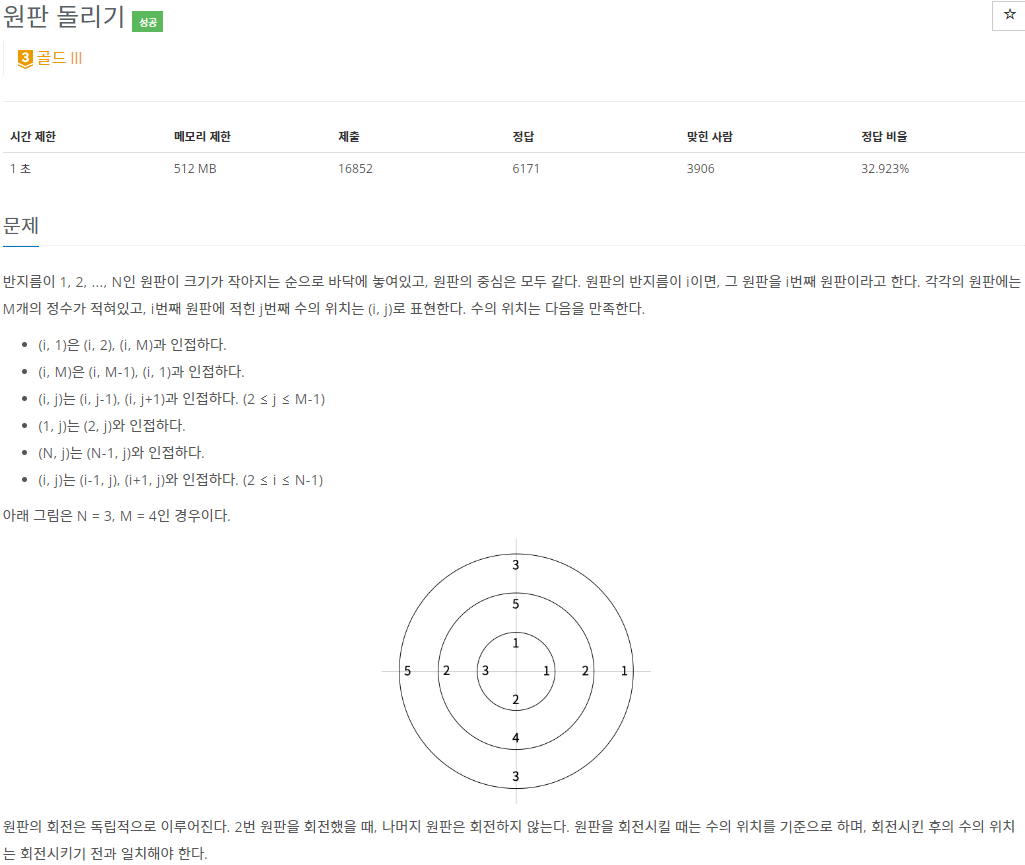
- 반지름이 1, 2, ..., N인 원판이 크기가 작아지는 순으로 바닥에 놓여있고, 원판의 중심은 모두 같습니다.
- 원판의 반지름이 i이면, 그 원판을 i번째 원판이라고 합니다.
- 각 원판에는 M개의 정수가 적혀있고, i번째 원판에 적힌 j번째 수의 위치는 (i, j)로 표현하는데, 수의 위치는 다음을 만족합니다.
- (i, 1)은 (i, 2), (i, M)과 인접합니다.
- (i, M)은 (i, M - 1), (i, 1)과 인접합니다.
- (i, j)는 (i, j - 1), (i, j + 1)과 인접합니다. (2 ≤ j ≤ M-1)
- (i, j)는 (2, j)와 인접합니다.
- (N, j)는 (N - 1, j)와 인접합니다.
- (i, j)는 (i - 1, j), (i + 1, j)와 인접합니다. (2 ≤ i ≤ N-1)
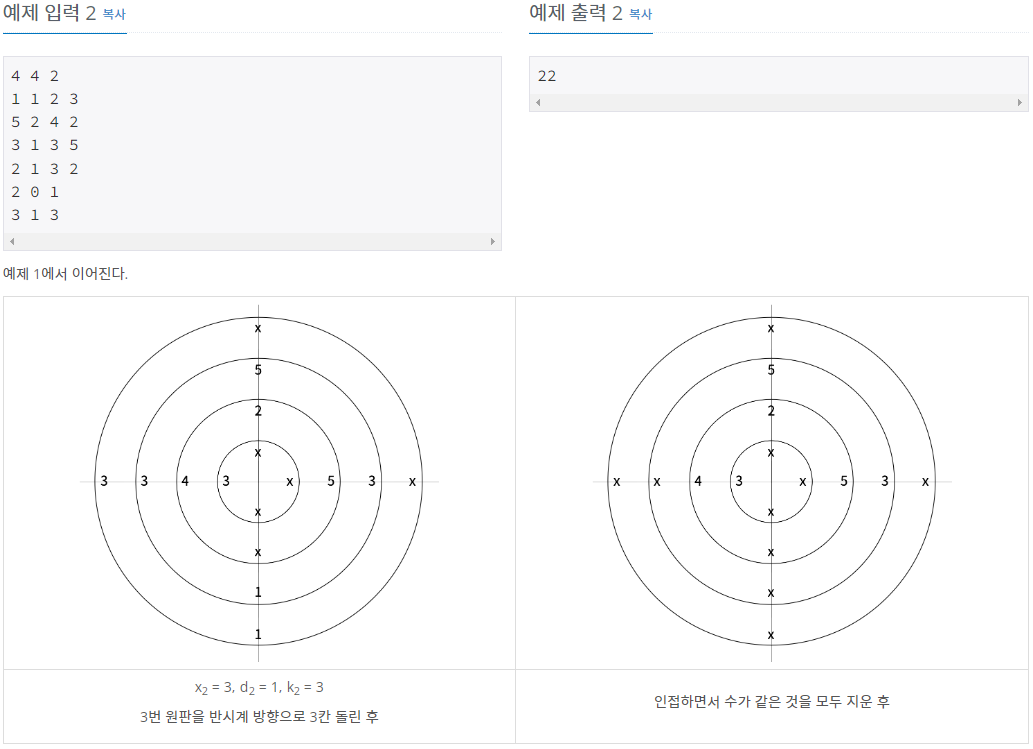
- 원판을 회전시킬 때는 수의 위치를 기준으로 하며, 회전시킨 후의 수의 위치는 회전시키기 전과 일치해야 합니다.
- 이러한 원판의 회전은 원판마다 독립적으로 이루어집니다.
- 원판을 아래와 같은 방법으로 총 T번 회전시키려고 합니다. 원판의 회전 방법은 미리 정해져 있고, i번째 회전할 때 사용하는 변수는 입니다.
- 번호가 의 배수인 원판을 방향으로 칸 회전시킵니다. 가 0인 경우는 시계 방향, 1인 경우는 반시계 방향을 의미합니다.
- 없는 경우에는 원판에 적힌 수의 평균을 구하고, 평균보다 큰 수에서 1을 빼고, 작은 수에는 1을 더합니다.
- 원판을 T번 회전시킨 후 원판에 적힌 수의 합을 구하는 문제입니다.
- 입력: 첫 번째 줄에 2보다 크거나 같고 50보다 작거나 같은 N, M과 1보다 크거나 같고 50보다 작거나 같은 T가 주어지고 두 번째 줄부터 N개의 줄에 원판에 적힌 수가 주어집니다. i번째 줄의 j번째 수는 (i, j)에 적힌 수를 의미합니다. 다음 T개의 줄에 가 주어집니다.
- 출력: 첫 번째 줄에 원판을 T번 회전시킨 후 원판에 적힌 수의 합을 출력합니다.
3. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int N, M, T, platesNumCount;
static int[] xi, di, ki;
static int[][] plates;
static void input() {
Reader scanner = new Reader();
N = scanner.nextInt();
M = scanner.nextInt();
T = scanner.nextInt();
plates = new int[N + 1][M];
for(int plate = 1; plate <= N; plate++) {
for(int num = 0; num < M; num++) plates[plate][num] = scanner.nextInt();
}
platesNumCount = N * M;
xi = new int[T];
di = new int[T];
ki = new int[T];
for(int count = 0; count < T; count++) {
xi[count] = scanner.nextInt();
di[count] = scanner.nextInt();
ki[count] = scanner.nextInt();
}
}
static void solution() {
for(int count = 0; count < T; count++) {
int[] rotatePlates = getRotatePlates(xi[count]);
boolean[][] visited = new boolean[N + 1][M];
rotate(rotatePlates, di[count], ki[count]);
remove();
}
int answer = sumNums();
System.out.println(answer);
}
static int[] getRotatePlates(int n) {
int[] rotatePlates = new int[N / n];
int index = 0;
for(int plate = 1; plate <= N; plate++) {
if(plate % n == 0) {
rotatePlates[index] = plate;
index++;
}
}
return rotatePlates;
}
static int sumNums() {
int answer = 0;
for(int plate = 1; plate <= N; plate++) {
for(int idx = 0; idx < M; idx++) answer += plates[plate][idx];
}
return answer;
}
static void remove() {
boolean isChanged = false;
boolean[][] visited = new boolean[N + 1][M];
for(int plate = 1; plate <= N; plate++) {
boolean c1 = findSameInSamePlate(plate, visited);
boolean c2 = findSameInNeighborPlate(plate, visited);
if(!c1 && !c2) {
continue;
}
isChanged = true;
}
if(isChanged) removeSames(visited);
else changeNums();
}
static void changeNums() {
int sum = sumNums();
double avg = (double)sum / platesNumCount;
adjust(avg);
}
static void adjust(double avg) {
for(int plate = 1; plate <= N; plate++) {
for(int idx = 0; idx < M; idx++) {
if(plates[plate][idx] == 0) continue;
if(plates[plate][idx] > avg) plates[plate][idx]--;
else if(plates[plate][idx] < avg) plates[plate][idx]++;
}
}
}
static void removeSames(boolean[][] visited) {
for(int plate = 1; plate <= N; plate++) {
for(int idx = 0; idx < M; idx++) {
if(visited[plate][idx]) {
plates[plate][idx] = 0;
platesNumCount--;
}
}
}
}
static boolean findSameInSamePlate(int plate, boolean[][] visited) {
boolean isChanged = false;
for(int idx = 0; idx < M; idx++) {
if(plates[plate][idx] == 0) continue;
int left = idx - 1, right = idx + 1;
if(left == -1) left = M - 1;
if(right == M) right = 0;
if(plates[plate][idx] == plates[plate][left]) {
visited[plate][idx] = true;
visited[plate][left] = true;
isChanged = true;
}
if(plates[plate][idx] == plates[plate][right]) {
visited[plate][idx] = true;
visited[plate][right] = true;
isChanged = true;
}
}
return isChanged;
}
static boolean findSameInNeighborPlate(int plate, boolean[][] visited) {
boolean isChanged = false;
for(int idx = 0; idx < M; idx++) {
if(plates[plate][idx] == 0) continue;
int prev = plate - 1, next = plate + 1;
if(prev != 0) {
if(plates[plate][idx] == plates[prev][idx]) {
visited[plate][idx] = true;
visited[prev][idx] = true;
isChanged = true;
}
}
if(next != N + 1) {
if(plates[plate][idx] == plates[next][idx]) {
visited[plate][idx] = true;
visited[next][idx] = true;
isChanged = true;
}
}
}
return isChanged;
}
static void rotate(int[] rotatePlates, int direction, int amount) {
for(int plate : rotatePlates)
rotatePlate(plate, direction, amount);
}
static void rotatePlate(int plate, int direction, int amount) {
int dir = direction == 0 ? 1 : -1;
int[] newNum = new int[M];
for(int idx = 0; idx < M; idx++) {
int newIdx = idx + (dir * amount);
if(Math.abs(newIdx) >= M) {
if(newIdx < 0) {
newIdx %= M;
newIdx = M - newIdx;
} else {
newIdx %= M;
}
} else {
if(newIdx < 0) newIdx = M + newIdx;
}
newNum[newIdx] = plates[plate][idx];
}
plates[plate] = newNum.clone();
}
public static void main(String[] args) {
input();
solution();
}
static class Reader {
BufferedReader br;
StringTokenizer st;
public Reader() {
br = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while(st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return st.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
}
}4. 접근
- 주어진 T개의 () 값을 이용하여 T번 원판을 회전하는데, 각 회전마다 아래와 같은 작업을 거칩니다.
- 우선 의 배수인 원판들, 즉 회전시켜야하는 원판들을 getRotatePlates 함수를 통해 구합니다.
- 1번 원판부터 N번 원판까지 로 나눠보고 나누어떨어지는 원판들은 rotatePlates라는 1차원 배열에 넣습니다.
- rotate 메서드를 통해 위에서 구한 회전시켜야하는 원판들을 회전시킵니다.
- 원판에 있는 각 수의 위치를 조정하는데, 이 때 시계 방향으로 회전시키면 수의 위치를 나타내는 index가 커지는 방향으로 움직이고, 반시계 방향으로 회전시키면 index가 작아지는 방향으로 움직이기 때문에 움직이는 방향을 나타내는 변수 dir의 값을 시계 방향일 때는 1, 반시계 방향일 때는 -1로 설정합니다.
- newNum이라는 1차원 배열을 만들고 원판에 있는 모든 수를 새롭게 재배치하여 newNum에 저장합니다. 재배치는 에 dir을 곱한 값을 원래 index에 더하여 그 위치에 해당 수를 배치합니다.
- 이 때, 구한 index가 음수라면 전체 수의 개수 M에 구한 index를 더하여 해당 수의 위치를 찾아주고, 구한 index의 절댓값이 최대 index인 M - 1보다 크다면 한 바퀴 이상 돌았다는 뜻이므로 그에 맞게 음수일 때와 양수일 때로 나누어 맞는 index를 구해줍니다.
- 이렇게 newNum에 재배치가 됐다면 원래 원판의 수가 적인 배열에 newNum의 값들을 복사해줍니다.
- 인접한 원판들과 혹은 같은 원판에 인접한 수들을 서로 비교하여 인접한 수들 사이에 같은 수들이 있는지 확인하고 그렇다면 해당 수들을 지우는 작업을, 같은 수가 없다면 평균을 구하여 평균보다 큰 수는 1을 빼고 작은 수는 1을 더하는 작업을 진행합니다.
- 인접한 원판들 사이에 같은 위치에 있는 수들에서 같은 수가 있는지 findSameInNeighborPlate 메서드를 통해 찾고 같은 원판에 인접한 수들 사이에 같은 수가 있는지 findSameInSamePlate 메서드를 통해 찾습니다.
- 두 메서드에서는 인접한 위치들에서 같은 수가 있는지 찾고 있다면 2차원 배열 visited에서 해당 위치들의 값을 true로 변경하여 이후에 지워야할 수들이라는 것을 표시합니다.
- 또한 두 메서드에 각각 isChanged라는 변수를 두어 각 메서드에서 같은 수가 있었는지를 나타내줍니다. 이 값을 두 메서드에서 각각 반환하여 이후에 평균을 구해 수를 조정해야하는지 여부를 판단합니다.
- 모든 원판에 대해서 findSameInNeighborPlate 메서드와 findSameInSamePlate 메서드를 수행하였는데 만약 어떠한 한 메서드에서라도 true를 반환했다면 visited에 표시한 값들을 지우고 작업을 끝냅니다.
- 만약 모든 메서드에서 false를 반환했다면 수들의 평균을 구하여 평균보다 작은 수에는 1을 더하는 작업을, 평균보다 큰 수에는 1을 빼는 작업을 진행한 후 작업을 끝냅니다.
- 우선 의 배수인 원판들, 즉 회전시켜야하는 원판들을 getRotatePlates 함수를 통해 구합니다.