[BaekJoon] 2056 작업 (Java)

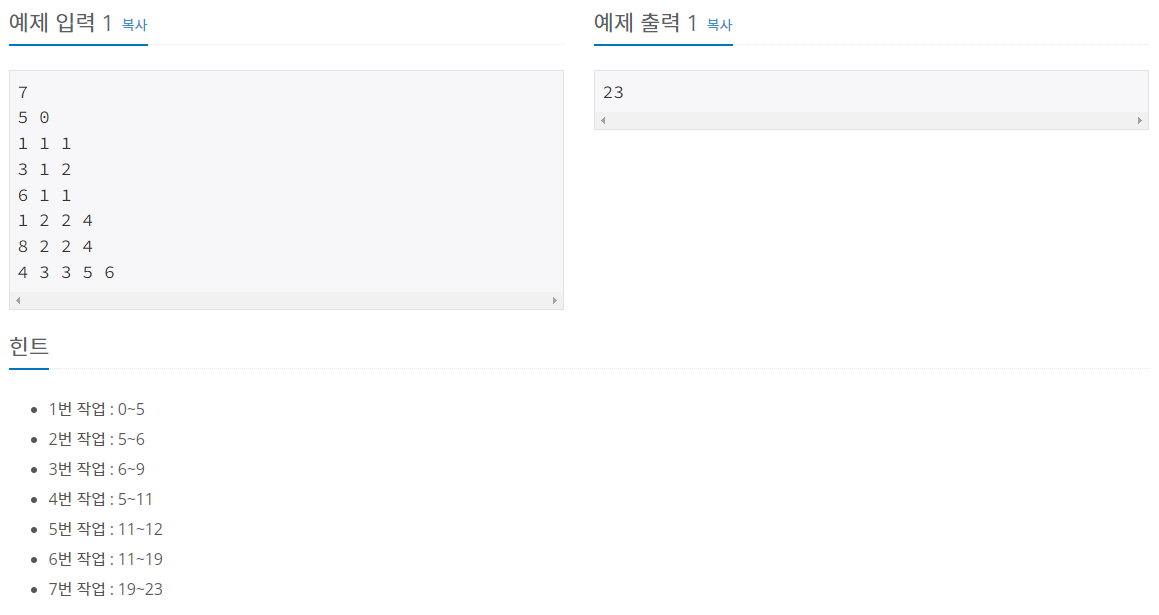
1.  문제 링크

https://www.acmicpc.net/problem/2056

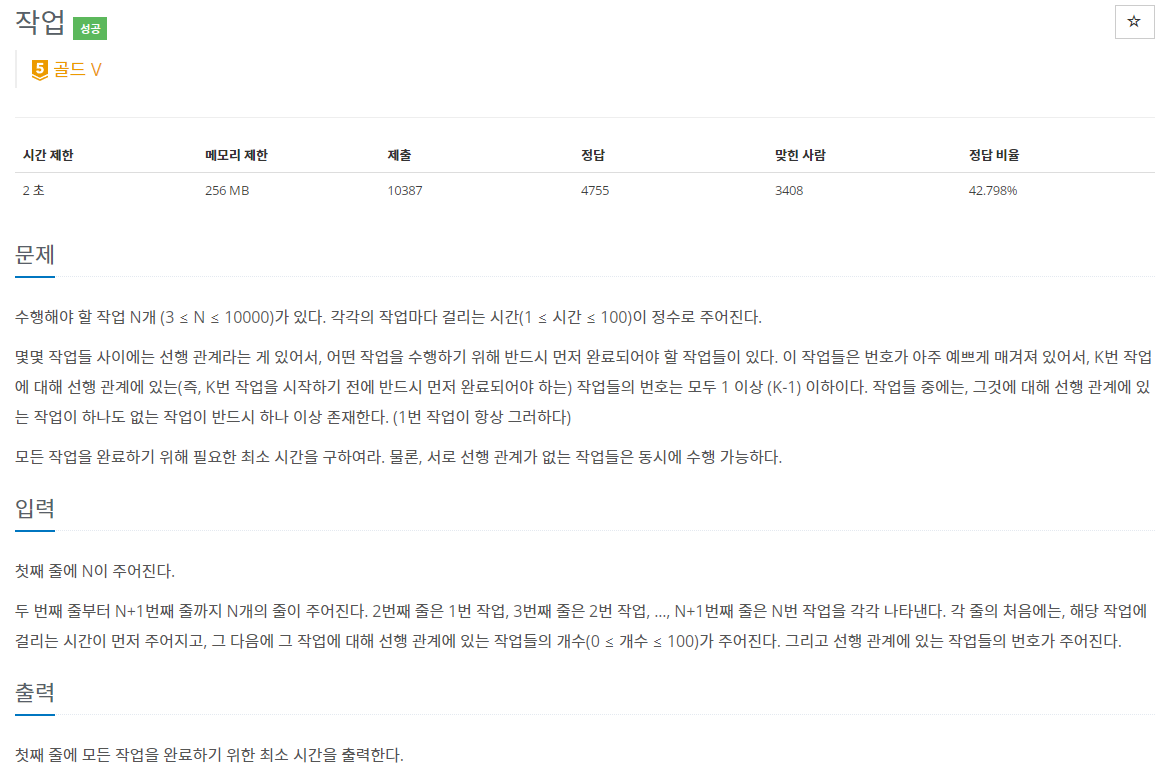
2.  문제

요약

• 수행해야 할 작업 N개가 있고 각각의 작업마다 걸리는 시간이 정수로 주어집니다.
• 몇몇 작업들 사이에는 선행 관계가 있어, 어떤 작업을 수행하기 위해 반드시 먼저 완료되어야 할 작업들이 있습니다.
• K번 작업에 대해 선행 관계에 있는 작업들의 번호는 모두 1 이상 (K - 1) 이하입니다.
• 선행 관계에 있는 작업이 하나도 없는 작업이 반드시 하나 이상 존재합니다.
• 서로 선행 관계가 없는 작업들은 동시에 수행 가능합니다.
• 모든 작업을 완료하기 위해 필요한 시간을 구하는 문제입니다.
• 입력: 첫 번째 줄에 3보다 크거나 같고 10000보다 작거나 같은 N이 주어지고 두 번째 줄부터 N개의 줄에는 각 작업을 나타냅니다.
  • 각 줄의 처음에는 해당 작업에 걸리는 시간이 먼저 주어지고, 그 다음에 0보다 크거나 같고 100보다 작거나 같은 그 작업에 대해 선행 관계에 있는 작업들의 개수가 주어지며 그 다음에 선행 관계에 있는 작업들의 번호가 주어집니다.
• 출력: 첫 번째 줄에 모든 작업을 완료하기 위한 최소 시간을 출력합니다.

3.  소스코드

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Queue;

public class Main {
	public int getMinTime(HashMap<Integer, ArrayList<Integer>> map, int[] time, int[] related_num) {
		Queue<Integer> queue = new LinkedList<Integer>();
		int[] each_time = new int[time.length];
		for(int i = 1; i <= map.size(); i++) {
			each_time[i] = time[i];
			if(related_num[i] == 0) {
				queue.offer(i);
			}
		}
		while(!queue.isEmpty()) {
			int cur_task = queue.poll();
			for(int i : map.get(cur_task)) {
				related_num[i]--;
				each_time[i] = Math.max(each_time[i], each_time[cur_task] + time[i]);
				if(related_num[i] == 0) {
					queue.offer(i);
				}
			}
		}
		int max = 0;
		for(int i = 0; i < each_time.length; i++) {
			max = Math.max(max, each_time[i]);
		}
		return max;
 	}
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		int num = Integer.parseInt(br.readLine());
		HashMap<Integer, ArrayList<Integer>> map = new HashMap<>();
		int[] time = new int[num + 1];
		int[] related_num = new int[num + 1];
		for(int i = 1; i <= num; i++) {
			map.put(i, new ArrayList<Integer>());
		}
		for(int i = 1; i <= num; i++) {
			String[] input = br.readLine().split(" ");
			time[i] = Integer.parseInt(input[0]);
			int n = Integer.parseInt(input[1]);
            related_num[i] = n;
			for(int j = 0; j < n; j++) {
				map.get(Integer.parseInt(input[j + 2])).add(i);
			}
		}
		br.close();
		Main m = new Main();
		bw.write(m.getMinTime(map, time, related_num) + "\n");
		bw.flush();
		bw.close();
	}
}

4.  접근

• 해당 문제는 위상정렬을 적용하여 해결할 수 있는 문제입니다.
• 1번 작업부터 N번 작업까지 주어진 정보들을 이용하여 그래프를 생성하고 각 작업에 대해 선행 관계에 있는 작업들의 개수를 1차원 배열 related_num에 설정합니다.
• 그래프를 생성할 때는 선행 관계가 되는 작업이 해당 작업을 선행 관계 작업으로 갖는 작업들을 ArrayList로 갖고 있기 때문에 방향성이 있는 방향그래프가 됩니다.
• 각 작업에 대해 작업을 수행하는 데에 걸리는 시간을 나타내는 1차원 배열 each_time을 생성하고 주어진 각 작업에 대해 걸리는 시간들을 each_time 배열에 설정합니다.
• 선행 관계에 있는 작업이 없는 작업부터 시작할 것이므로 해당 작업들을 Queue에 넣어줍니다.
• Queue에서 작업들을 하나씩 뺀 후에 해당 작업을 마치며 해당 작업을 선행 작업으로 하는 작업들을 모두 확인하여 각 작업들의 related_num 값을 하나 줄이고 만약 related_num 값이 0이라면 더이상 선행 관계에 있는 작업이 없다는 뜻이므로 해당 작업을 Queue에 넣습니다.
• 이 때, 각 작업들에서의 걸리는 시간은 현재 각 작업에서의 each_time 값과 Queue에서 꺼낸 작업에서의 each_time 값에 현재 각 작업의 걸리는 시간을 더한 값을 비교하여 더 큰 값을 각 작업들에서 걸리는 시간으로 합니다.
  • each_time[i] = Math.max(each_time[i], each_time[cur_task] + time[i])
    • cur_task는 Queue에서 꺼낸 작업을 의미하고, i는 Queue에서 꺼낸 작업을 선행 관계에 있는 작업으로 갖는 작업을 의미합니다.
• 이렇게 각 작업을 완료하는 데에 걸리는 시간을 구하고 각 시간 중 가장 긴 시간이 모든 작업을 완료하기 위한 최소 시간이 됩니다.