[BaekJoon] 2268 수들의 합 7 (Java)

1.  문제 링크

https://www.acmicpc.net/problem/2268

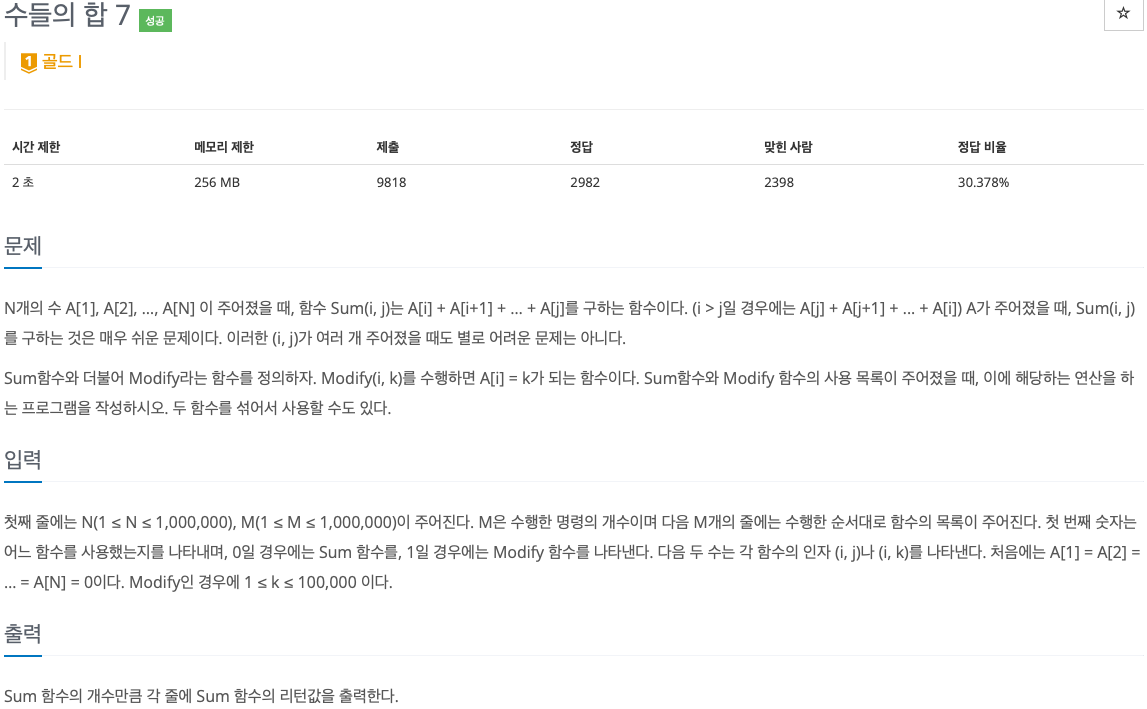
2.  문제

3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int N, M;
    static int[][] orders;

    static void input() {
        Reader scanner = new Reader();

        N = scanner.nextInt();
        M = scanner.nextInt();


        orders = new int[M][3];
        for(int idx = 0; idx < M; idx++) {
            int type = scanner.nextInt(), num1 = scanner.nextInt(), num2 = scanner.nextInt();

            orders[idx][0] = type;
            if(orders[idx][0] == 0) {
                orders[idx][1] = Math.min(num1 - 1, num2 - 1);
                orders[idx][2] = Math.max(num1 - 1, num2 - 1);
            } else {
                orders[idx][1] = num1 - 1;
                orders[idx][2] = num2;
            }
        }
    }

    static void solution() {
        StringBuilder sb = new StringBuilder();
        // 세그먼트의 트리 높이 구하기
        int height = getTreeHeight(N, 2);
        // 세그먼트 트리의 총 노드 개수 구하기
        int nodeCnt = Math.toIntExact(getNodeCnt(height));
        // 리프노드의 시작 인덱스 구하기
        int startIdx = (int)Math.pow(2, height - 1);
        // 세그먼트 트리
        long[] segmentTree = new long[nodeCnt];

        for(int idx = 0; idx < M; idx++) {
            // Sum 함수라면 시작 인덱스부터 끝 인덱스까지의 합 구하기
            if(orders[idx][0] == 0)
                sb.append(getSum(orders[idx][1] + startIdx, orders[idx][2] + startIdx, segmentTree)).append('\n');
            // Modify 함수라면 해당 인덱스의 값을 변경 후, 세그먼트 트리 업데이트하기
            else if(orders[idx][0] == 1)
                modifyNum(orders[idx][1] + startIdx, orders[idx][2], segmentTree);
        }

        System.out.print(sb);
    }

    static long getSum(int startIdx, int endIdx, long[] segmentTree) {
        long sum = 0L;

        // 시작 인덱스가 끝 인덱스보다 작거나 같을 때까지 다음 작업을 진행
        while(startIdx <= endIdx) {
            // 시작 인덱스의 인덱스가 홀수면 묶은 두 개의 노드에서 오른쪽에 있다는 의미
            // 이 때에는 두 개의 노드를 더한 부모 노드 값이 아니라 자기 자신의 값만 더해준다
            if(startIdx % 2 == 1) sum += segmentTree[startIdx];
            // 끝 인덱스의 인덱스가 짝수면 묶은 두 개의 노드에서 왼쪽에 있다는 의미
            // 이 때에는 두 개의 노드를 더한 부모 노드 값이 아니라 자기 자신의 값만 더해준다
            if(endIdx % 2 == 0) sum += segmentTree[endIdx];

            // 만약 시작 인덱스가 홀수면 자기 자신 값은 이미 더해줬기 때문에 다음 두 노드의 부모 노드값을 더해줘야 함
            // 그러므로 시작 인덱스에 1을 더해준 후에 2로 나눠 부모 노드로 이동한다
            startIdx = (startIdx + 1) / 2;
            // 만약 끝 인덱스가 짝수면 자기 자신 값은 이미 더해줬기 때문에 이전 두 노드의 부모 노드값을 더해줘야 함
            // 그러므로 끝 인덱스에 1을 빼준 후에 2로 나눠 부모 노드로 이동한다
            endIdx = (endIdx - 1) / 2;
        }

        return sum;
    }

    static void modifyNum(int targetIdx, int modifiedNum, long[] segmentTree) {
        long gap = modifiedNum - segmentTree[targetIdx]; // 바꾸려는 값과 현재 값의 차이를 구함

        // 부모 노드로 타고 올라가면서 차이를 더해줘 세그먼트 트리를 업데이트
        while(targetIdx > 0) {
            segmentTree[targetIdx] += gap;
            targetIdx /= 2;
        }
    }

    static int getTreeHeight(int size, int base) {
        // log2(수의 개수) -> 이진 트리의 높이
        // 0번 인덱스는 사용하지 않으므로 1을 더해줌
        return (int)Math.ceil(Math.log(size) / Math.log(base)) + 1;
    }

    static long getNodeCnt(int treeHeight) {
        // 높이를 알고 있으니 그것을 이용하여 노드 전체 개수 구함
        return Math.round(Math.pow(2, treeHeight));
    }

    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;

        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }

        String next() {
            while(st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }

            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }
    }
}