1. 문제 링크
https://www.acmicpc.net/problem/28297
2. 문제
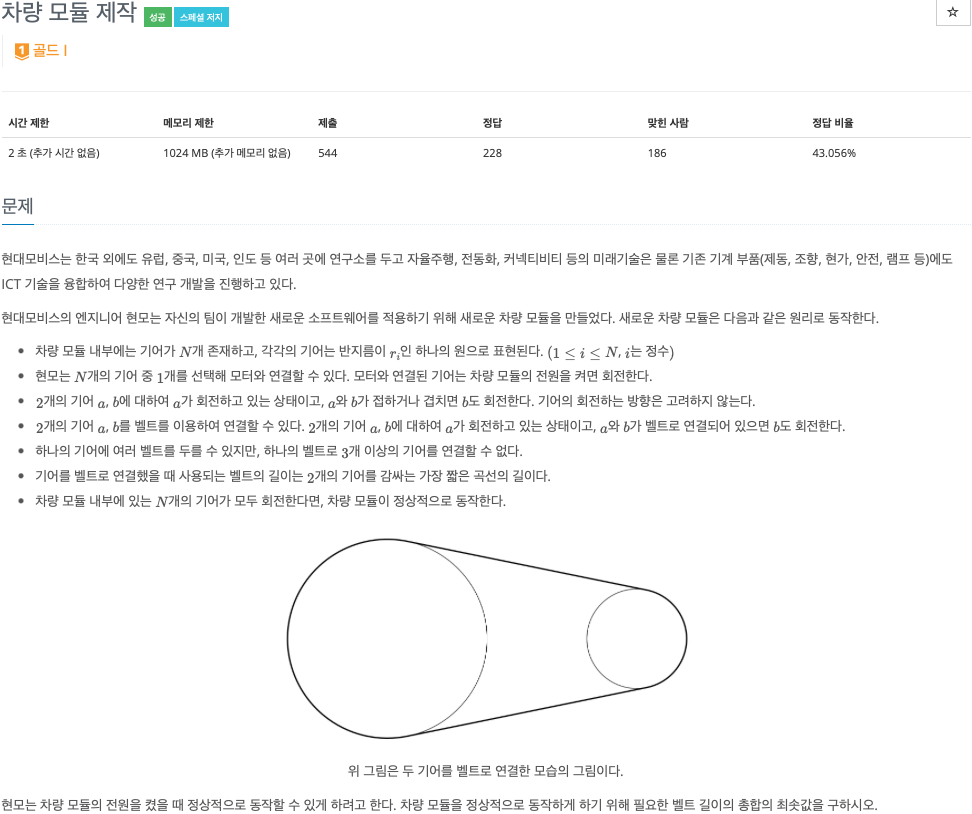

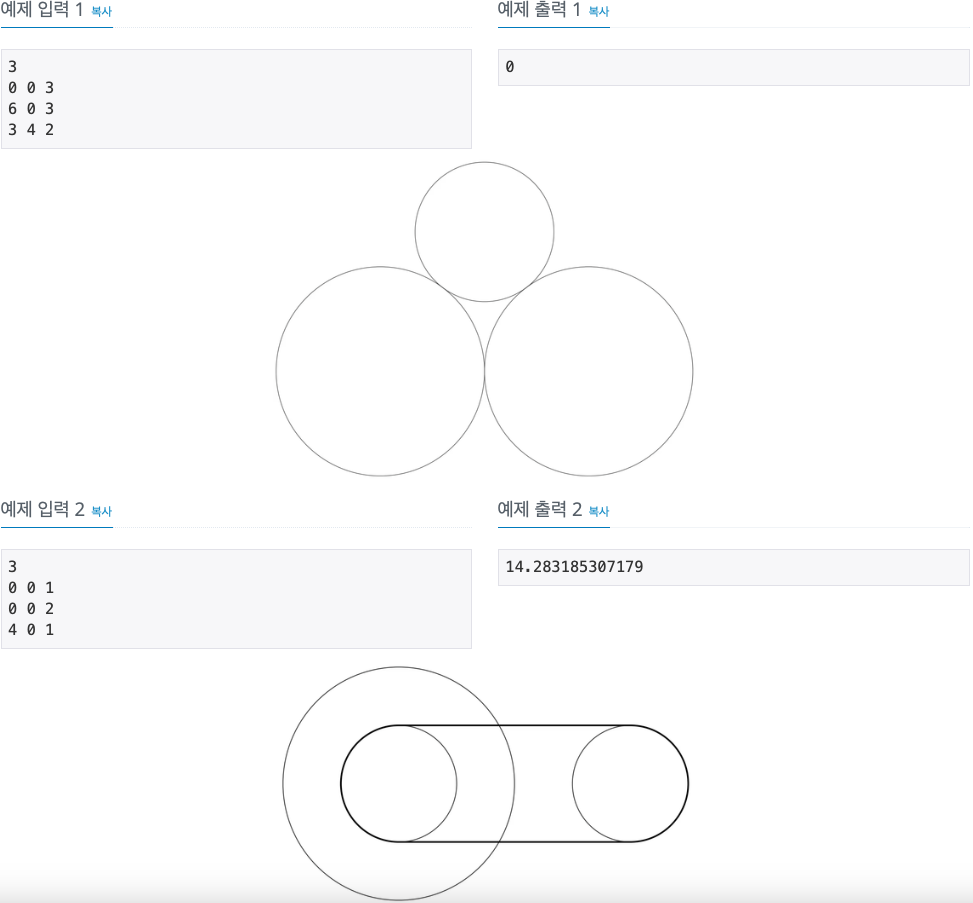
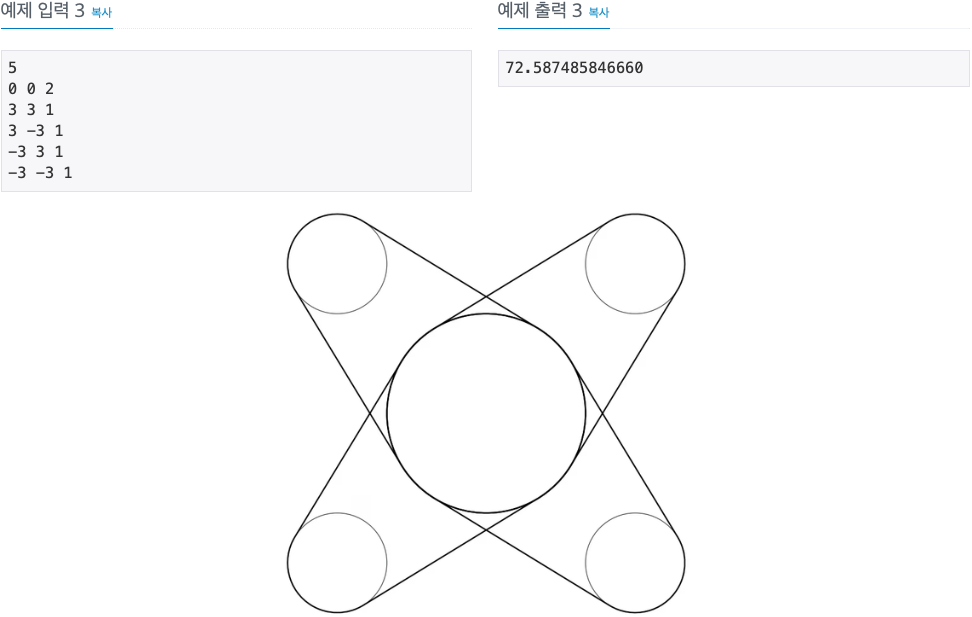
3. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int gearCount;
static int[] parents;
static List<Gear> gears;
static Queue<Belt> belts;
static void input() {
Reader scanner = new Reader();
gearCount = scanner.nextInt();
gears = new ArrayList<>();
parents = new int[gearCount];
for (int gear = 0; gear < gearCount; gear++) {
parents[gear] = gear;
gears.add(new Gear(scanner.nextInt(), scanner.nextInt(), scanner.nextInt()));
}
}
static void solution() {
makeAllBelts();
System.out.println(calculateMinTotalBeltLength());
}
static double calculateMinTotalBeltLength() {
double totalBeltLength = 0;
int count = 0;
while (!belts.isEmpty()) {
Belt belt = belts.poll();
if (!isSameParents(belt.gear1, belt.gear2)) {
union(belt.gear1, belt.gear2);
totalBeltLength += belt.beltLength;
count++;
}
if (count >= gearCount - 1) {
break;
}
}
return totalBeltLength;
}
static int findParent(int gear) {
if (gear == parents[gear]) {
return gear;
}
return parents[gear] = findParent(parents[gear]);
}
static void union(int gear1, int gear2) {
int parent1 = findParent(gear1);
int parent2 = findParent(gear2);
if (parent1 != parent2) {
if (parent1 < parent2) {
parents[parent2] = parent1;
} else {
parents[parent1] = parent2;
}
}
}
static boolean isSameParents(int gear1, int gear2) {
return findParent(gear1) == findParent(gear2);
}
static void makeAllBelts() {
belts = new PriorityQueue<>();
for (int firstGearIdx = 0; firstGearIdx < gearCount; firstGearIdx++) {
for (int secondGearIdx = firstGearIdx + 1; secondGearIdx < gearCount; secondGearIdx++) {
double beltLength = calculateBeltLength(gears.get(firstGearIdx), gears.get(secondGearIdx));
belts.offer(new Belt(firstGearIdx, secondGearIdx, beltLength));
}
}
}
static double calculateBeltLength(Gear gear1, Gear gear2) {
double totalBeltLength = 0;
int maxRadius = Math.max(gear1.radius, gear2.radius);
int minRadius = Math.min(gear1.radius, gear2.radius);
int bottomLineLength = maxRadius - minRadius;
double hypotenuseLength = Math.pow(gear1.x - gear2.x, 2) + Math.pow(gear1.y - gear2.y, 2);
if (minRadius + maxRadius < Math.sqrt(hypotenuseLength)) {
double length = Math.sqrt(hypotenuseLength - Math.pow(bottomLineLength, 2));
totalBeltLength += length * 2;
double theta = Math.acos(bottomLineLength / Math.sqrt(hypotenuseLength));
totalBeltLength += maxRadius * (Math.PI * 2 - 2 * theta);
totalBeltLength += minRadius * (2 * theta);
return totalBeltLength;
}
return 0;
}
static class Gear {
int x;
int y;
int radius;
public Gear(int x, int y, int radius) {
this.x = x;
this.y = y;
this.radius = radius;
}
}
static class Belt implements Comparable<Belt> {
int gear1;
int gear2;
double beltLength;
public Belt(int gear1, int gear2, double beltLength) {
this.gear1 = gear1;
this.gear2 = gear2;
this.beltLength = beltLength;
}
@Override
public int compareTo(Belt o) {
if (beltLength < o.beltLength) {
return -1;
}
if (beltLength > o.beltLength) {
return 1;
}
return 0;
}
}
public static void main(String[] args) {
input();
solution();
}
static class Reader {
BufferedReader br;
StringTokenizer st;
public Reader() {
br = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while (st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return st.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
}
}4. 풀이
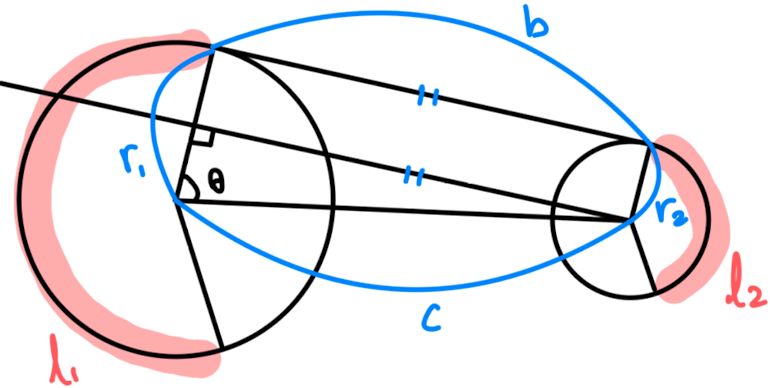
- 위 그림을 기반으로 서로 다른 두 기어를 벨트로 연결하는 데에 필요한 벨트 길이는 이다.
- 와 같은 원주는 아래와 같이 구할 수 있다
- 그러므로 는 각각 다음과 같다.
- 과 의 값은 알 수 있지만 의 값을 알아야만 원주의 길이를 구할 수 있다. 는 다음과 같이 구할 수 있다.
- 를 포함하고 있는 직각 삼각형을 봤을 때, 아래와 같은 식을 만족한다.
- 위와 같은 식이 만족하기 때문에 아래와 같은 식 또한 만족한다.
- 를 포함하고 있는 직각 삼각형을 봤을 때, 아래와 같은 식을 만족한다.
- 위와 같은 과정을 통해 주어진 모든 기어에 대해 서로 다른 두 기어를 벨트로 연결하는 데에 필요한 벨트 길이를 구할 수 있다.
- 이 벨트 정보를 이용하여 MST를 만들면 문제의 답을 구할 수 있다.

