1. 문제 링크
https://www.acmicpc.net/problem/4386
2. 문제
요약
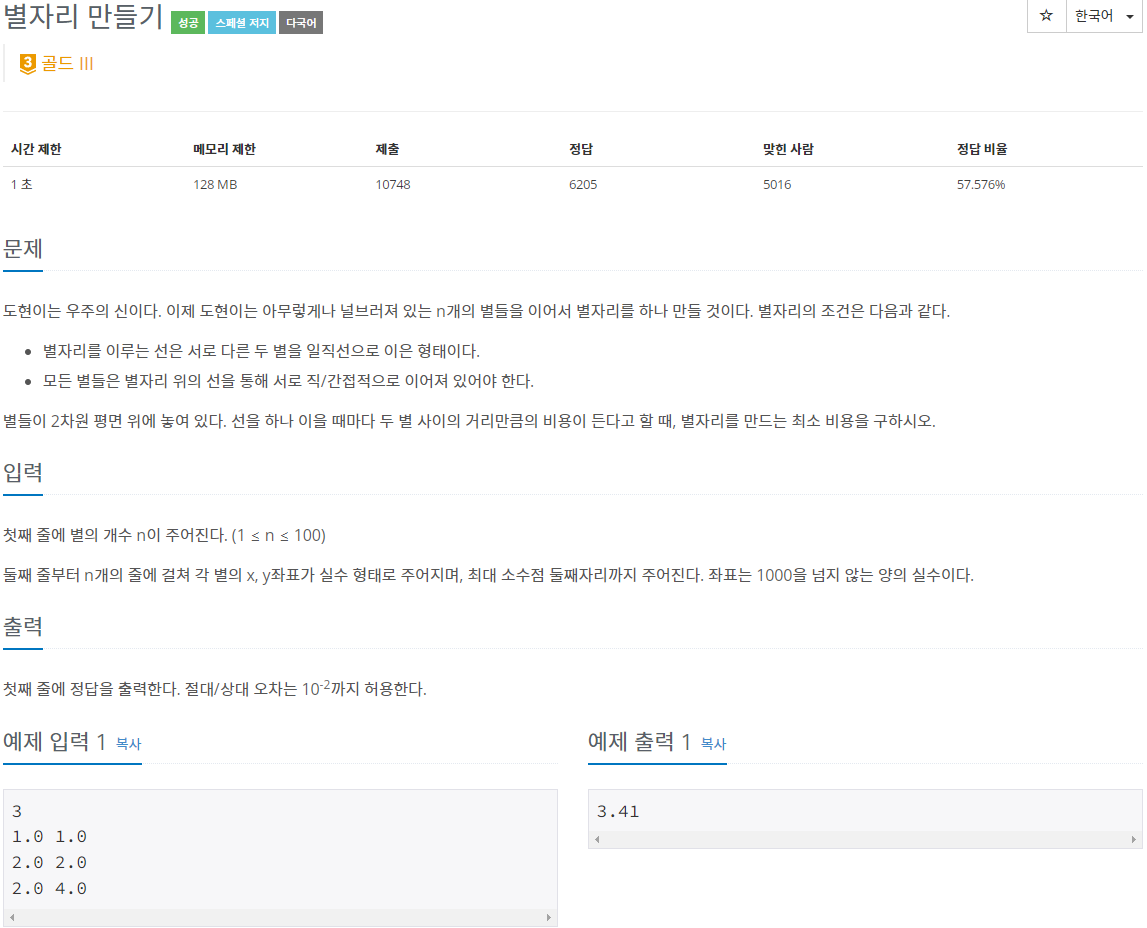
- 도현이는 아무렇게나 널브러져 있는 n개의 별들을 이어서 별자리를 하나 만드려고 하는데, 별자리의 조건은 아래와 같습니다.
- 별자리를 이루는 선은 서로 다른 두 별을 일적선으로 이은 형태입니다.
- 모든 별들은 별자리 위의 선을 통해 서로 직/간접적으로 이어져 있어야 합니다.
- 별들이 2차원 평면 위에 놓여 있고, 선을 하나 이을 때마다 두 별 사이의 거리만큼의 비용이 듭니다.
- 별자리를 만드는 최소 비용을 구하는 문제입니다.
- 입력: 첫 번째 줄에 1보다 크거나 같고 100보다 작거나 같은 별의 개수 n이 주어지고 두 번째 줄부터 n개의 줄에는 각 줄의 x, y 좌표가 1000을 넘지 않는 양의 실수 형태로 주어지고, 최대 소수점 둘째자리까지 주어집니다.
- 출력: 첫 번째 줄에 정답을 출력합니다. 절대/상대 오차는 까지 허용합니다.
3. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Collections;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
static int n;
static int[] parents;
static double[][] stars;
static PriorityQueue<Edge> list;
static void input() {
Reader scanner = new Reader();
n = scanner.nextInt();
stars = new double[n][2];
for(int star = 0; star < n; star++) {
double x = scanner.nextDouble(), y = scanner.nextDouble();
stars[star][0] = x;
stars[star][1] = y;
}
}
static void solution() {
makeEdge();
double totalDist = kruskal();
System.out.println(String.format("%.2f", totalDist));
}
static void makeEdge() {
list = new PriorityQueue<>();
for(int star = 0; star < n - 1; star++) {
double startX = stars[star][0], startY = stars[star][1];
for(int other = star + 1; other < n; other++) {
double endX = stars[other][0], endY = stars[other][1];
double dist = Math.sqrt(Math.pow(endX - startX, 2) + Math.pow(endY - startY, 2));
list.offer(new Edge(star, other, dist));
}
}
}
static double kruskal() {
parents = new int[n];
for(int star = 0; star < n; star++) parents[star] = star;
double totalDist = 0;
for(int idx = 0; idx < n - 1; idx++) {
Edge e = list.poll();
int start = e.startIdx, end = e.endIdx;
double dist = e.dist;
if(isSameParents(start, end)) {
idx--;
continue;
}
union(start, end);
totalDist += dist;
}
return totalDist;
}
static int findParent(int star) {
if(parents[star] == star) return star;
return parents[star] = findParent(parents[star]);
}
static void union(int star1, int star2) {
int parent1 = findParent(star1), parent2 = findParent(star2);
if(parent1 != parent2) {
if(parent1 < parent2) parents[parent2] = parent1;
else parents[parent1] = parent2;
}
}
static boolean isSameParents(int star1, int star2) {
int parent1 = findParent(star1), parent2 = findParent(star2);
if(parent1 == parent2) return true;
return false;
}
static class Edge implements Comparable<Edge> {
int startIdx, endIdx;
double dist;
public Edge(int startIdx, int endIdx, double dist) {
this.startIdx = startIdx;
this.endIdx = endIdx;
this.dist = dist;
}
public int compareTo(Edge e) {
if(this.dist < e.dist) return -1;
else if(this.dist > e.dist) return 1;
else return 0;
}
}
public static void main(String[] args) {
input();
solution();
}
static class Reader {
BufferedReader br;
StringTokenizer st;
public Reader() {
br = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while(st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch(IOException e) {
e.printStackTrace();
}
}
return st.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
double nextDouble() {
return Double.parseDouble(next());
}
}
}4. 접근
- 각 별을 이은 직선을 나타내기 위해 Edge 클래스를 생성합니다.
- 직선으로 이은 두 별의 인덱스와 해당 직선의 거리를 멤버로 갖습니다.
- 주어진 별의 좌표들을 이용하여 두 별을 이은 모든 직선들을 구합니다.
static void makeEdge() {
list = new PriorityQueue<>();
for(int star = 0; star < n - 1; star++) {
double startX = stars[star][0], startY = stars[star][1];
for(int other = star + 1; other < n; other++) {
double endX = stars[other][0], endY = stars[other][1];
double dist = Math.sqrt(Math.pow(endX - startX, 2) + Math.pow(endY - startY, 2));
list.offer(new Edge(star, other, dist));
}
}
}- Kruskal 알고리즘을 이용하여 사이클이 발생하지 않는 선에서 거리가 짧은 순으로 n - 1개의 직선을 선택합니다.
- 직선을 거리가 짧은 순으로 하나씩 선택해보고 Union Find를 이용해 사이클이 생성되는지 확인하고 그렇지 않다면 해당 직선을 선택하고 사이클이 생성된다면 해당 직선은 선택하지 않고 다음 직선을 확인합니다.