1. 데이터(Data)와 자료형(Data Type)
데이터
- 컴퓨터의 입력 출력에 사용되는 것.
자료형
- 데이터 저장 및 연산을 위해 사용하는 것.
- 데이터를 효율적으로 다룰 수 있도록 함.
- 저장될 값의 유형과 크기에 맞게 선택.
종류
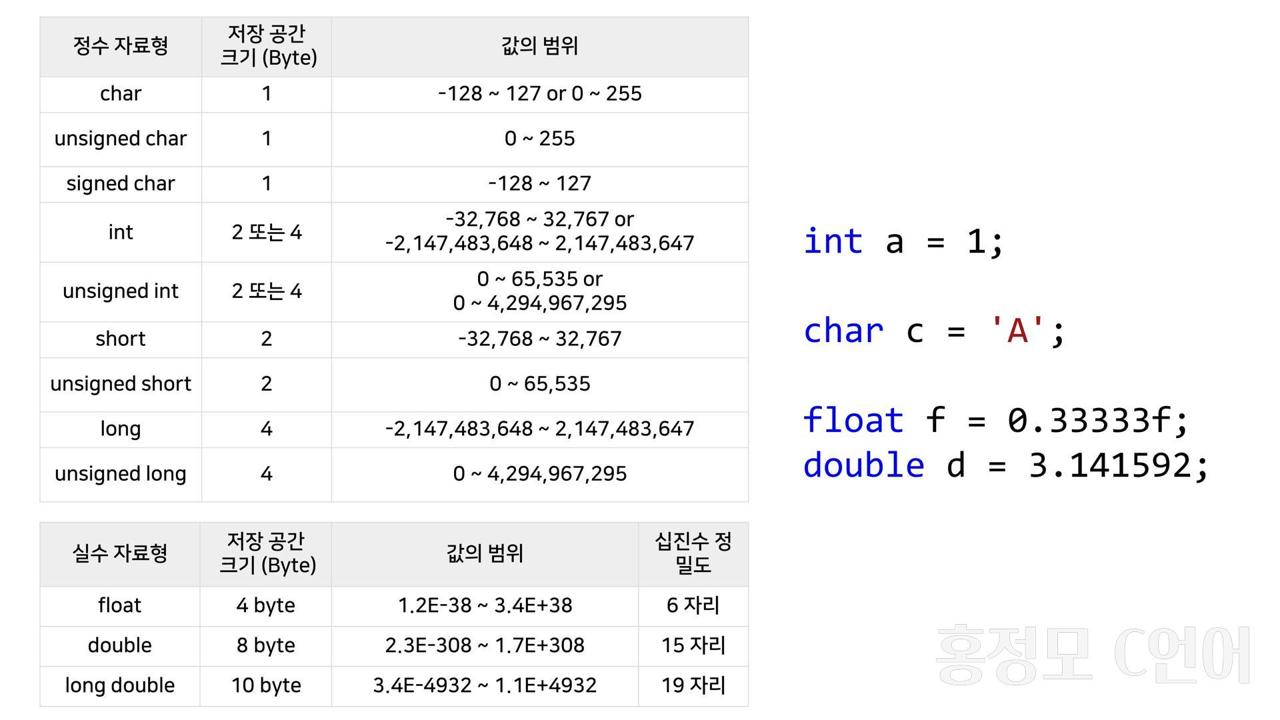
- 정수 자료형
int a = 1; // 변수 a의 값 = 1 이고 int 자료형 할당
char c = 'A'; // 변수 c의 값 = 'A' (문자)이고 char 자료형 할당💡 문자의 자료형은?
- 컴퓨터는 문자도 정수로 인식하여 사용하기 때문에, 문자도 정수 자료형에 포함된다.- 실수 자료형
float f = 0.3333f; // 변수 f의 값 = 0.3333f 이고 float 자료형 할당
double d = 3.141592; // 변수 d의 값 = 3.141592 이고 double 자료형 할당2. 변수와 상수
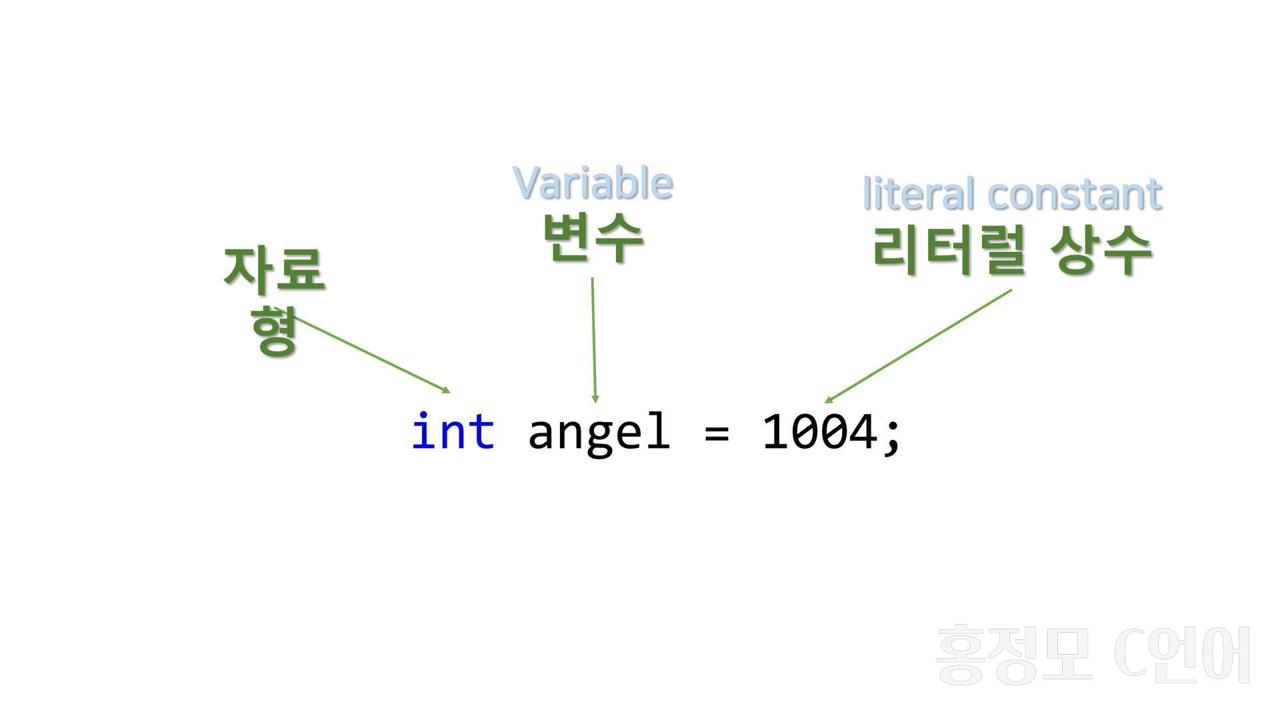
변수(Variable)
- 값을 저장할 수 있는 Memory 공간.
- 저장되는 값이 변할 수 있음.
상수(Constant)
- 변하지 않는 값.
1) 리터럴 상수(Literal constant)
- 문자 그대로의 상수.
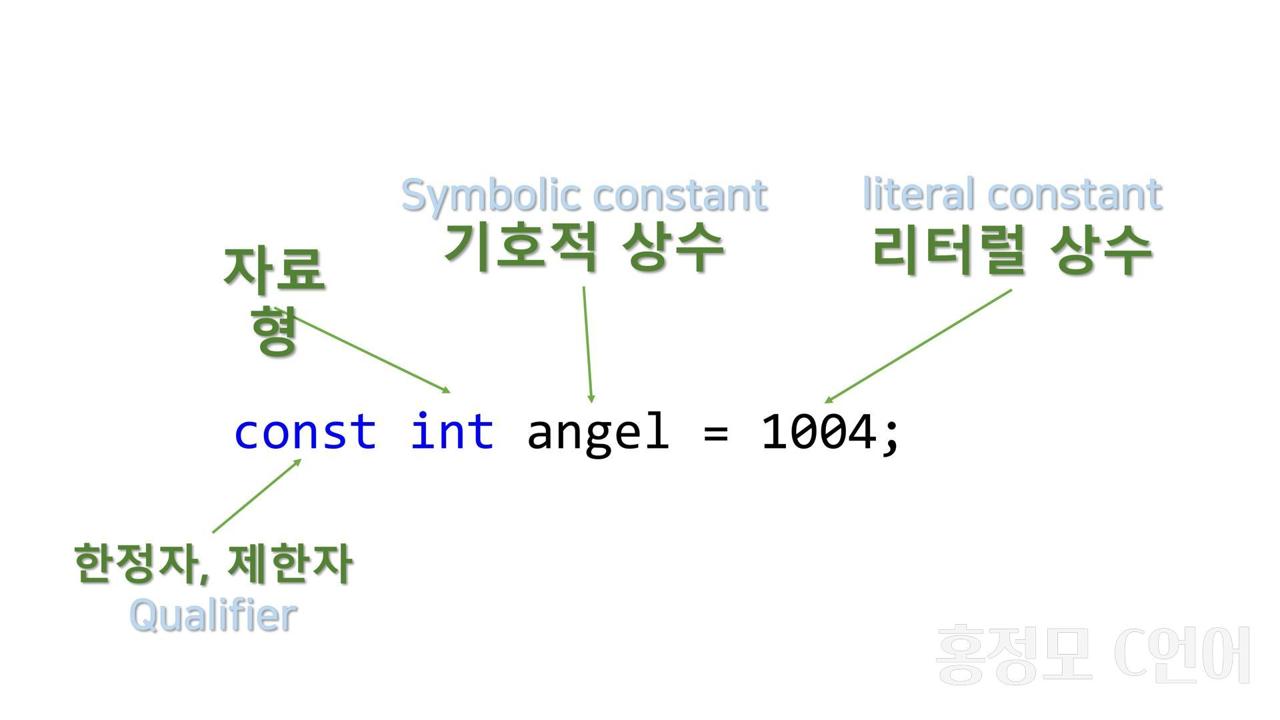
2) 기호적 상수(Symbolic constant)
- 자료형 앞에 const 를 붙여 변수를 상수로 바꾼 것.
3. 정수와 실수
정수(Integers)
- 음의 정수, 0, 양의 정수를 나타냄.
- 컴퓨터 내부적으로는 2진수로 되어있음.
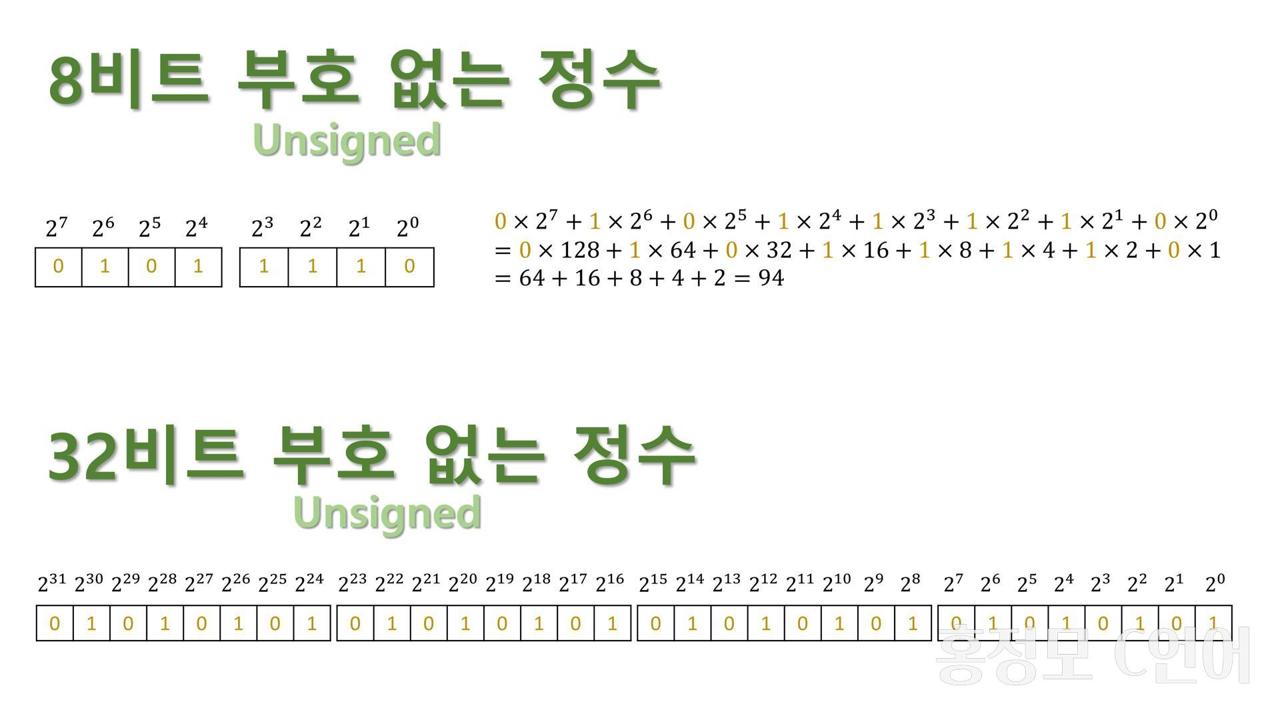
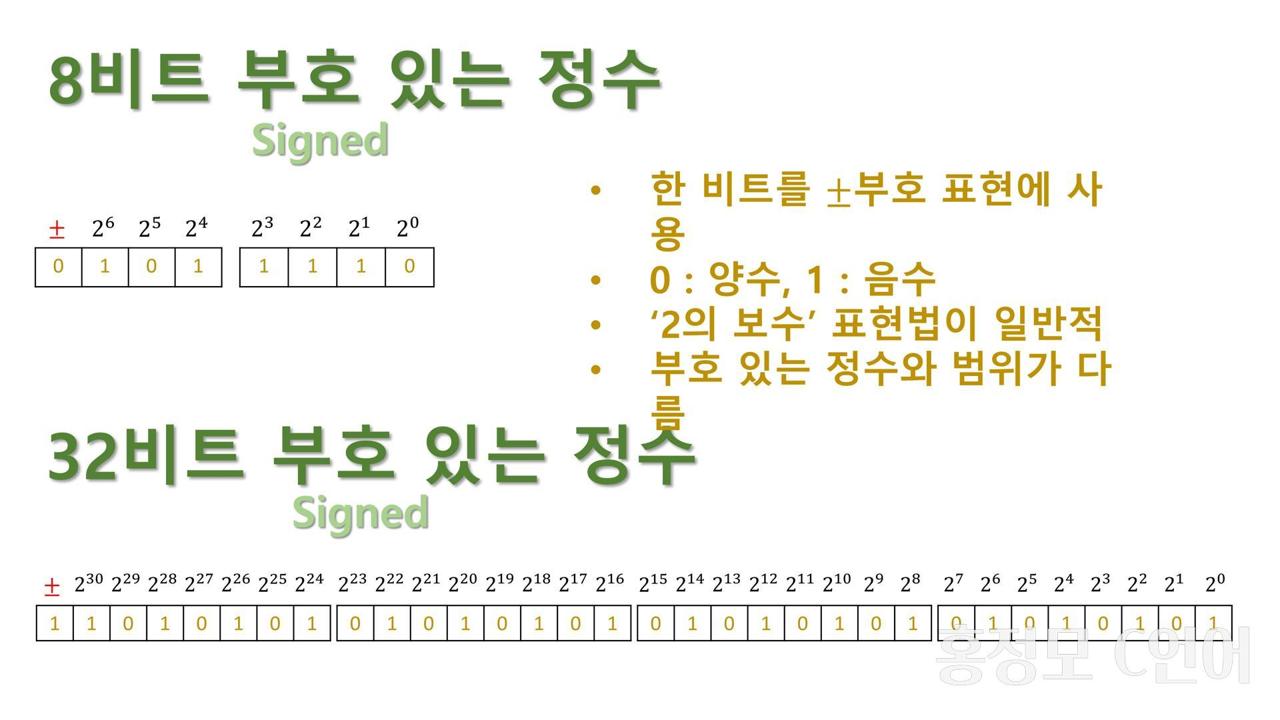
1. 부호 없는 정수(Unsigned)
- 부호가 없는 양의 정수라고 판단하며, 값이 0 부터 시작.
- 최상위 비트를 부호비트로 사용하지 않음.
Ex) Unsigned int 자료형의 정수 범위 = 0 ~ 4,294,967,295
2. 부호 있는 정수(Signed)
- 부호가 있는 정수라고 판단.
- 최상위 비트를 부호비트로 사용. (1인 경우 음수)
- 음수를 표현할 때 2의 보수 형식을 사용.
- Ex) Signed int 자료형의 범위 = -2,147,483,648 ~ 2,147,483,647
실수(Real Numbers)
- 소수점을 포함한 수를 나타냄.
- 컴퓨터 내부적으로는 2진수로 되어있음.
- C 언어에서 실수 계산 및 표현을 위해 부동소수점 표현법 사용.
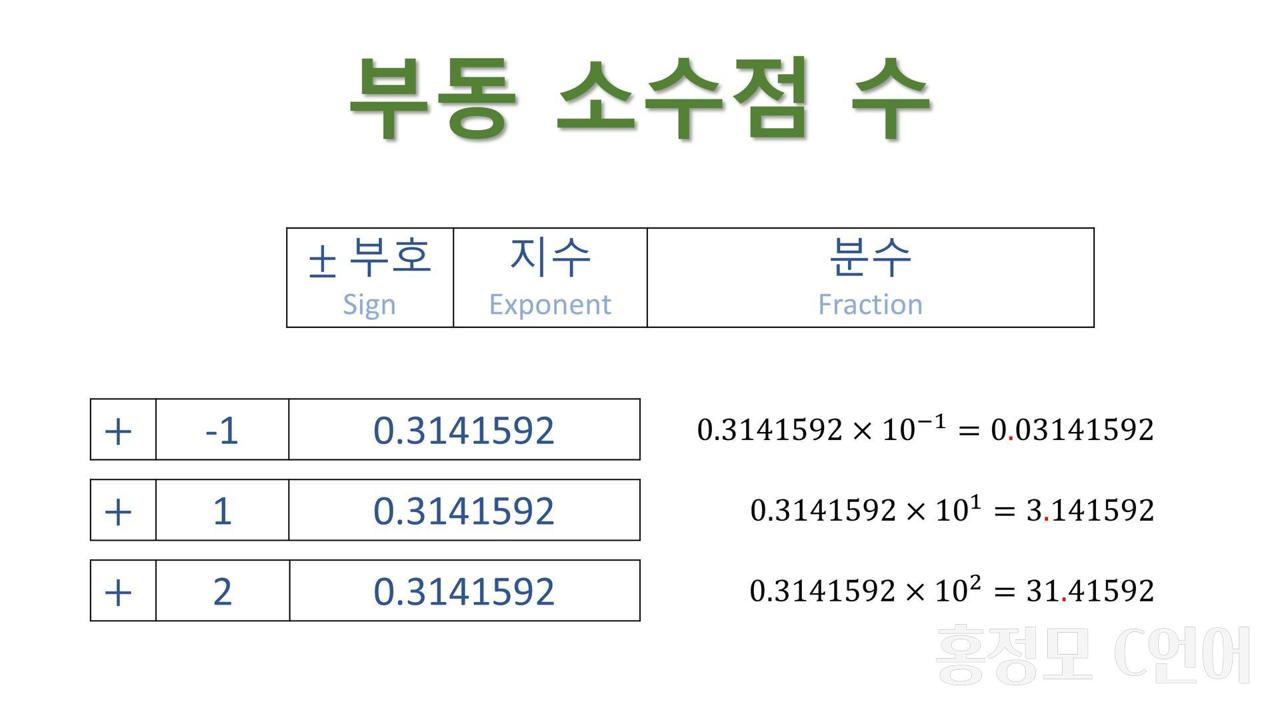
- 부동소수점 = 소수점 위치를 나타내는 방법.
Ex) 3.14 = 3.14E0 = 3.14e0 = 0.314E1 - e, E = 지수(Exponent) = 10의 거듭제곱.
- 0.314E1 = 0.314 x 10^1 = 3.14
실수 자료형에 따른 Memory 할당 방법
( 부호(Sign) | 지수(Exponent) | 분수(Fraction) )
- float (32 bit)
- 부호 : 1 bit
- 지수 : 8 bit
- 분수 : 23 bit
- double (64 bit)
- 부호 : 1 bit
- 지수 : 11 bit
- 분수 : 52 bit
4. 정수의 오버플로우(Overflow)
- 값이 정수 자료형의 크기를 넘어가는 것.
- 오버플로우가 발생하면 예기치 않은 문제가 발생.
정수 덧셈 오버플로우
- 특정 정수 자료형에 들어갈 수 있는 최대값에 1이 더해지면, 그 결과는 0이 됨.
Ex) unsigned int
- (2진수) 최대값 + 1 = 11111111111111111111111111111111 + 1 = 10000000000000000000000000000000
- 최상위 1비트는 덧셈으로 인해 새로 생긴 비트이며, int 자료형의 크기를 벗어나므로 버려진다.
- 즉, 값은 0(0b0000000000000000000000000000000) 으로 저장된다.
정수 뺄셈 오버플로우
- 특정 정수 자료형에 들어갈 수 있는 최소값에 1을 빼면, 그 결과는 자료형의 최대값이 됨.
Ex) unsigned int
- (2진수) 최소값 - 1 = 0000000000000000000000000000000 - 1 = 10000000000000000000000000000000
- 뺄셈시, 최상위 비트에 1이 있다고 가정하에 계산 됨.
- 10000000000000000000000000000000 - 1 = 11111111111111111111111111111111
- 즉, 최대값(11111111111111111111111111111111)이 저장되게 된다.
5. 문자형
- 컴퓨터는 문자도 숫자로 인식.
- 문자형도 정수형의 일부인 것처럼 분류하는 것이 일반적.
- 어떤 문자가 어떤 숫자에 대응이 되는지 정해놓은 규칙 = ASCII 코드.
6. 부동소수점형
과학적 표기법(Scientific Notations)
- 천문학적으로 큰 숫자를 다루기 위해 사용.
- 표기법 = m x 10^n
- m = significand(앞에 있는 수), n = exponent(지수)
Ex) 123.45 = 12345 x 10^-2 = 1.2345 x 10^2 - 유효 숫자 : significand 에서 믿을 수 있는 숫자 개수. (왼쪽부터)
Normalized significand
- 컴퓨터에서 실수를 부동소수점 자료형으로 저장할 때 사용하는 형태.
Ex) 1.XXXX x 2^?
4 바이트 부동소수점 저장 방식 (IEEE 표준)
- 부호(Sign) - 1 bit
- 0 = 양수, 1 = 음수
- 지수(Exponent) - 8 bit
- 부동소수점 지수 값(n)은, Unsigned Exponant를 사용한다음 그 값에 127을 뺀 후 저장.
- Unsigned를 사용하는게 비교가 더 빠르다고 함.
Ex) Unsigned Exponant = 0일 경우 n = -127
- 분수(Fraction) - 23 bits
- Significand 에서 소수점 아래 부분.
- 순서는 왼쪽부터 2^-1, 2^-2...
💡 부동소수점 표현 방법은 메모리를 쪼개서 사용하는 것이기 때문에 주의할 필요가 있음.정수와 부동소수점 범위 비교
- 4 바이트 정수 범위
- -2,147,483,648 ~ 2,147,483,647
- 대략 -2.14 x 10^9 ~ 2.14 x 10^9
- 4 바이트 부동소수점 범위
- 대략 -3.4 x 10^38 ~ 3.4 x 10^38
💡
즉, 같은 4 바이트를 사용하더라도 부동소수점이 범위가 훨씬 넓다.
! 부동소수점은 메모리를 쪼개서 쓰기 때문에 정밀도를 표현할 수 있는 10진수 유효숫자가 6개밖에 되지 않는다.7. 부동소수점의 한계
round-off errors (Ex1)
- 범위가 너무 많이 차이나는 숫자를 연산하면 오류가 생김.
#include <stdio.h>
int main()
{
float a, b;
a = 1.0E20f + 1.0f; // 범위가 많이 차이나는 숫자 연산
b = a - 1.0E20f; // 예상되는 b의 값 = 1.0
printf("%f\n", b); // 확인 결과 b의 값 = 0으로 확인 됨.
return 0;
}round-off errors (Ex2)
- 0.01을 100번 더했을 때, 결과 값이 1이 아닌 0.999999로 나타남.
- 부동소수점은 실수(0.01)를 정확하게 만들지 못하고 근사 값(0.009999999776f)을 만들기 때문에, 그 근사 값 만큼의 오차 발생.
- fraction 부분인 2^-1, 2^-2, 2^-3... 을 사용해서 10진수를 만들어내야 되기 때문에, 정확하게 만들 수가 없음. (부동소수점의 한계)
#include <stdio.h>
int main()
{
float a = 0.0f; // 실수형 변수 a 초기화
for (int i = 0; i < 100; ++i)
{
a = a + 0.01f; // a에 0.01을 100번 더함
}
printf("%f\n", a); // 예상되는 a의 값은 1 이지만, 실제로는 0.99999로 나타남
return 0;
}overflow
- 정수형에서의 오버플로우와 다름.
- 자료형의 최대값보다 높은 숫자일 경우, "inf"(infinite)가 출력되며 문제가 발생.
- 값을 "0"으로 나누는 경우에도 "inf"가 발생.
#include <stdio.h>
int main()
{
float max = 3.402823466e+38F; // 실수형 변수 max에 실수 자료형 최대 값 대입.
max = max * 100.0f; // max 값에 100을 곱함.
printf("%f\n", max); // max 값 출력시 inf로 나타남
return 0;
}underflow
- 자료형의 최소값보다 낮은 숫자일 경우, 값을 0으로 만드는 "subnormal"이 발생된다.
- "subnormal" = 정밀도의 한계를 넘어버림.
#include <stdio.h>
int main()
{
float min = 1.401298464e-45F; // 실수형 변수 min에 실수 자료형 최소값 대입
min = min / 2.0f; // min 값을 2로 나눔.
printf("%e\n", min); // subnormal이 발생하여 숫자를 표현하지 못해 결과는 0으로 나타남.
return 0;
}8. 불리언형
- 고전 C 언어에는 존재하지 않음.
- 최근에 불리언형이 새로 추가 됨. (_Bool)
- 0이면 False, 1이면 True.
- 1 bit만 사용해도 문제가 되지 않지만, 자료형이 기본 크기가 byte 이기 때문에 (Memory 주소의 기본 단위이기 때문) 불리언형의 크기는 1 byte.
- stdbool.h 라이브러리를 추가해주면, 불리언형 변수 선언 가능.
💡 컴퓨터의 True, False 판단 방법 = False가 아니면 True다._Bool 사용
#include <stdio.h>
int main()
{
_Bool b1 = 0;
printf("%d", b1);
return 0;
}stdbool.h 라이브러리 사용
#include <stdio.h>
#include <stdbool.h>
int main()
{
bool b1 = 0;
printf("%d", b1);
return 0;
}🚩 출처 및 참고자료 : 홍정모의 따라하며 배우는 C 언어 (따배씨)