시간복잡도, 공간복잡도, 빅오 표기법
이 글에서는, 시간 복잡도와 공간 복잡도의 개념을 설명하고, 표기법 중 빅오 표기법을 예제를 통해서 알아보는 시간을 가져보겠습니다.
시간 복잡도
컴퓨터 프로그램의 입력값과 연산 수행 시간의 상관관계를 나타내는 척도. 즉, 알고리즘의 수행시간 분석결과이다.
주로 점근 표기법으로 나타내며, O(빅오), Ω(오메가), Θ(세타) 표기법 중 빅오와 빅세타 표기법이 많이 사용된다.
그 중에서, 가장 많이 사용되어지는 빅오(Big-O) 표기법에 대해서 알아보자.
빅오 표기법(Big-O notation)
알고리즘의 입력 크기에 대해 수행 시간이 어떤 방식으로 증가하는지를 표기하는 것으로 최악의 경우의 시간 복잡도를 의미한다.
여기서 중요한 것은 최악의 경우를 고려한다는 것인데, 그 이유는 최악의 경우에도 효율적으로 동작한다면, 어떤 입력이 주어지더라도 동작 예측이 가능하다는 점과 사용 환경의 예측 불가능성으로 인해 최악의 경우에 대비한다면 안정성을 유지하는 데 큰 도움이 된다는 것 때문이다.
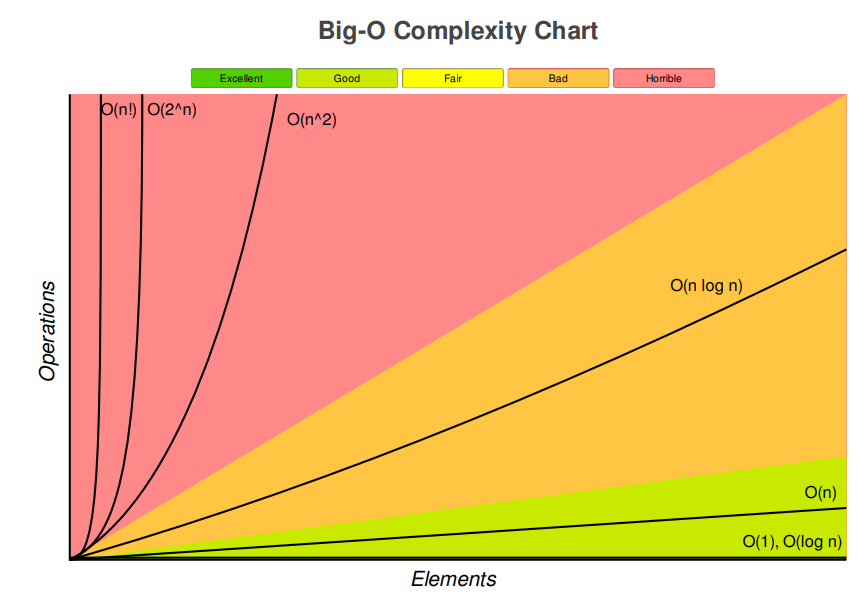
빅오 표기법 순서
시간 복잡도와 로직의 수행 시간은 비례하므로 시간 복잡도 수치가 작을수록 효율적인 알고리즘을 뜻한다. 위로 갈수록 간단하고, 아래로 갈수록 복잡하다.
-
O(1)과 같은 상수(constant)
-
O(logn)과 같은 로그(logarithmic) //
log n은log2 n을 뜻한다 -
O(n)과 같은 선형
-
O(nlogn) 과 같은 선형로그
-
O(n^c), O(n^3)과 같은 다차(polynomial)
-
O(c^n), O(3^n)과 같은 지수(exponential)
-
O(n!)과 같은 팩토리얼(factorial)
빅오 표기법 규칙
알고리즘 성능을 표현하는 일반적이고 간결한 표기를 제공하기 위해서 빅오 표기법에는 몇가지 규칙이 존재하는데, 그 규칙에 대해 알아보자.
1. 계수법칙
f(n)이 O(g(n)) 이라면, kf(n)은 O(g(n)) 이다. (단, 상수 k > 0)
말로만 보면 이게 무슨말인가 싶으니, 바로 코드로 보자.
function coefficient_rule(n) {
let count = 0;
for (let i = 0; i < n; i++) {
count = count + 1;
}
return count;
}위 코드는 입력 크기 n에 비례하여 반복이 실행되기 때문에,시간복잡도가 O(n)이다.
너무간단한가? 그렇다면 밑에 다른 예제를 하나 더 살펴보자.
function coefficient_rule2(n) {
let count = 0;
for (let i = 0; i < 5 * n; i++) {
count = count + 1;
}
return count;
}위 코드는 f(n)=5n이다. 그러면 시간복잡도는 O(5n)인가? 아니다, 시간복잡도는 O(n)이다. 반복문의 횟수는 5n번 이지만, 빅오 표기법에서는 상수 계수를 무시하기 때문이다. 그렇다면 다시 한 번 밑에 코드를 살펴보자.
function coefficient_rule3(n) {
let count = 0;
for (let i = 0; i < n; i++) {
count = count + 1;
}
count = count + 1;
return count;
}위 코드의 시간복잡도는 어떨까? 위 두개의 예제와 마찬가지로 O(n)이다. 반복문이 n번 실행되고, 반복문 외부에서 상수 시간 작업이 한 번 수행되기 때문에, 상수항은 무시되므로 O(n)이다.
2. 합의 법칙
f(n)이 O(h(n))이고 g(n)이 O(p(n))이면 f(n)+g(n)은 O(h(n)+p(n))이다.
- 합의 법칙을 적용한 다음엔 반드시 계수법칙을 적용해야 한다.
function sum_rule(n) {
let count = 0;
for (let i = 0; i < n; i++) {
// (1) f(n) = n
count = count + 1;
}
for (let i = 0; i < 5 * n; i++) {
// (2) f(n) = 5n
count = count + 1;
}
return count;
}- 위 코드에서
n + 5n = 6n이므로f(n)=6n이지만, 상수항은 무시되므로 시간복잡도는O(n)이다.
3. 곱의 법칙
f(n)이 O(h(n)) 이고, g(n)이 O(p(n))이라면 f(n)g(n)은 O(h(n)p(n)) 이다.
- 곱의 법칙도 합의 법칙과 마찬가지로, 곱의 법칙을 적용한 다음엔 반드시 계수법칙을 적용해야 한다.
function multiplication_rule(n) {
let count = 0;
for (let i = 0; i < n; i++) {
count = count + 1;
for (let j = 0; j < 5 * n; j++) {
count = count + 1;
}
}
return count;
}- 위 코드에서는
f(n) = 5n*n => 5n^2이므로 시간복잡도는O(n^2)가된다.
4. 다항 법칙
f(n)이 k차 다항식이면 f(n)은 O(n^k)
function polynomial_rule() {
let count = 0;
for (let i = 0; i < n * n; i++) {
count = count + 1;
}
return count;
}- 위 코드에서
f(n)=n^2이므로 시간복잡도는O(n^2)가 된다.
시간 복잡도 예제
예제를 통해서 다양한 시간 복잡도를 알아보자, 순서는 처음부터 효율이 좋고 뒤로 갈수록 효율성이 감소하는 순서이다.
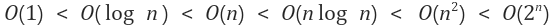
O(1) 과 같은 상수(constant)
// O(1)
function constantTime(arr) {
return arr[0];
}O(logn) 과 같은 로그(logarithmic)
log n 은 log2 n 을 뜻한다
// O(log n)
function logarithmicTime(n) {
let result = 1;
while (n > 1) {
n = Math.floor(n / 2);
result *= 2;
}
return result;
}O(n) 과 같은 선형
// O(n)
function linearTime(arr) {
let sum = 0;
for (let num of arr) {
sum += num;
}
return sum;
}O(n log n) 과 같은 선형로그
// O(n log n)
function linearLogarithmic(arr) {
for (let i = 0; i < arr.length; i++) {
let valueToSearch = arr[i];
let low = 0;
let high = arr.length - 1;
while (low <= high) {
let mid = Math.floor((low + high) / 2);
if (arr[mid] === valueToSearch) {
console.log("Found:", valueToSearch);
break;
} else if (arr[mid] < valueToSearch) {
low = mid + 1;
} else {
high = mid - 1;
}
}
}
}- 외부 루프의 시간복잡도
O(n), 내부 루프에서 이진 검색O(log n).
O(n^c), O(n^3)과 같은 다차(polynomial)
// O(n^2)
function quadraticTime(arr) {
let num = 1;
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length; j++) {
num *= arr[i] * arr[j];
}
}
return num;
}O(c^n), O(3^n)과 같은 지수(exponential)
// O(2^n)
function fibonacci(n) {
if (n <= 1) {
return n;
} else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}공간 복잡도
프로그램이 얼마만큼의 메모리를 사용하는지를 나타내는 지표. 즉, 알고리즘이나 프로그램을 실행하는 데 필요한 메모리의 양을 나타낸다.
-
공간 복잡도는 일반적으로 알고리즘의 시간 복잡도와 함께 고려되며 알고리즘이 실행되는 환경에 따라 달라질 수 있다. 예를 들어, 시간 복잡도가 낮은 알고리즘은 실행하는 데 더 많은 메모리가 필요할 수 있지만 공간 복잡도가 낮은 알고리즘은 실행하는 데 더 오래 걸릴 수 있다.
-
최근에는 하드웨어 메모리 용량이 많이 좋아졌기 때문에 시간복잡도가 더 우선시된다.
공간 복잡도 예제
공간 복잡도는 일반적으로 시간복잡도와 마찬가지로 빅오 표기법으로 표시한다.
O(1) - 상수 공간 복잡도
function constantSpace(n) {
let x = 10; // 상수 크기의 메모리 사용
return x + n;
}- 위 예제는 입력
n에 관계없이 항상 상수 크기의 메모리만 사용하므로, O(1)의 공간 복잡도를 가진다.
O(n) - 선형 공간 복잡도
function linearSpace(n) {
let arr = new Array(n); // 배열 크기가 n인 메모리 사용
for (let i = 0; i < n; i++) {
arr[i] = i;
}
return arr;
}- 입력
n에 비례하여 배열 크기가 선형으로 증가하므로O(n)의 공간 복잡도를 가진다.
O(n^2) - 다항식 시간 복잡도
function quadraticSpace(n) {
let matrix = [];
for (let i = 0; i < n; i++) {
matrix[i] = new Array(n); // 2차원 배열, 크기가 n * n
for (let j = 0; j < n; j++) {
matrix[i][j] = i + j;
}
}
return matrix;
}- 2차원 배열을 사용하며, 배열의 크기가
n * n으로 증가하므로O(n^2)의 공간 복잡도를 가진다
