트러블 슈팅_1

charlie_·2021년 9월 9일

부제: 클로저와 무한 스크롤

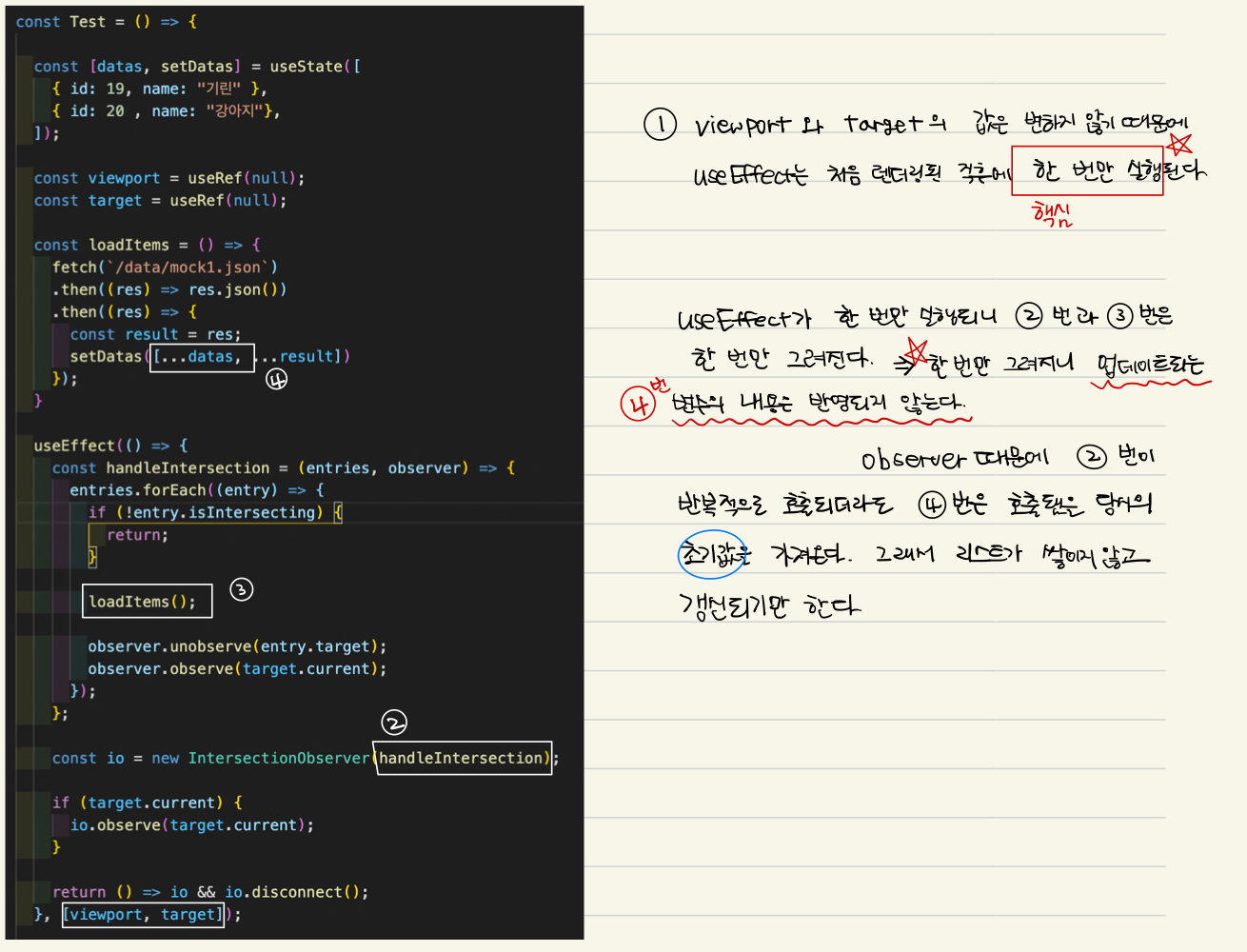
문제

observer의 관찰대상이 드러날 때 loadItems 함수가 반복적으로 호출되는 것까지는 확인했지만, datas에 데이터가 쌓이지 않고 초기값 아래에 새로운 값으로 갱신되기만 하는 문제가 있었다.

원인

useEffect가 한 번만 호출되며, loadItems 함수가 외부 변수를 기억하고 있는 것이 원인이었다.

loadItems 함수는 useEffect가 호출될 때마다 새로 그려지는데, useEffect가 한 번만 호출되며 loadItems 함수는 새로 그려지지 않는다. 그렇기때문에 loadItems 함수는 처음에 그려질 당시의 외부 변수값을 기억해두고 호출될 때마다 꺼내 사용한다.

해결 방법

useEffect가 원할 때마다 호출되도록 dependency를 바꾼다.
loadItems 함수에 외부 변수를 사용하지 않는다.

결과

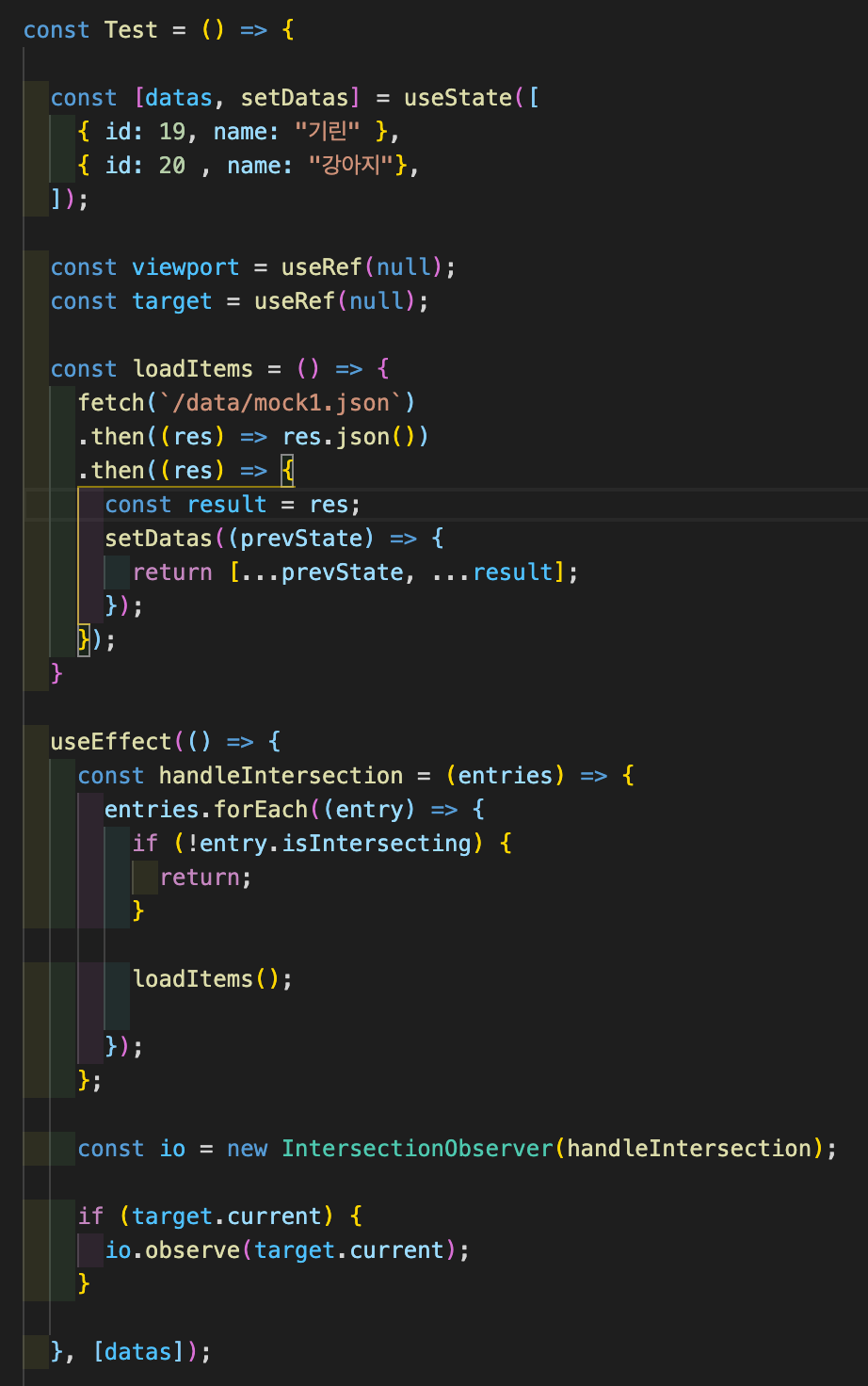
datas가 업데이트될 때마다 useEffect가 호출되도록 dependency를 변경.
외부 변수에 영향을 받지 않도록 매개 변수 활용.

설명

직관적인 이해를 돕기 위해 연욱님께서 코드샌드박스에 작성하신 코드를 몇 줄 빌려왔다. 사이트에 방문해서 직접 버튼을 클릭해보면 이해에 큰 도움이 될 듯하다.

function Home() {
  const [count, setCount] = useState(0);

  const asyncUpdate = () => {
    setTimeout(() => {
      // setCount(count + 1); // 이상한데?
      // setCount((prev) => prev + 1); // 원하는 대로 나오는걸?
    }, 2000);
  };

  const immediateUpdate = () => {
    setCount(count + 1);
  };

  return (
    <div>
      <h2>count:{count}</h2>
      <button onClick={asyncUpdate}>asyncUpdate</button>
      <button onClick={immediateUpdate}>immediateUpdate</button>
    </div>
  );

여기 2초에 1번, 자동으로 1을 더하게 만드는 버튼과 누르는 즉시 1을 더하는 버튼이 있다. 그리고 setTimeout함수 안에 외부 변수를 사용할 때와 사용하지 않을 때의 차이를 나타내는 각각의 코드가 있다.

setCount(count + 1)
:: asyncUpdate버튼을 누른 후 immediateUpdate버튼을 여러번 누르다보면 숫자가 잘 올라가다가 갑자기 뚝 떨어지는 모습을 볼 수 있다.
setCount((prev) => prev + 1)
:: 위의 코드와는 달리 숫자가 누르는 대로 자연스럽게 올라가는 모습을 볼 수 있다.

함수가 호출될 때마다 외부 변수에서 업데이트된 값이 아닌 초기값만 가져오는 문제가 있음을 알 수 있다. 외부 변수를 기억하는 것은 클로저 함수의 특징이다.

클로저

외부 변수를 기억하고 이 외부 변수에 접근할 수 있는 함수를 말한다.
출처: 코어 자바스크립트

클로저를 이해하기 위해서는 스코프 체인과 렉시컬 스코프, 그리고 실행 컨텍스트와 렉시컬 환경에 대한 사전 지식이 필요하다.

1. 스코프 체인부터 시작해보자.

사전 지식
:: 스코프는 함수 단위로 생성된다.
:: 밖에 있는 변수를 내부에서 사용하는 것은 가능하다.
(내 집 안에서는 밖에 있는 물건을 가져다가 쓸 수 있는데, 밖에서 다른 집 안에 있는 물건을 가져올 수는 없는 것처럼....?)

let d = 4;

function  outer() {
  let c = 3;
  let b = 2;
 
  function inner() {
    let b = 1;
    let a = 0;

    console.log(d);
  }

  inner();
}

outer();

실행되는 과정

1) outer함수를 호출하면 inner함수가 자동으로 호출된다. 

2) inner함수에서 console.log(d)가 실행된다.

3) 이 때 변수 d를 찾기 시작하는데, 스코프를 기준으로 탐색을 한다.

4) console.log(d)가 호출된 inner함수의 스코프에서 제일 먼저 변수 d를 찾는다.

5) 없다면 outer함수의 스코프에서 변수 d를 찾는다.

6) 없다면 전역 스코프에서 변수 d를 찾는다.

7) 있다면 변수 d의 값을 반환하고, 없다면 에러를 띄운다.

정리
:: 변수(d)를 찾기 위해 연결된 스코프(inner → outer → 전역)를 타고 올라가야한다는 것을 알 수 있다. 이처럼 변수를 찾을 때는 연결된 스코프를 타고 올라가며 찾으라는 규칙이 바로 스코프 체인이다.

2. 렉시컬 스코프

사전 지식
:: 스코프는 함수 단위로 생성된다.
:: 렉시컬 스코프는 상위 스코프를 결정하는 방식이다.
:: 렉시컬 스코프는 호출되는 위치가 아니라 선언되는 위치에 따라 결정된다.

출처: 모던 자바스크립트 Deep Dive

var x = 1;

function foo() {
  var x = 10;
  bar();
}

function bar() {
  console.log(x);
}

foo(); // 10
bar(); // 1

실행되는 과정

1) bar는 전역에서 선언되었지만, foo함수 안에서 호출되었다.

2) 이 때 렉시컬 스코프 방식을 따를 경우 bar가 선언된 전역 스코프가 bar의 상위 스코프가 된다.

3) bar함수가 호출되었을 때 bar함수 내부 스코프에 변수 x가 있는지 확인한다.

4) 없다면 스코프 체인 규칙에 따라 상위 스코프인 전역 스코프에 변수 x가 있는지 확인한다.