1. GCD(Great Common Divisor)

최대 공약수를 구하는 문제가 가끔 출제되고는 한다. 그중에서 가장 효율적으로 구현하는 방법은 유클리디안 호제법을 이용한 것이다. 코드는 다음과 같다

int gcd(int a, int b){ 
// Great Common Divisor, 유클리디안 호제법 이용
    if(a==0) return b;
    return gcd(b % a, a); 
}

위의 코드는 숫자 입력의 제한이 없다. 더 작은 수가 먼저 들어와도 상관 없고, 큰 수가 들어와도 상관이 없다.

2. LCM(Lowest Common Multiple)

최소 공배수는 위의 GCD를 활용하여 구현한다.

int lcm(int a, int b){
    return (a * b)/gcd(a,b);  
}

두 수를 곱해버린뒤, 중복되는 최대공약수로 나누어 버리면된다.

3. 소수 구하기

3.1. 에라토스테네스의 채

에라토스테네스의 채는 소수를 구하는 빠른 알고리즘이다. 모든 숫자에 대해서 하나씩 확인하는 것 보다 훨씬 빠르다. 기본적으로 각각의 숫자에 대해서 배수를 제거해 나가는 식이다.

const int max_n = 40;
bool che[max_n + 1];

vector<int> era(int mx_n){ 
// 에라토스테네스의 채 , 배수를 지워나가는 방식 
    vector<int> v;
    for( int i = 2; i <= mx_n; i++){
        if(che[i]) continue;
        for( int j = 2*i; j <= mx_n; j+= i){
            che[j] = 1;
        }
    }
    for( int i = 2; i <= mx_n; i++) if(che[i] == 0 ) v.push_back(i);
    return v;
} 

이렇게 하면 시간 복잡도는 감소하지만, 메모리를 계속해서 잡고 있게 된다. 찾고자 하는 숫자가 작다면 가능하지만, 백만 이상으로 넘어가게 되면 해당 방식은 어려울 수 있다.

3.2. 매번 확인

위와 같은 메모리의 문제가 생기는 경우 각각의 숫자에 대해서 확인하는 방식으로 진행해야 한다.

bool check(int n){ 
    if( n <= 1) return 0;
    if( n == 2) return 1;
    if( n % 2 == 0) return 0;
    for( int i =2 ; i*i <=n ; i ++){
        if( n % i == 0) return 0;
    }
    return 1;
}

4. 등차, 등비수열의 합

4.1. 등차수열의 합

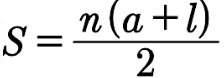
n = 원소의 개수 // a = 시작 값// l = 마지막 값

n * (a + l) / 2 

4.2 등비수열의 합

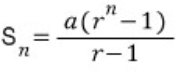
r = 비

a * ((int)pow(r, n)) - 1) / (r-1)

5. n승, 제곱근

cout << "sqrt" << endl;
cout << sqrt((int)pow(2, 4))<<endl;