
1. Recursive Function
재귀 함수란 정의 단계에서 자신을 재참조 하는 함수를 의미. 주로 문제를 작은 부분으로 나누어서 풀 때 활용한다.
대표적인 예시로 펙토리얼과 피보나치 수열이 존재한다.
#include <iostream>
using namespace std;
int factorial(int n){
if (n == 0 || n == 1) return 1;
return n * factorial(n-1);
}
int main(){
cout << "Factorial" << endl;
cout << factorial(5) << endl << endl;
}재귀함수를 사용하는 경우 반드시 종료조건을 달아 주어야 하며, 사이클이 존재하는 경우 사용해서는 안된다.
또한 반복문으로 가능한 경우, 반복문이 함수 호출에 대한 cost를 save할 수 있어서 유리하다.
2. Permutation
서로 다른 n개의 원소에서 r개를 중복없이 순서에 상관있게 선택하는 혹은 나열하는 것을 순열이라고 한다.
순열의 식은 아래와 같다.
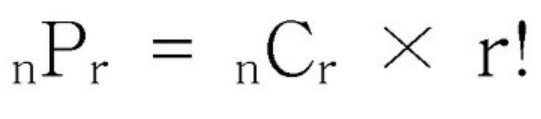
2.1. next_permutation()
next_permutation() 함수를 사용해서 간단하게 순열을 구현할 수 있다.(algorithm 라이브러리에 있음)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main(){
cout << "Permutation" << endl;
vector<int> v;
for(int i : a) v.push_back(i);
do{
cout << v[0] << v[1] << v[2] << endl;
}while(next_permutation(v.begin(), v.end()));
cout << endl;
do{
cout << v[0] << v[1] << v[2] << endl;
}while(next_permutation(v.begin(), v.begin() + 2)); // 앞에 두개만 고치게 된다.
cout << endl;
cout<< "unsorted case" << endl;
int b[3] = {2,1,3};
v.clear();
for ( int i : b) v.push_back(i);
do{
cout << v[0] << v[1] << v[2] << endl;
}while(next_permutation(v.begin(), v.end())); // 그 다음번째 순열을 만들어내기 때문에 정렬되지 않은 상태로 진행하면 문제가 발생할 수 있다.
cout<< endl;
sort(v.begin(), v.end());
do{
cout << v[0] << v[1] << v[2] << endl;
}while(next_permutation(v.begin(), v.end()));
cout<< endl;
}이때 유의할 점은 반드시 정렬을 진행하고 사용해야 한다는 점이다.
next_permutation() 함수는 그 다음번째 순열을 만들어주는 함수 이기에, 정렬을 진행하지 않고 진행한다면, 우리가 원하지 않는 결과를 얻을 수도 있다.
배열에 대해서 진행하는 경우 다음과 같이 구현 가능하다.
do{
cout<< a[0] << a[1] << a[2] << endl;
}while(next_permutation(&a[0], &a[3]));
do{
cout<< a[0] << a[1] << a[2] << endl;
}while(next_permutation(&a[0], &a[0] + 3));
do{
cout<< a[0] << a[1] << a[2] << endl;
}while(next_permutation(a, a + 3)); // 위의 세개 모두 동일한 코드. 항상 시작 주소, 마지막 주소 +1 로 넣어주면 된다.
cout << endl;2.2. 재귀 함수로 permutation 구현
아래와 같은 방법으로 직접 재귀함수를 만들어 주는 방법도 가능하다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int a[3] = {1,2,3};
void makePermutation(int n,int r, int depth){
if( r == depth) {
cout << a[0] << a[1] << a[2] << endl;
}
for(int i = depth; i < n; i++){
swap(a[i], a[depth]);
makePermutation(n,r, depth + 1);
swap(a[i], a[depth]);// 원본으로 회귀
}
}
int main(){
cout << "Permutation with Recur" << endl;
makePermutation(3,3,0);
}포인트는 재귀 함수를 호출 한 뒤에 호출하기 전으로 되돌려준다는 점이다.
depth가 증가함에 따라 시작점 증가, 시작 점 다음 부터 한칸씩 swap해 나가는 구조이다.
출력되는 순서를 생각해보면
123 >> 132 >> 213 >> 231 >> 321 >> 312 순이다.
3. Combination
서로 다른 원소를 가진 집합에서 원소들을 택하여 만든 부분집합을 조합이라 부른다.
조합의 식은 아래와 같다
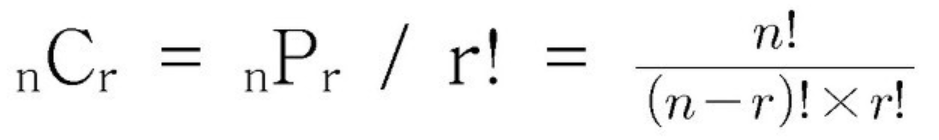
다음과 같이 구현 가능하다.
#include <iostream>
#include <vector>
using namespace std;
int n = 5, k=3, a[5] = {1,2,3,4,5};
void print(vector<int> &v){
for(int i : v) cout << i;
cout << endl;
}
void combination(int n , int k, int start , vector<int> &b){// 이렇게 계속 레퍼런스로 타고 들어가도 되는건가?
if(b.size() == k){
print(b);
return;
}
for(int i = start + 1; i < n ; i++){
b.push_back(a[i]);
combination(n,k, i, b);
b.pop_back();
}
return;
}
int main(){
vector<int> b;
combination(n, k, -1, b);
return 0;
}출력되는 순서를 고려해 보면
123 >> 124 >> 125 >> 134 >> 135 >> 145 >> 234 >> 235 >> 345 순으로 출력된다.
순열과 조합 모두 코딩 테스트에서 요긴하게 쓰일 수 있으니 기억해 두는 것이 좋다. 특히 순열을 재귀함수를 이용하여 구현하는 것은 로직이 복잡하니 자주 복기해주는 것이 좋을 것 같다.
