
실수 집합
All ordered n-tuples of real numbers(x1, x2, ..., xn)
Solution Set
선형 방정식의 solution set은 어떻게 보일 것인가?
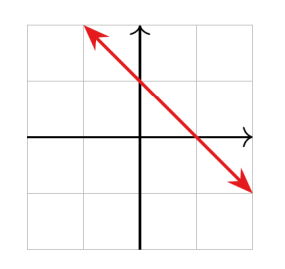
다음과 같이 시각화 할 수 있다. 위와 같은 식을 parametric form 으로 바꾸어 주면 아래와 같다
서로 다른 두개의 linear equation의 solution set은 어떻게 보일 것인가?
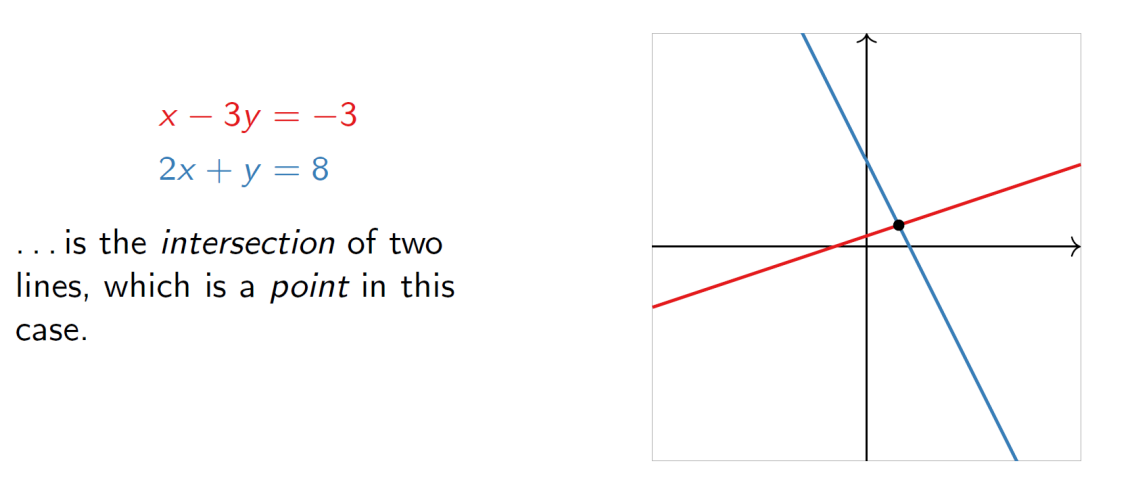
Solving System of Equations
- A solution is a list of numbers x,y,z,... that makes all of the equtaion true.
- The solution set is the collections of all solutions
- Solving the system means finding the solution set in a "parameterized" form
결국 solution이란 모든 방정식을 만족시키는 값을 의미하며, solution set이란 모든 sloution의 집합을 의미한다. System을 solving 한다는 것은 이러한 solution set을 parameterized 형태로 표현해주는 것이다.
그렇다면 어떻게 문제를 풀것인가 >> elementary row operation(기본 행 연산)을 활용한다.

기본 행 연산을 반복하여 아래와 같은 형태를 만들고 싶다.

이때 식을 간단하게 표현하기 위해 Augmented matrix 형태로 표현해서 계산을 진행하자.

Row Equivalence
위와 같이 식을 기본행연산을 이용하여 바꾸면 해가 달라지지는 않는가?
Row Equivalent : If one matrix can be obtained from the other by doing some number of elementary row operations, Two matrices are row equivalent
Row Equivalent 하다는 것은 기본 행 연산을 통해 동일한 형태로 만들수 있다는 것을 의미하며, Row Equivalent 한 경우 동일한 해를 가지게 된다.
따라서 기본 행 연산을 통해 식을 수정하더라도 우리는 해를 구할 수 있다.
Consistent, Inconsistent
해가 존재하면 Consistent, 존재하지 않으면 Inconsistent 하다고 한다.
