
Row Echelon Form
Solved matrix을 만든다고 가정할 때, 'Solved'를 어떻게 정의할 것인가? >> Row Echelon Form을 달성하면 Solved 되었다고 판단한다.
Row Echelon Form
1. All zero rows are at the bottom
2. Ecah leading nonzero entry of a row is to the right of the leading entry of the row above
- Below a leading entry of a row, all entries are zero
- 모두 0인 행은 가장 아래에 있어야 한다
- leading entry(처음으로 0 이 아닌 값이 나오는 원소)는 윗행의 leading entry 보다 오른쪽에 존재해야 한다.
- leading entry 아래의 모든 행의 원소들은 0이어야 한다.
그림으로 보면 아래와 같다
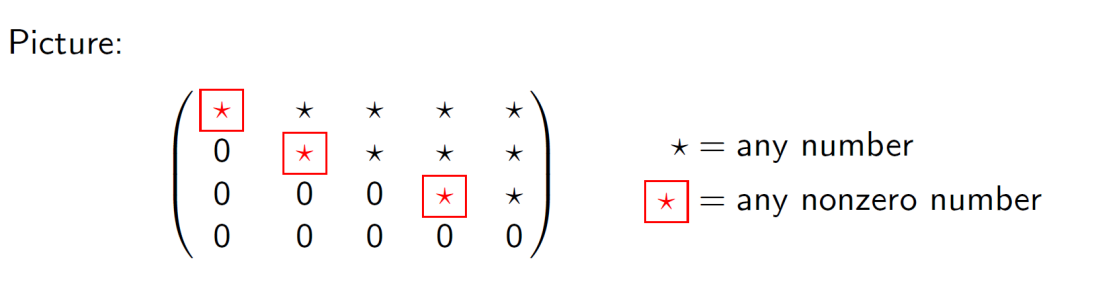
Pivot : The first nonzero entry of a row of a matrix
Pivot column : Column containing a pivot of a matrix in row echelon form
위에서 빨간 박스가 Pivot!
Reduced Row Echelon Form
Row Echelon Form에서 추가적으로 아래의 두 조건을 만족시키면 Reduced Row Echelon Form 이라 명명한다
Reduced Row Echelon Form
4. The pivot in each nonzero row is equal to 1.
5. Each pivot is the only nonzero entry in its columns
- Pivot 값이 1이고
- Pivot column은 pivot을 제외한 모든 값이 0 이어야 한다.
그림으로 보면 아래와 같다.

Row Reduction
모든 matrix는 하나의 RREF 을 가지고 있으며, 이는 Row equivalent 하다.
하나의 matrix를 RREF의 형태로 바꾸어 가는 과정을 row reduction 혹은 Gaussian Elimination이라고 한다.
Inconsistent Case
Augmented matix에서 마지막행의 마지막 행이 pivot column인 경우에만 Inconsistent 하다.

Summary

