AVL Tree

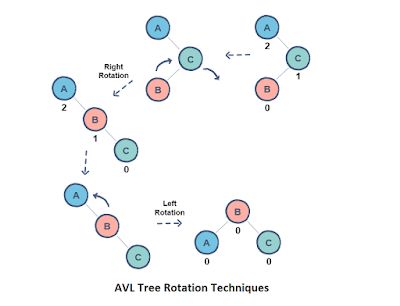
AVL Tree

Binary Search Tree에는 단점이 있음. Unbalanced하면 O(n)에 가까워 진다는 것
트리의 균형을 잡기위한 방법 중, AVL Tree는 하나의 방법
검색, 삽입, 삭제는 Binary Search Tree와 동일
다만, 삽입과 삭제시 트리의 균형을 검사하여 리벨런싱을 해주는 작업이 추가된 것
밸런싱 잡는데 엄격한 자료구조

Balance Factor

AVL Tree는 트리의 균형을 균형도(Balance Factor)으로 판단

Balance Facotr = Left Subtree Height - Right Subtree Height
이렇게 판단 했을 때,
-1,0,1 - Balanced
-2 <= Balance Factor <= 2 - Unbalanced -> Rebalancing

Types of Rebalancing

LL (Left-Left)

노드의 왼쪽 자식의 왼쪽에 값이 삽입되어 불균형이 발생한 경우
노드의 왼쪽 자식의 오른쪽에 값이 삭제되어 불균이 발생한 경우
(왼쪽 자식 노드에서 왼쪽 노드가 길게 늘어짐)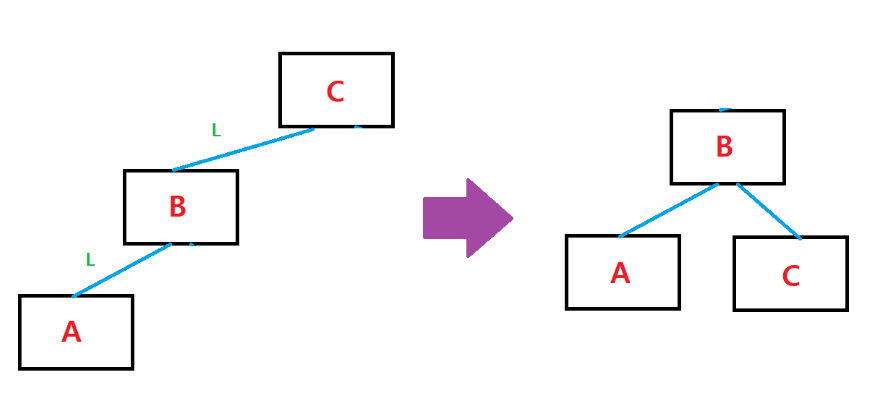

오른쪽으로 회전

RR (Right-Right)

노드의 오른쪽 자식의 오른쪽에 값이 삽입되어 불균형이 발생한 경우
노드의 오른쪽 자식의 왼쪽에 값이 삭제되어 불균형이 발생한 경우
(오른쪽 자식 노드에서 오른쪽 노드가 길게 늘어짐)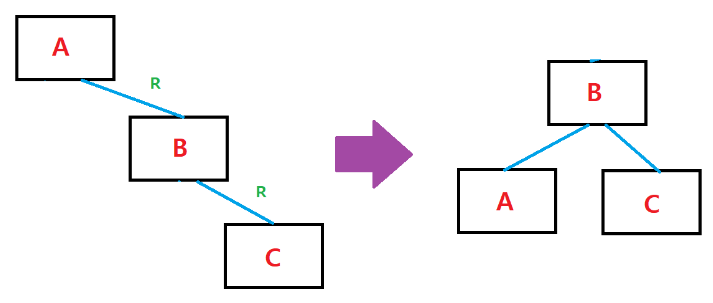

왼쪽으로 회전

LR (Left-Right)

노드의 왼쪽 자식의 오른쪽에 값이 삽입되어 불균형이 발생한 경우
노드의 왼쪽 자식의 왼쪽에 값이 삭제되어 불균형이 발생한 경우
(왼쪽 자식 노드에서 오른쪽 노드가 길게 늘어짐)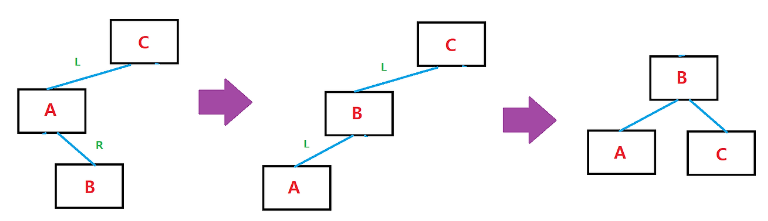

왼쪽 자식 노드에서 왼쪽으로 회전 후, 전체에서 오른쪽 회전

RL (Right-Left)

노드의 오른쪽 자식의 왼쪽에 값이 삽입되어 불균형이 발생한 경우
노드의 오른쪽 자식의 오른쪽에 값이 삭제되어 불균형이 발생한 경우
(오른쪽 자식 노드에서 왼쪽 노드가 길게 늘어짐)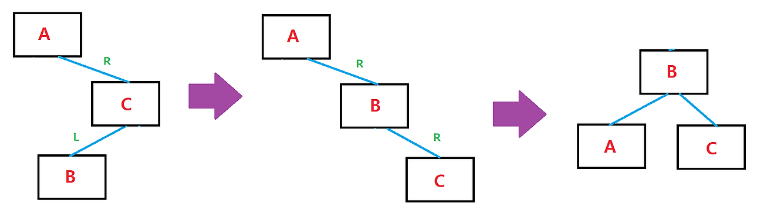

오른쪽 자식 노드에서 오른쪽으로 회전 후, 전체에서 왼쪽 회전

Implementation

#include<iostream>
#include<algorithm>
using namespace std;

struct Node {
    int  data;
    Node* left;
    Node* right;
    int height;     // 노드의 높이 정보 추가

    explicit Node(int value) : data(value), left(nullptr), right(nullptr), height(1) {}
};

class AVLTree {
private:
    Node* root;

    // AVL Tree 코드
    // 노드의 높이를 반환하는 함수
    int getHeight(Node* node) {
        if(node == nullptr) return 0;
        return node->height;
    }

    // 균형 인수를 계산하는 함수 (Left height - Right heigh)
    int getBalance(Node* node) {
        if(node == nullptr) return 0;
        return getHeight(node->left) - getHeight(node->right);
    }

    // LL
    Node* toRightRotate(Node* unbalancedNode) {
        // 왼쪽 자식 노드가 새로운 Root
        Node* newRoot = unbalancedNode->left;

        // 회전 수행 - B의 오른쪽을 A를 가리키고, A의 왼쪽은 nullptr을 가리킨다
        newRoot->right = unbalancedNode;
        unbalancedNode->left = nullptr;

        // 높이 정보 업데이트 - 하위 노드부터 업데이트
        unbalancedNode->height = max(getHeight(unbalancedNode->left), getHeight(unbalancedNode->right)) + 1;
        newRoot->height = max(getHeight(newRoot->left),getHeight(newRoot->right)) + 1;

        // 새로운 루트 반환
        return newRoot;
    }

    // RR
    Node* toLeftRotate(Node* unbalancedNode) {
        // 오른쪽 자식 노드가 새로운 Root
        Node* newRoot = unbalancedNode->right;

        // 회전 수행 - B의 왼쪽을 A를 가리키고, A의 오른쪽은 nullptr을 가리킴
        newRoot->left = unbalancedNode;
        unbalancedNode->right = nullptr;

        // 높이 정보 업데이트 - 하위 노드부터 업데이트
        unbalancedNode->height = max(getHeight(unbalancedNode->left), getHeight(unbalancedNode->right)) + 1;
        newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right)) + 1;

        // 새로운 루트 반환
        return newRoot;
    }


    // 삽입 함수 (재귀)
    Node* insert(Node* node, int value) {
        if(node == nullptr) {
            return new Node(value);
        }
        if(value < node->data) {
            node->left = insert(node->left, value);
        } else if(value > node->data) {
            node->right = insert(node->right, value);
        } else {
            return node;    // 중복된 값이면 반환 - insert를 진행하지 않겠다
        }

        // insert 후, 높이 업데이트
        node->height = 1 + max(getHeight(node->left), getHeight(node->right));

        // 균형 인수를 계산하여 트리가 불균형인지 확인
        int balanceFactor = getBalance(node);

        // 불균형 해결 : 균형 인수에 따라 네 가지 회전 경우
        if(balanceFactor > 1 && value < node->left->data) {
            // LL : 왼쪽 자식의 왼쪽에 새 노드가 추가된 경우
            return toRightRotate(node);
        }
        if(balanceFactor < -1 && value > node->right->data) {
            // RR : 오른쪽 자식의 오른쪽에 새 노드가 추가된 경우
            return toLeftRotate(node);
        }
        if(balanceFactor > 1 && value > node->left->data) {
            // LR : 왼쪽 자식의 오른쪽에 새 노드가 추가된 경우
            node->left = toLeftRotate(node->left);
            return toRightRotate(node);
        }
        if(balanceFactor < -1 && value < node->right->data) {
            // RL : 오른쪽 자식의 왼쪽에 새 노드가 추가된 경우
            node->right = toRightRotate(node->right);
            return toLeftRotate(node);
        }

        // 트리가 이미 균형이면 현재 노드 그대로 반환
        return node;
    }

    // 탐색 함수 (재귀)
    bool search(Node* node, int value) {
        if(node == nullptr) return false;
        if(node->data == value) return true;
        if(value < node->data) return search(node->left, value);
        return search(node->right, value);
    }

    // 삭제 함수 (재귀)
    Node* deleteNode(Node* node, int value) {
        if(node == nullptr) return nullptr;

        // 삭제할 값이 현재 노드의 값보다 작으면 왼쪽 서브트리에서 탐색
        if(value < node->data) {
            node->left = deleteNode(node->left, value);
        } else if(value > node->data) {     // 삭제할 값이 현재 노드의 값보다 크면 오르쪽 서브트리에서 탐색
            node->right = deleteNode(node->right, value);
        } else {
            // 자식이 없는 경우
            if(node->left == nullptr && node->right == nullptr) {
                delete node;
                return nullptr;
            } else if(node->left == nullptr) {  // 자식이 하나: 오른쪽 자식이 있는 경우
                Node* temp = node->right;
                delete node;
                return temp;
            } else if(node->right == nullptr) { // 자식이 하나: 왼쪽 자식이 있는 경우
                Node* temp = node->left;
                delete node;
                return temp;
            } else {    // 자식이 둘인 경우
                // 오른쪽 자식에서 가장 작은 노드 찾기
                Node* temp = findMin(node->right);
                // 그 찾은 노드의 값을 넣기
                node->data = temp->data;
                // 오른쪽 자식에서 그 찾은 노드를 삭제
                node->right  = deleteNode(node->right, temp->data);
            }
        }

        // 높이 정보 업데이트
        node->height = max(getHeight(node->left), getHeight(node->right));

        // 균형 인수 계산
        int balanceFactor = getBalance(node);

        // 불균형 해결 - 다른 if 조건문 사용
        if(balanceFactor > 1 && getBalance(node->left) > 0) {
            // LL
            return toRightRotate(node);
        }
        if(balanceFactor < -1 && getBalance(node->right) < 0) {
            // RR
            return toLeftRotate(node);
        }
        if(balanceFactor > 1 && getBalance(node->left) < 0) {
            // LR
            node->left = toLeftRotate(node->left);
            return toRightRotate(node);
        }
        if(balanceFactor < -1 && getBalance(node->right) > 0) {
            // RL
            node->right = toRightRotate(node->right);
            return toLeftRotate(node);
        }
        return node;    // 균형 상태면 그대로 반환
    }

    // 최솟값 찾기 (삭제 연산에서 사용)
    Node* findMin(Node* node) {
        while(node->left != nullptr) {
            node = node->left;
        }
        return node;
    }

    // 중위 순회 (In-order Traversal)
    void inorderTraversal(Node* node) {
        if(node == nullptr) return;
        inorderTraversal(node->left);
        cout<<node->data<<" ";
        inorderTraversal(node->right);
    }
public:
    // 생성자
    AVLTree() : root(nullptr){}

    // 삽입 함수
    void insert(int value) {
        root = insert(root, value);
    }

    // 탐색 함수
    bool search(int value) {
        return search(root, value);
    }

    // 삭제 함수
    void deleteNode(int value) {
        root = deleteNode(root, value);
    }

    // Inorder 출력
    void inorderTraversal() {
        inorderTraversal(root);
        cout<<endl;
    }
};

기존 Binary Search Tree에서 추가적으로 AVL Tree Balancing 코드를 작성
위 코드에서 LL, RR, LR, RL을 구분하는 방법이 두 가지가 있는데 논리적인 결과는 같다 (하나의 함수로 작성해서 Normalize해도 됨)

Efficiency

Linked List 기반 효율표

	AVL Tree	BST
삽입	O(log n)	O(n)
삭제	O(log n)	O(n)
탐색	O(log n)	O(n)
균형	항상 균형 유지	균형 유지 없음
최악	O(log n)	O(n)

Efficiency Summary

탐색이 빈번한 경우 효율적 (항상 균형을 유지하기 때문)
일관된 성능이 필요한 경우 효율적 (트리가 항상 균형)

삽입/삭제가 매우 빈번한 경우 비효율적 (회전 연산이 추가적인 연산 비용을 발생)
균형 유지가 불필요한 경우 (탐색보다 데이터의 단순 추가가 중요한 경우, 회전 연산은 불필요)

STL

AVL Tree를 사용하는 STL라이브러는 없음
Red-Blank Tree를 사용하는 STL은 많음