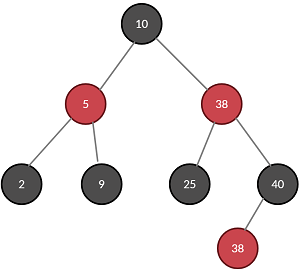
Red-Black Tree
Binary Search Tree의 한 종류, 자동으로 균형을 유지하게 보장하는 자료구조 중 한 종류
BST의 worst case의 단점을 개선, O(n)Properties
- 모든 노드는 Red or Black
- Root 노드는 Black
- 모든 nil 노드는 Black
nil 노드: 존재하지 않음을 의미하는 노드
RB 트리에서 leaf 노드는 nil 노드 - Red의 자녀들은 반드시 Black (Red가 연속적으로 존재할 수 없음)
- 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 Black 수는 같음 (자기 자신은 카운트 제외)
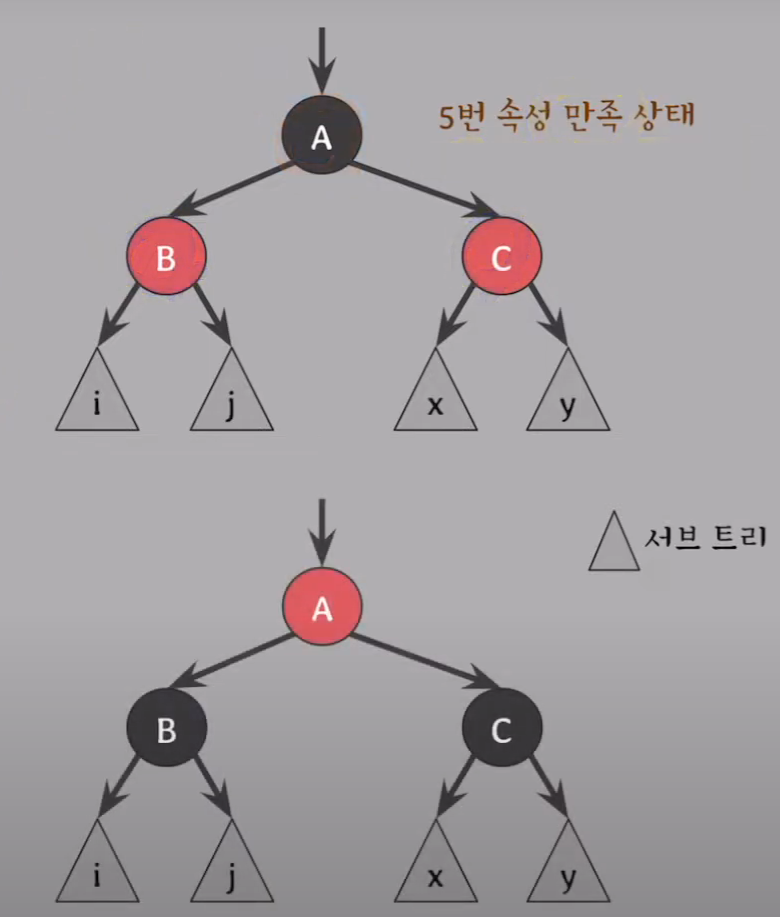
5번 속성 응용: RB 트리가 5번 속성을 만족할 때, 두 자녀가 같은 색을 가질 때 부모와 두 자녀의 색을 바꿔줘도 5번 속성은 여전히 만족한다
How to maintain balance
Red-Black 트리는 삽입/삭제 시 주로 #4/#5을 위반하며 이를 해결하기 위해 구조를 바꾸다 보면 자연스레 트리의 균현이 잡힘
Insertion
Overview
- 삽입 전 RB 트리 속성을 만족한 상태
- 삽입 방식은 일반적인 BST와 동일
- 삽입 후 RB 트리 위반 여부 확인
- RB 트리 속성을 위반했다면 재조정
- RB 트리 속성을 다시 만족
Insertion
삽입할 땐 항상 Red 노드
왜? 삽입 후에도 #5 속성을 만족하기 위해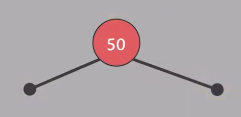
Insert(50) - 노드를 삽입할 때 Red, 두 nil 노드의 색은 Black으로 고정, #3 만족
#3 속성 위반
해결: Root 노드의 색을 Black으로 변환, 모든 속성 만족
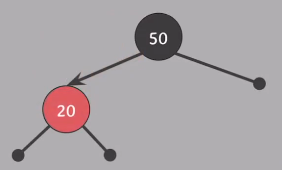
Insert(20), 모든 속성 만족
Case 3
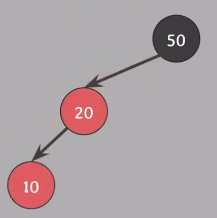
Insert(10), RB 트리의 #4 속성 위반
해결? Red 노드를 반대편으로 보낸다면? 단, 구조를 바꾼 후, BST 특징 또한 유지되어야 함
해결! 회전
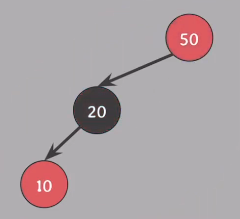
20과 50 노드의 색을 바꿈
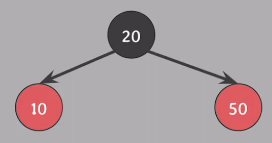
오른쪽으로 회전, 모든 속성 만족
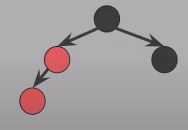
삽입된 Red 노드가 부모의 왼쪽 자녀 & 부모도 Red고 할아버지의 왼쪽 자녀 & 삼촌(=부모의 형제)은 Black이라면 부모와 할아버지의 색을 바꾼 후, 할아버지 기준으로 오른쪽으로 회전
반대 Case도 동일
Case 2
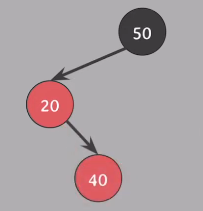
Insert(40), #4 속성 위반
해결? Case 3와 다른 점은 삽입된 노드를 기준으로 할아버지의 경로가 꺾였다는 점
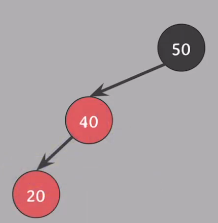
20 노드 기준으로 왼쪽으로 회전
Case 3 방식 사용
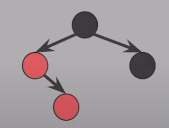
삽입된 Red 노드가 부모의 오른쪽 자녀 & 부모도 Red고 할아버지의 왼쪽 자녀 & 삼촌은 Black이라면 부모를 기준으로 왼쪽으로 회전한 뒤 Case 3의 방식으로 해결
반대 Case도 동일
Case 2
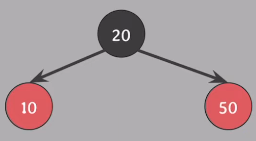
여기서 Insert(30)
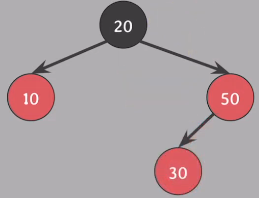
Insert(30)을 한 후, #4 속성 위반
Red가 한 쪽으로 몰려 있지 않아 Case 2를 사용 불가 (삼촌이 Black이 아님)
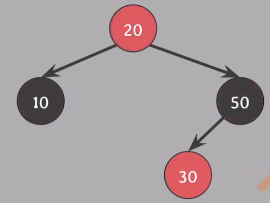
#5 속성 응용 활용, 여전히 #5 속성 성립
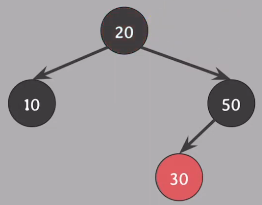
#2 속성 위반, Root 노드는 Black이기 때문에 Red에서 Black으로 변환
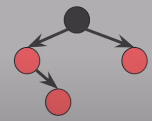
삽입된 Red 노드의 부모도 Red & 삼촌도 Red라면 부모와 삼촌을 Black으로 바꾸고 할아버지를 Red로 바꾼 뒤 할아버지에서 다시 확인을 시작함
Case 1은 Insert된 노드가 어디가 됬든 간에 Case 1을 사용
할아버지에서 다시 확인? 할아버지가 Root면 Black으로 바꾸면 되지만, 할아버지의 부모가 있다면 #4 속성을 위반하는지 확인해야됨
Example
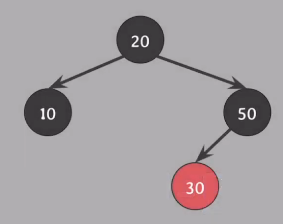
여기서 Insert(80)
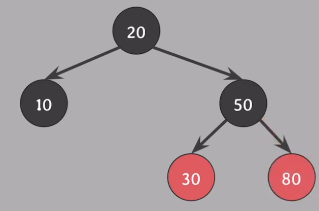
Red-Black 트리의 모든 속성 성립
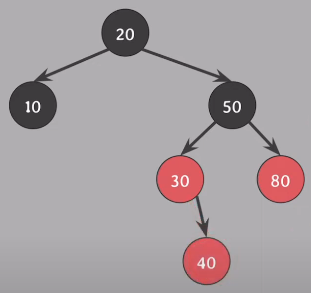
Insert(40), #4 속성 위반 - Case 1 상태 (부모 Red, 삼촌 Red)
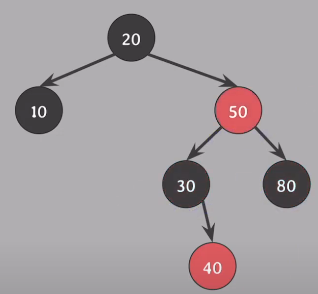
할아버지 - 부모, 삼촌 의 색 변경, 모든 속성 성립
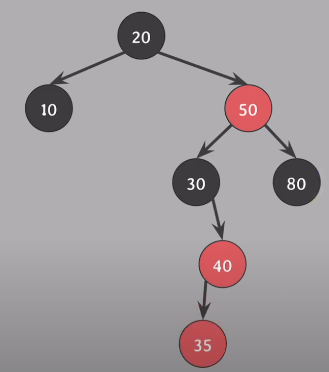
Insert(35), #4 속성 위반 - Case 2 상태 (자식은 부모의 왼쪽, 부모는 할아버지의 오른쪽)
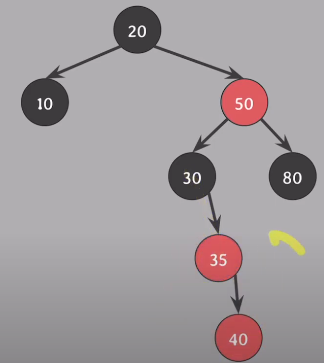
부모 기준으로 오르쪽으로 회전 - 이제 Case 3 상태
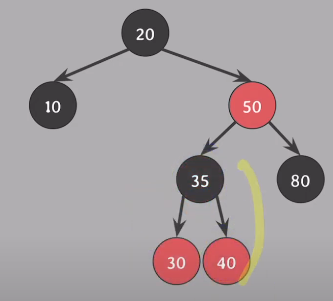
30과 35의 색상을 바꾸고 (30 Red, 35 Black), 할아버지 기준오로 왼쪽 회전
모든 속성 만족
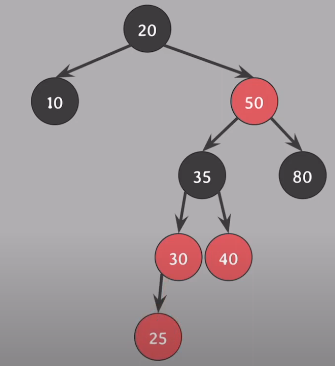
Insert(25), #4 속성 위반 - Case 1 상태
할아버지 - 부모, 삼촌 의 색상을 바꿈
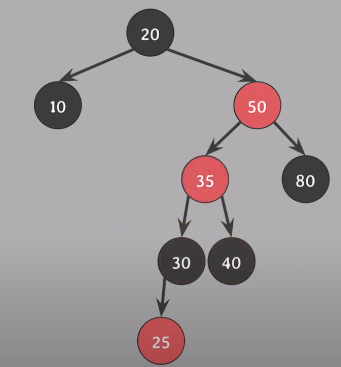
할아버지인 35에서 확인, #4 속성 위반 - Case 2 형태
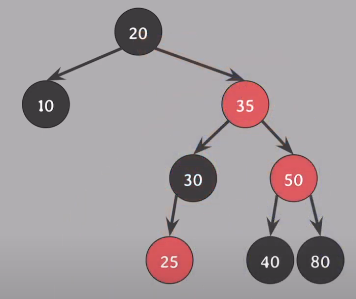
부모(50)를 기준으로 오른쪽 회전
35의 오른쪽 자식은 50이 되고, 40은 50의 왼쪽 자식으로 가게 됨
Case 3 상태
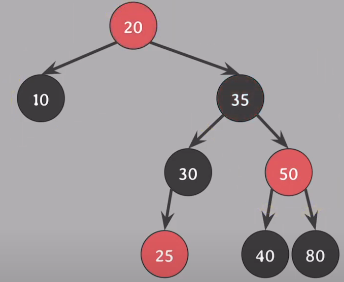
20과 35의 색을 바꿈
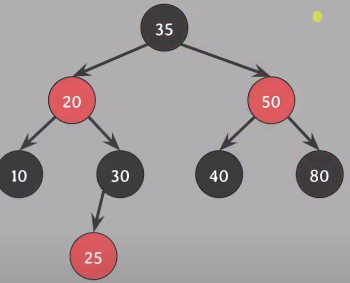
할아버지(20)기준으로 왼쪽으로 회전
35의 왼쪽 자식은 20이 되고, 20의 오른쪽 자식은 30이 됨
모든 속성 만족
