Graph

Graph?

그래프를 활용하여 복잡한 관계를 모델링하고 효율적인 알고리즘을 설계 가능
그래프는 정점(Vertext)와 간선(Edge)로 구성된 자료구조, 지하철 노선도처럼 여러 도시들(정점)이 노선(간선)으로 연결된 모습과 비슷

• Vertex: 데이터를 저장하는 노드
• Edge: 두 정점 사이의 연결 관계를 나타내는 선

Types of Graph

• 방향 그래프: 간선에 방향이 있는 그래프. 한쪽 방향으로만 이동 가능
• 무방향 그래프: 간선에 방향이 없는 그래프. 양쪽 방향으로 이동이 가능
• 가중치 그래프: 간선에 가중치(숫자)가 부여된 그래프. (가중치 - 거리, 비용, 시간 등)
• 비가중치 그래프: 모든 간선의 비용이 동일한 그래프

Type of expression

• 인접 행렬: 정점 간의 연결 관례를 2차원 배열로 표현하는 방법. 두 정점이 연결되어 있으면 해당 위치에 1을, 연결되어 있지 않으면 0
• 인접 리스트: 각 정점에 연결된 목록을 저정하는 방법. 각 정점을 하나의 리스트로 표현하고, 해당 리스트에 연결된 정점들을 저장

	장점	단점
인접 행렬	두 정점이 연결되어 있는지 확인하기 쉬움	간선이 적을 때 메모리를 많이 사용함
인접 리스트	간선이 적을 때 메모리 효율이 높음	두 정점이 연결되어 있는지 확인하기 위해 리스트를 순회해야 함

Traversal Graph

DFS, Depth-First Search

깊이 우선 탐색, 트리 탐색처럼 시작 정점에서 가능한 깊게 탐색
스택 or 재귀를 사용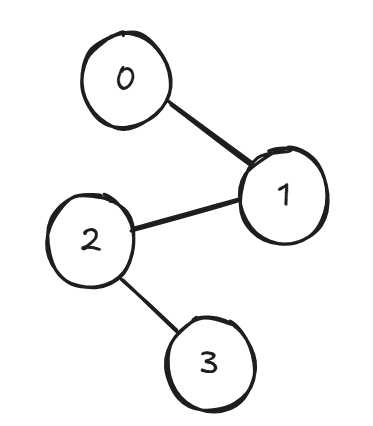

#include <iostream>
#include<vector>
using namespace std;

const int MAX = 5;

void DFS(int current, vector<int> graph[], bool visited[]) {
    visited[current] = true;
    cout<<current<<" ";

    for(int neighbor : graph[current]) {
        if(!visited[neighbor]) {
            DFS(neighbor, graph, visited);
        }
    }
}

int main() {
    vector<int> graph[MAX];
    bool visited[MAX] = {false};

    graph[0].push_back(1);
    graph[1].push_back(0);
    graph[1].push_back(2);
    graph[2].push_back(1);
    graph[2].push_back(3);
    graph[3].push_back(2);

    DFS(0,graph,visited);
    // Output: 0 1 2 3

    return 0;
}

방문한 노드를 먼저 visited를 true로 바꾸고, 출력 후, 더 깊게 들어간다(재귀 호출)
만약 3에서 더이상 호출할 노드가 없을 경우, 리턴
리턴 했는데 visited의 상태가 true면 바로 리턴

BFS, Breadth First Search

너비 우선 탐색, 시작 정점에서 가까운 정점부터 탐색
큐 자료구조 사용

#include <iostream>
#include<vector>
#include<queue>
using namespace std;

const int MAX = 5;

void BFS(int start, vector<int> graph[], bool visited[]) {
    queue<int> q;
    q.push(start);
    visited[start]=true;

    while(!q.empty()) {
        int current = q.front();
        q.pop();
        cout<<current<<" ";

        for(int neighbor : graph[current]) {
            if(!visited[neighbor]) {
                q.push(neighbor);
                visited[neighbor]=true;
            }
        }
    }

}

int main() {
    vector<int> graph[MAX];
    bool visited[MAX] = {false};

    graph[0].push_back(1);
    graph[1].push_back(0);
    graph[1].push_back(2);
    graph[2].push_back(1);
    graph[2].push_back(3);
    graph[3].push_back(2);

    BFS(0,graph,visited);
    // Output: 0 1 2 3

    return 0;
}

큐를 사용해서 현재 노드로부터 가까운 노드부터 탐색
큐가 Empty면 순회를 모두 했다는 뜻
현재 노드를 방문하면 visited를 true로 하고, 주변 노드를 찾아서(visited 안된 것만) 큐에 저장
이렇게 순회해서 큐에서 front를 하나씩 빼서 반목하면 너비 탐색

MST, Minimum Spanning Tree

최소 신장 트리, 가중치가 있는 연결 그래프에서 모든 정점을 연결하되, 간선의 가중치 합이 최소가 되는 트리

Spanning Tree = 신장 트리 = 최소 연결 트리 = 간선의 수가 가장 적다

MST의 특징

1. 간선의 가중치의 합이 최소여야 함
2. n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용해야 함
3. 사이클이 없어야 하고, 있을 수 없음

MST의 구현 방법

1. Kruskal MST Algorithm

탐욕적인 방법(Greedy)를 이용하여 모든 정장을 최소 비용을 연결하는 최적 해답을 구하는 것

방법

• MST가 최소 비용의 간선으로 구성 됨
• 사이클을 포함하지 않음의 조건에 근거하여 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택

과정
1. 그래프의 간선들을 가중치의 오름차순으로 정렬
2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택 (가장 낮은 가중치를 먼저 선택, 사이클을 형성하는 간선을 제외)
3. 해당 간선을 현재의 MST의 집합에 추가

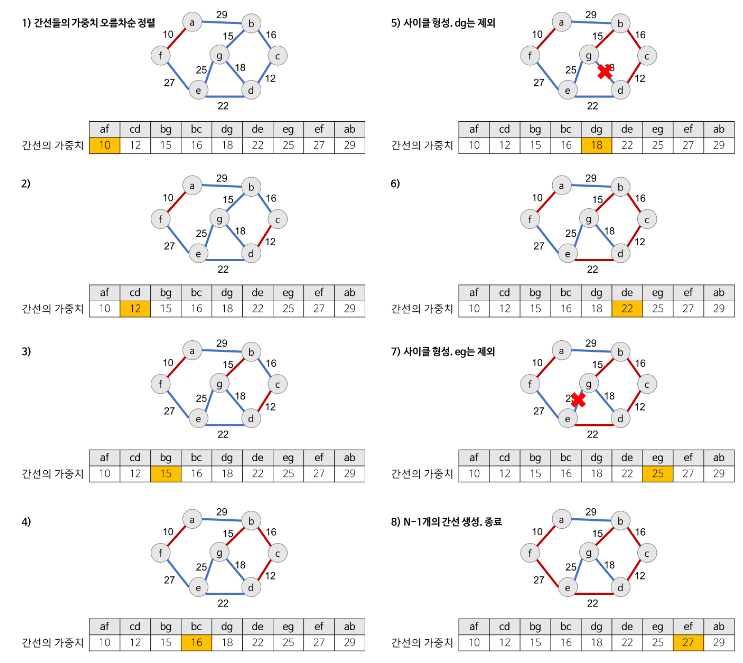
참고: https://gmlwjd9405.github.io/2018/08/29/algorithm-kruskal-mst.html

2. Prim MST Algorithm

시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장 해나가는 방법

방법

• 정점 선택을 기반으로 하는 알고리즘
• 이전 단계에서 만들어진 신장 트리를 확장하는 방법

과정
1. 시작 단계에서 시작 정점만이 MST 집합에 포함
2. 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장 (가장 낮은 가중치를 먼저 선택)
3. 위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복

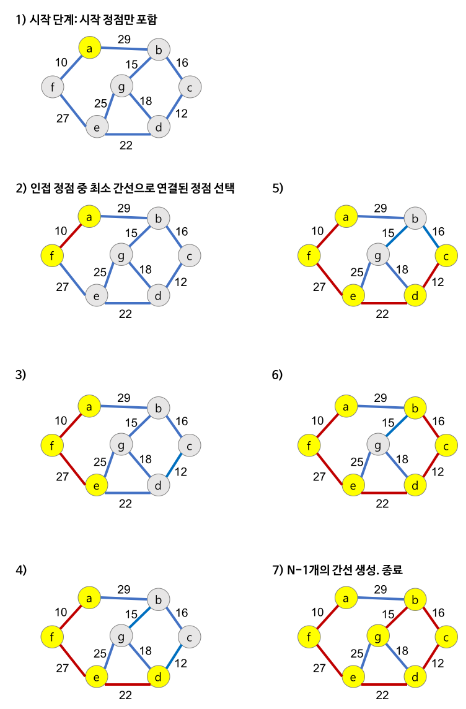
참고: https://gmlwjd9405.github.io/2018/08/30/algorithm-prim-mst.html#google_vignette

최단 경로 알고리즘

그래프에서 최단 경로란 시작 노드에서 도착 노드까지의 최단 경로를 의미
거리가 짧다의 의미는 
비가중치 그래프는 경로 상에 있는 간선의 수가 적을 수록 거리가 짧은 것이고
가중치 그래프는 경로 상에 있는 간선의 가중치 합이 작을 수록 거리가 짧은 것이다

종류

1. 다익스트라 알고리즘
2. 벨만-포드 알고리즘
3. 플로이드-워셜 알고리즘