Deletion
Overview
- 삭제 전 RB 트리 속성 만족한 상태
- 삭제 방식은 일반적인 BST 동일
- 삭제 후 RB 트리 속성 위반 여부 확인
- RB 트리 속성을 위반했다면 재조정
- RB 트리 속성을 다시 만족
속성 위반 여부 확인
RB 트리에서 노드를 삭제할 때 어떤 색이 삭제되는지가 속성 위반 여부를 확인할 때 매우 중요
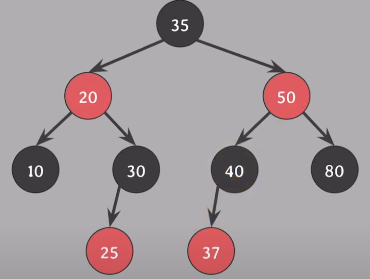
삭제하려는 노드의 자녀가 없거나 하나라면
삭제되는 색 = 삭제되는 노드의 색
37삭제 >> Red 노드 삭제
80삭제 >> Black 노드 삭제
40삭제 >> Black 노드 삭제
삭제하려는 노드의 자녀가 둘이라면
삭제되는 색 = 삭제되는 노드의 successor의 색
successor: 삭제되는 노드의 대체자
20삭제 >> successor 25 >> Red 삭제
35삭제 >> successor 37 >> Red 삭제
50삭제 >> successor 80 >> Black 삭제
그럼 삭제되는 색이 Red라면 어떠한 속성도 위반하지 않음
삭제되는 색이 Black이라면 #2, #3, #4을 위반 가능
위반 해결
삭제되는 색이 Black일 때 특수한 상황을 제외하면 #5속성을 항상 위반하게 됨
삭제되는 색이 Black이고 #5 위반일 때 extra black 부여 - #5속성을 다시 만족시키기 위해 삭제된 색의 위치를 대체한 노드에 Extra Black을 부여
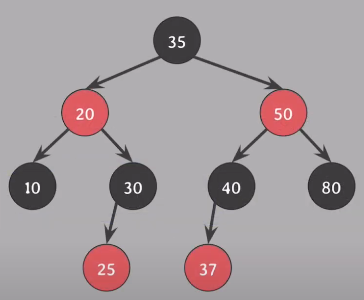
10노드 삭제 - 자녀 없음, 삭제되는 색 Black
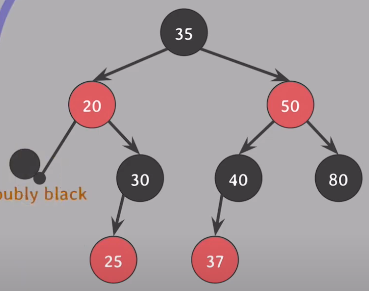
삭제된 위치에 nil노드가 대체, 여기에 Extra Black 부여 (Doubly Black)
#5속성 만족
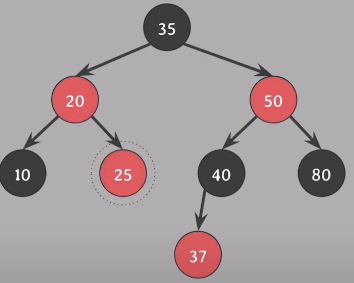
기존 트리에서 30을 삭제 - #5속성 위반
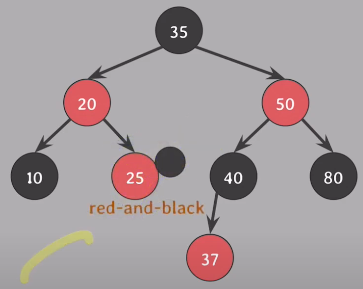
삭제된 위치에 대체자에게 extra black을 부여
25노드에 부여 (red-and-black)
#5속성 다시 만족
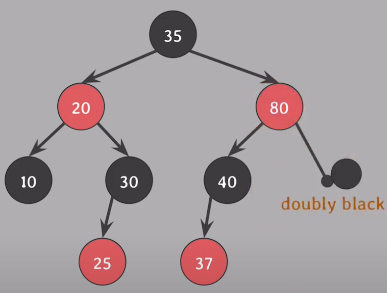
기존 트리에서 50을 삭제 - 자식 노드가 2개이기 때문에 successor인 80이 색을 물려받고, 삭제된 색은 Black임
삭제되고 대체된 곳에 extra black부여, nil노드에 부여 (doubly black)
#5속성 만족
red-and-black 해결
red-and-black을 black으로 바꾸면 해결
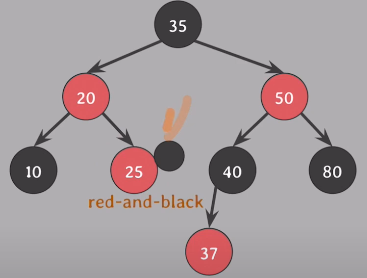
기존 트리에서 30노드를 삭제하고 자식이 하나이기 때문에 대체자로 25가 오고, #5속성을 만족하기 위해 extra black을 부여하면 위 그림처럼 red-and-black이 나옴
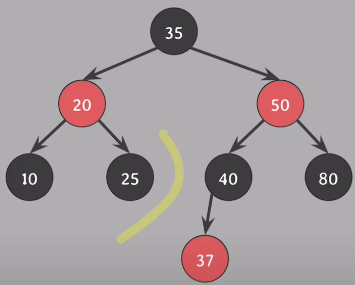
red-and-black이 됬으니 black으로 바꿔주면 해결, 모든 속성 만족
doubly black 해결
doubly black의 extra black을 없애는 방법은 총 4가지 case로 분류됨
Case 4
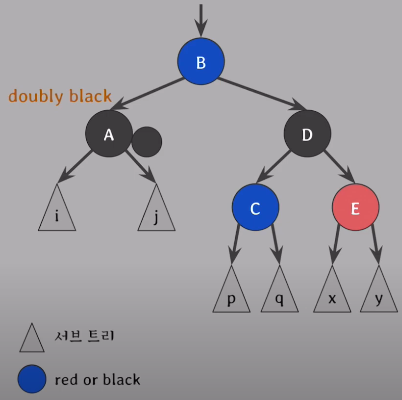
doubly black의 오른쪽 형제가 black & 형제의 오른쪽 자녀가 red일 때
그 red를 doubly black의 위로 옮기고 옮긴 red로 extra black을 전달해서 red-and-black으로 만들면 red-and-black을 black으로 바꿔서 해결
그럼 red를 왼쪽으로 보내기 위해서는 D의 위치가 먼저 Red가 되어야 함
#5속성의 응용을 사용해 보자
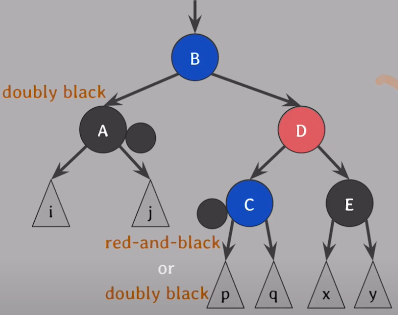
부모와 자식들의 색을 바꿔도 #5속성은 성립한다
D를 red로 바꾸고, 각 C,E는 Black을 부여한다
C: red-and-black / doubly black
E: Black
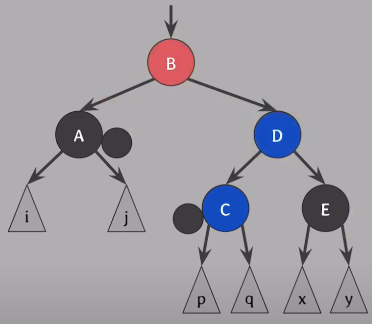
red가 왼쪽으로 넘어갈 수 있도록 왼쪽으로 회전 전에 B와 D의 색을 바꿈
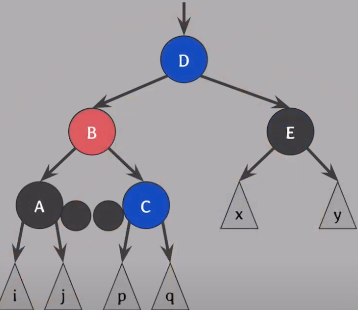
B를 기준으로 왼쪽으로 회전
B는 D의 왼쪽 자식이 되고, C는 붕뜨니 B의 오른쪽 자식이 됨
여전히 #5속성 만족
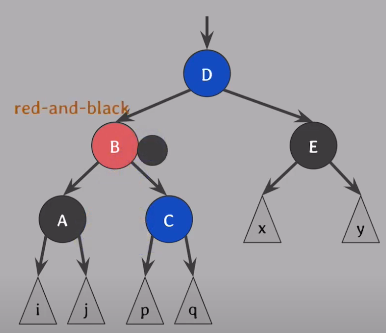
각 자식에 있던 extra black을 부모인 B에 extra black으로 합쳐줌 (각 자식의 각 하나의 extra black을 부모로 옮기기 때문에 속성을 여전히 만족)
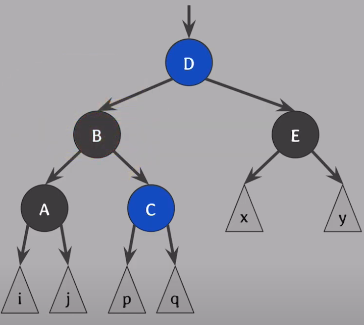
red-and-black을 black으로 바꿔줌
결과론적으로 오른쪽 형제(D)는 부모의 색(B)으로, 오른쪽 형제의 오른쪽의 오른쪽 자녀(E)는 Black으로, 부모(B)는 Black으로 바꾼 후, 부모(B)를 기준으로 왼쪽으로 회전하면 해결
Case 3
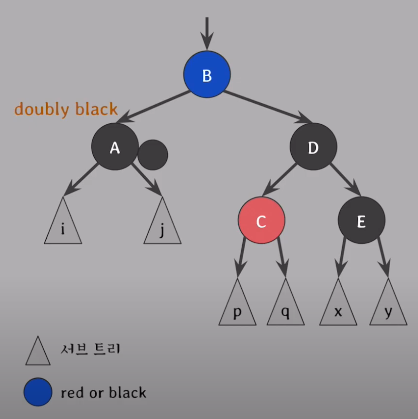
doubly black의 오른쪽 형제가 Black & 형제의 왼쪽 자녀가 Red & 그 형제의 오른쪽 자녀는 Black
doubly black의 형제의 오른쪽 자녀가 red가 되게 만들어 이후엔 Case 4을 적용하여 해결
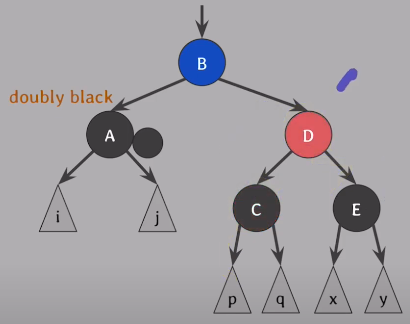
E위치에 red가 오도록 만들기 위해 C와 D의 색을 바꿈
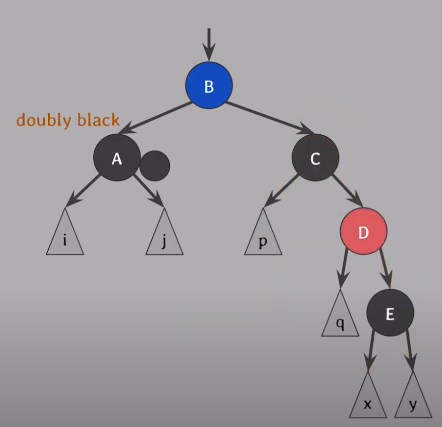
D를 기준으로 오른쪽으로 회전
C의 오른쪽 자식은 D, D의 왼쪽 자식은 C의 오른쪽자식으로 대체
이제 Case 4와 같음
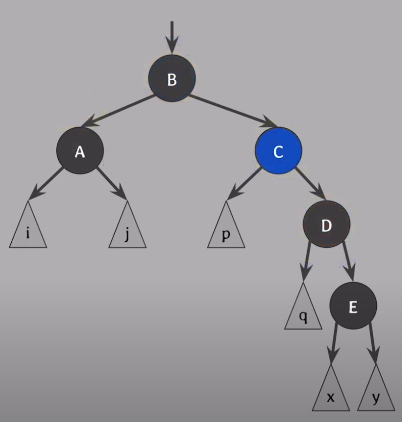
C는 부모의 색(B)인 red or black으로 바꾸고, D는 Black, B는 Black으로 바꿈
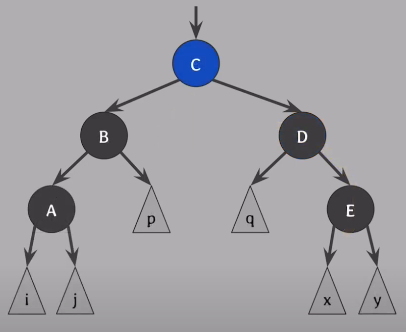
B기준으로 왼쪽으로 회전 시키면 해결
C의 왼쪽 자식은 B가 되고, B의 오른쪽 자식은 C의 왼쪽 자식으로 대체 됨
결과론적으로 Case 3의 트리를 Case 4형태로 바꾼 뒤(doubly black의 형제의 오른쪽 자녀를 red가 되게), Case 4를 사용해 해결
Case 2
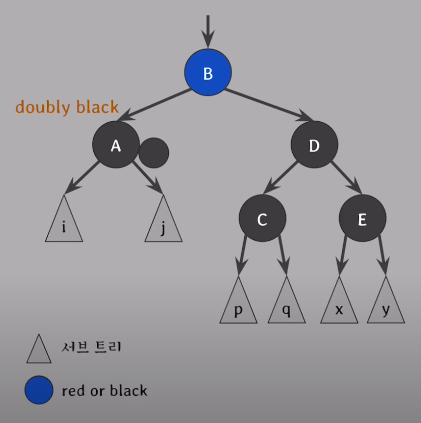
doubly black과 그 형제가 black & 형제의 두 자녀 모두 black일 때
doubly black과 그 형제의 black을 모아서 부모에게 전달해 부모가 extra black을 해결하도록 함
A와 A의 형제 D의 black을 모아서 A와 D에서 black을 모았기 때문에 A는 여전히 black이고 D는 red가 됨
black을 전달받은 B는 red-and-black 혹은 doubly black이 됨, 여전히 #5속성은 만족
B가 red-and-black이면 black으로 바꾸고 상황 종료
B가 doubly black이면 B가 Root노드면 black으로 바꿔서 해결, 아니면 Case 1,2,3,4중에 하나로 해결
Case 1
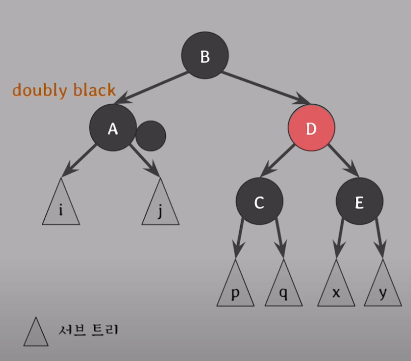
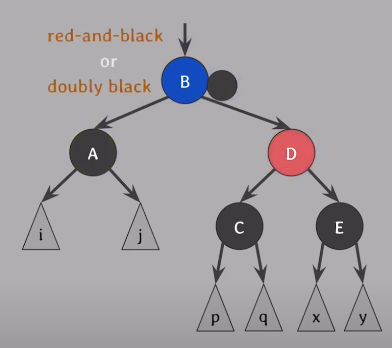
doubly black의 형제가 red일때
doubly black의 형제를 black으로 만든 후, Case 2,3,4 중에 하나로 해결
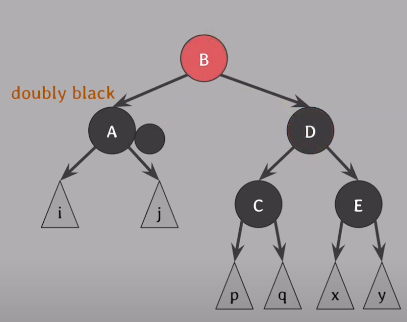
회전 후에도 #5속성을 만족하려면 B와 D의 색을 먼저 바꿔줌
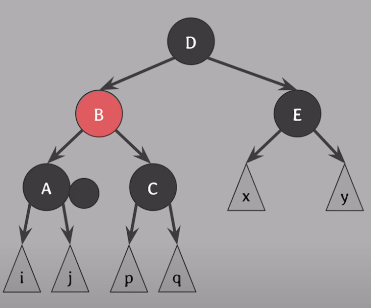
B기준으로 왼쪽으로 회전
회전 후, doubly black의 형제가 black이 되었기 때문에 Case 2,3,4중에 사용해서 해결
Example
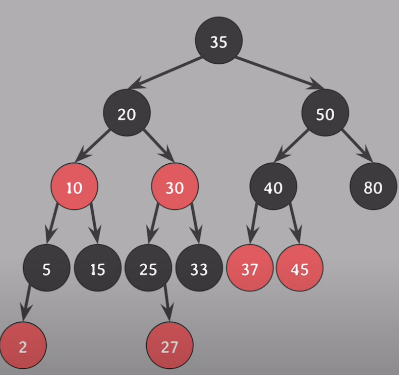
delete(15) - 삭제되는 노드 15, 삭제되는 색은 15의 black, 15d위치를 대체할 nil에 extra black을 부여
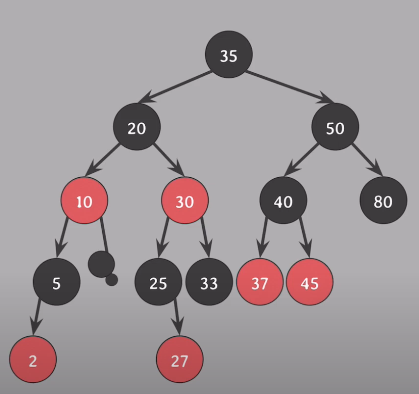
doubly black 형제가 black이고(Case 2,3,4), 형제의 왼쪽 자식이 red이니 - Case 4로 해결
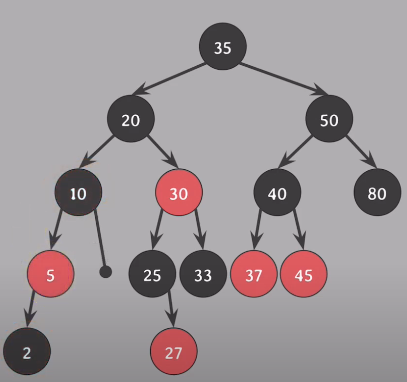
5는 부모노드의 색을 따라가고 - red
2, 10은 black으로 바꾼다
nil의 doubly black은 제거
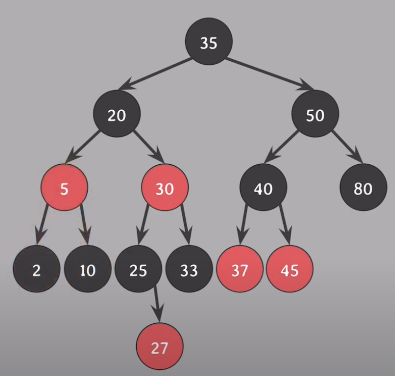
10을 기준으로 오른쪽 회전
모든 속성을 만족
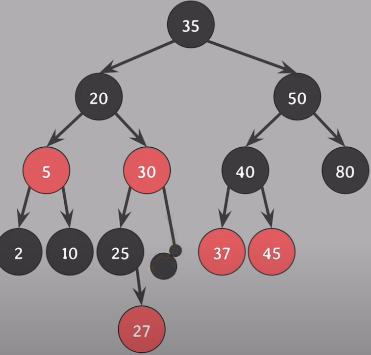
delete(33) - 삭제되는 노드 33, 삭제되는 색은 black, 대체할 노드인 nil에 extra black을 부여 (doubly black)
extra black 해결: doubly black의 형제가 black (Case 2,3,4중 하나), 형제의 오른쪽 노드 red - Case 3
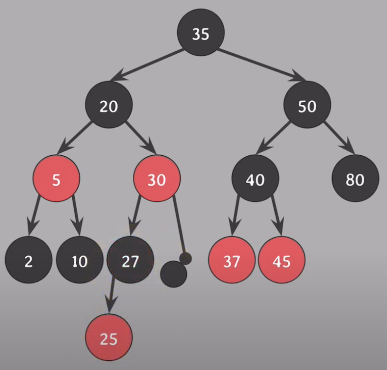
Case 3는 Case 4를 활용하기 위해 red를 형제의 왼쪽 자식으로 옮겨줘야한다
먼저 25와 27의 색을 바꾼 후 (25 red, 27 black), 25기준 왼쪽으로 회전 - Case 4 형태
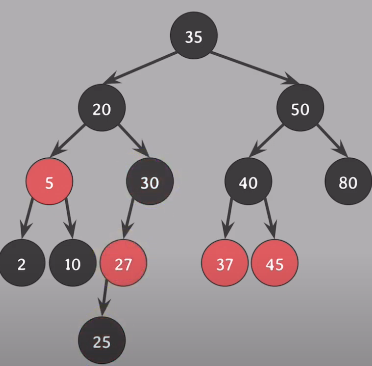
회전하기 전, 색 변경 형제인 27은 부모의 색 red로 바꾸고, 부모, 형제의 왼쪽 자식 (30,25)는 black
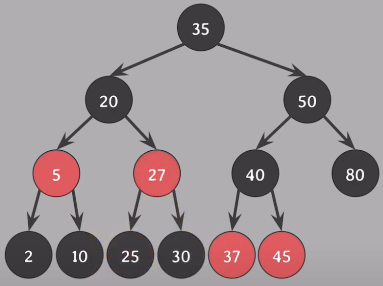
30기준으로 오른쪽 회전 - 모든 속성 성립
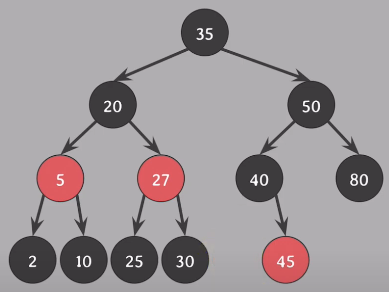
delete(37) - 삭제되는 노드 37, 삭제되는 색 red, 바로 상황 종료
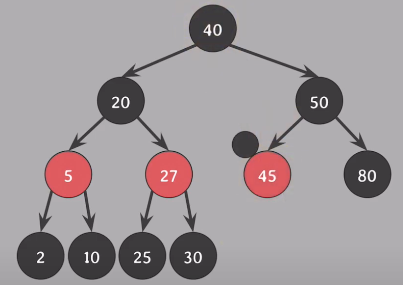
delete(35) - 삭제되는 노드 35, 삭제되는 색은 40(35의 successor)의 black, 40의 위치를 대체할 45(40의 successor에 extra black을 부여
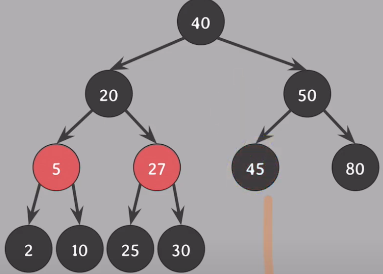
45가 red-and-black이기 때문에 black으로 바꾸고 상황종료 - 모든 속성 만족
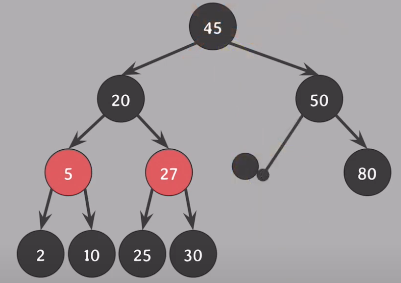
delete(40) - 삭제되는 노드 40, 삭제되는 색 45(40의 successor) black, 45위치를 대체할 nil노드에 extra black 부여
nil노드가 doubly black 해소
형제 노드 black(Case 2,3,4), 형제의 두 자식 모두 black - Case 2
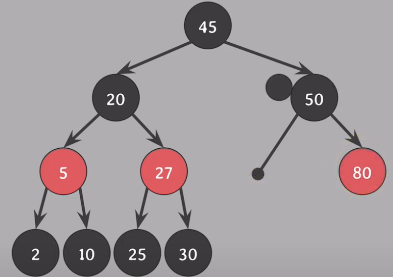
nil노드의 extra black과 80의 black을 부모로 올린다
50의 doubly black을 해소
형제 black (Case 2,3,4), 왼쪽 자식 red - Case 4 사용
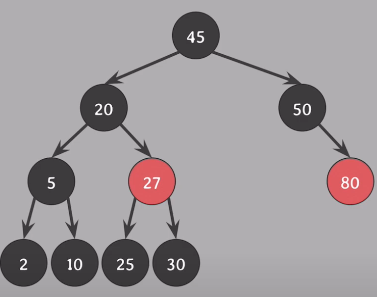
형제는 부모 색 - black
부모, 형제의 왼쪽 자식 - black
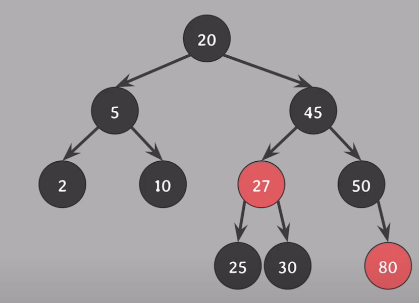
45를 기준 오른쪽으로 회전
20이 Root가 되고, 20의 오른쪽 자식 45
45의 왼쪽 자식은 20의 오른쪽 자식이였던게 붙음
모든 속성 만족
Red-Black Tree Time Complexity
| average | worst | |
|---|---|---|
| Insert | O(log n) | O(log n) |
| Delete | O(log n) | O(log n) |
| Search | O(log n) | O(log n) |
AVL vs Red-Black Tree
| AVL | Red-Black Tree | |
|---|---|---|
| 삽입/삭제/검색 시간복잡도 | 모두 O(log n) | 모두 O(log n) |
| 삽입/삭제 성능 | RB트리에 비해 느림 | AVL보다 빠름 |
| 검색 성능 | RB트리에 비해 빠름 | AVL 트리에 비해 느림 |
| 균형 잡는 방식 | balance factor가 (-1,0,1)가 되도록 | red-black 속성을 만족하도록 |
