Stack
Last In, First Out인 후입선출 구조를 가진 자료구조
Implementation
Linked List를 사용한 Stack 구현
#include<iostream>
using namespace std;
struct Node {
int data;
Node* next;
explicit Node(int value) : data(value), next(nullptr){}
};
class Stack {
private:
Node* topNode;
public:
explicit Stack() : topNode(nullptr){}
void push(int value) {
Node* newNode = new Node(value);
newNode->next = topNode;
topNode = newNode;
}
void pop() {
if(empty()) return;
Node* temp = topNode;
topNode = topNode->next;
delete temp;
}
int top() const {
if(empty()) return -1;
return topNode->data;
}
bool empty() const {
return topNode == nullptr;
}
int size() const {
int count = 0;
Node* cur = topNode;
while(cur != nullptr) {
count++;
cur = cur->next;
}
return count;
}
~Stack() {
while(!empty()) {
pop();
}
}
};
int main() {
Stack stack;
stack.push(10);
stack.push(20);
stack.push(30);
cout<<"Top element: "<<stack.top()<<endl;
stack.pop();
cout<<"Top element: "<<stack.top()<<endl;
cout<<"Stack size: "<<stack.size()<<endl;
if(stack.empty()) {
cout<<"Stack is empty"<<endl;
}else {
cout<<"Stack is not empty"<<endl;
}
return EXIT_SUCCESS;
}
Output
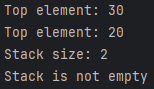
Efficiency
Linked List 기반 스택 효율표
| Time Complexity | Explaination |
|---|
| Search | O(1) | 스택의 top 노드만 접근 가능하므로 상수 시간, O(1) |
| Insertion | O(1) | 새로운 노드를 추가하고 top 노드만 수정하면 되므로 상수 시간, O(1) |
| Deletion | O(1) | top 노드만 제거하고 이전 노드로 이동하면 되므로 상수 시간, O(1) |
Efficiency Summary
마지막으로 추가된 데이터만 처리할 때, LIFO 구조가 필요할 때 적합
임의의 인덱스에 접근해야 하는 경우 부적합
중간에 데이터를 삽입하거나 삭제해야 하는 경우 부적합
데이터 정렬이 필요한 경우 부적합
STL
std::stack
스택의 동작을 제공하는 클래스 자료구조
실제 자료구조는 std::deque를 기본으로 함


