[WIL] Jungle 5주차 Red-Black Tree 레드 블랙 트리 요점 정리와 코드 작성(C)

@developer/takealittle.time·2024년 10월 14일

Jungle

목록 보기

12/21

✅ 이번 주차 학습을 진행하며 어려웠던 점

머릿속에 어떠한 개념론에 대해 순서를 가지고 스토리 라인을 그려 이해하는 편인데, Red-Black Tree 같은 경우 삭제 연산에 대한 스토리 라인이 머릿속에 잘 들어오지 않았다.

삭제 연산에서는 Extra-Black 개념을 쓰기 시작하면서 화려한 설명을 듣다보니, 나중에는 삽입 연산과 삭제 연산이 머릿속에서 아예 따로 놀기 시작했다.
(심지어 Extra-Black에 대한 설명도 참고하는 자료에 따라 설명이 다 다르거나 없었다.)

→ 이에 대해 얻은 인사이트를 공유하고자 한다.

7기 정글러이자 든든한 나의 룸메이트, 재명이형님께 감사를 전하며. 😊

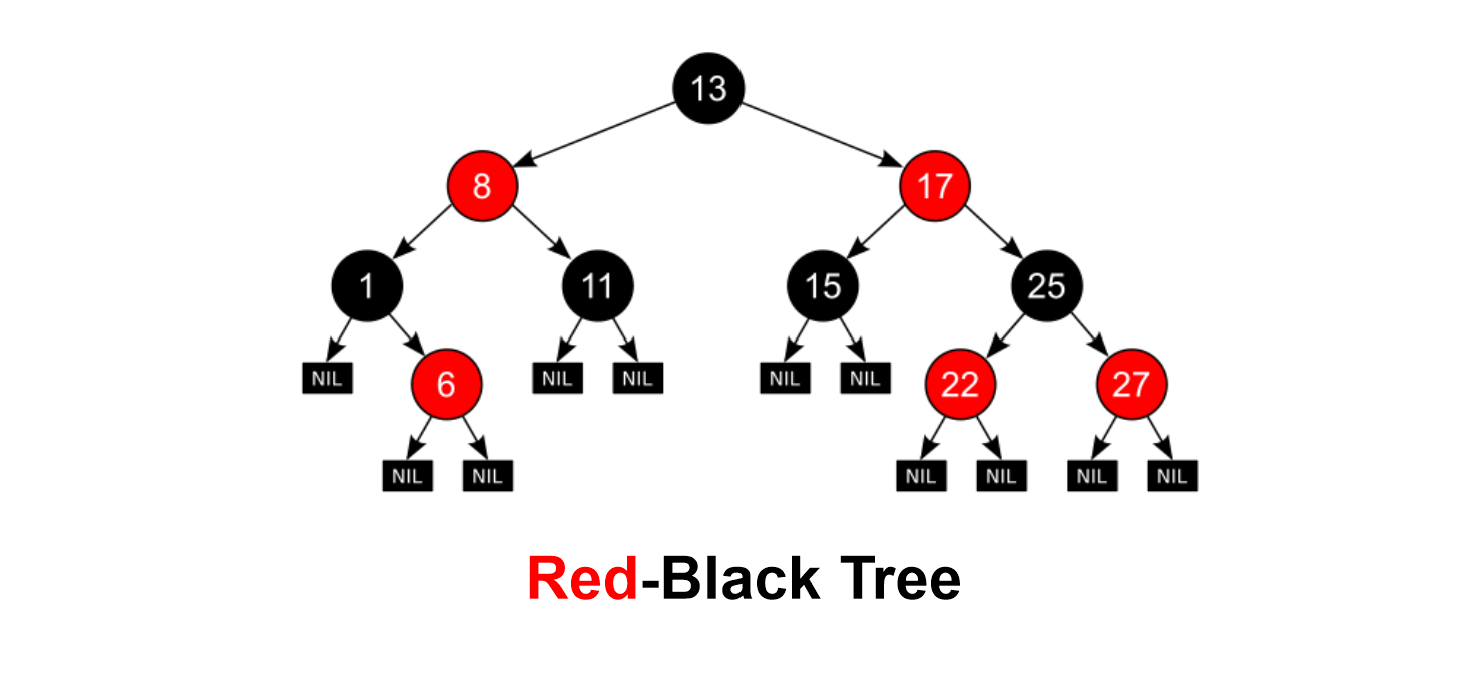
< Red-Black Tree >

BST (Binary Search Tree)의 한 종류.
스스로 균형을 잡는 트리.
BST의 worst case를 개선. O(N) -> O(logN)

01. RB-tree의 속성

RB-tree의 속성.

#1. 모든 노드는 Red 혹은 Black의 색상 속성을 가진다.

#2. 루트 노드는 Black 색상을 속성으로 가진다.

#3. 모든 nil 노드는 Black이다.

#4. Red의 자녀들은 항상 Black 색상을 속성으로 가진다.
( = Red는 연속적으로 존재할 수 없다!)

#5. 노드 x에서 임의의 자손 nil 노드까지 내려가는 경로에서 자기 자신을 제외한 Black의 수 (Black height)는 같다.

** RB트리가 #5 속성을 만족하고 있고, 두 자녀가 같은 색을 가질 때, (부모의 색) ↔ (두 자녀의 색)을 바꿔줘도 #5 속성은 여전히 만족한다.

02. RB-Tree가 균형을 잡는 방법?

삽입 / 삭제 시 주로 #4, #5를 위반 → 이를 해결하며 구조를 수정하다보면 → 자연스럽게 균형이 잡힌다.

들어가기 전에.

코드 작성 :: 필요한 구조체 등 선언

#ifndef _RBTREE_H_
#define _RBTREE_H_

#include <stddef.h>

typedef enum { RBTREE_RED, RBTREE_BLACK } color_t;

typedef int key_t;

typedef struct node_t {
  color_t color;
  key_t key;
  struct node_t *parent, *left, *right;
} node_t;

typedef struct {
  node_t *root;
  node_t *nil;  // for sentinel
} rbtree;

코드 작성 :: 트리 초기화 함수, 삭제 함수

rbtree *new_rbtree(void) {
  // make new rbtree
  rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
  // if rbtree is created, initialize its root node and nil node.
  if (p != NULL)
  {
    p->nil = (node_t*)calloc(1,sizeof(node_t));
    p->nil->color = RBTREE_BLACK;
    p->root = p->nil;
  }
  // return rbtree
  return p;
}


void delete_rbtree_nodes(node_t *node, node_t *nil) {
  if (node != nil) {
    // reclame left child, right child, and then current node.
    delete_rbtree_nodes(node->left, nil); 
    delete_rbtree_nodes(node->right, nil);
    free(node);
  }
}

void delete_rbtree(rbtree *t) {
  if (t != NULL) {
    // reclaim all node of tree recursively
    delete_rbtree_nodes(t->root, t->nil);  // 트리의 모든 노드 해제
    // reclaim sentinel node, and root node
    free(t->nil); 
    free(t);
  }
}

회전 C 코드

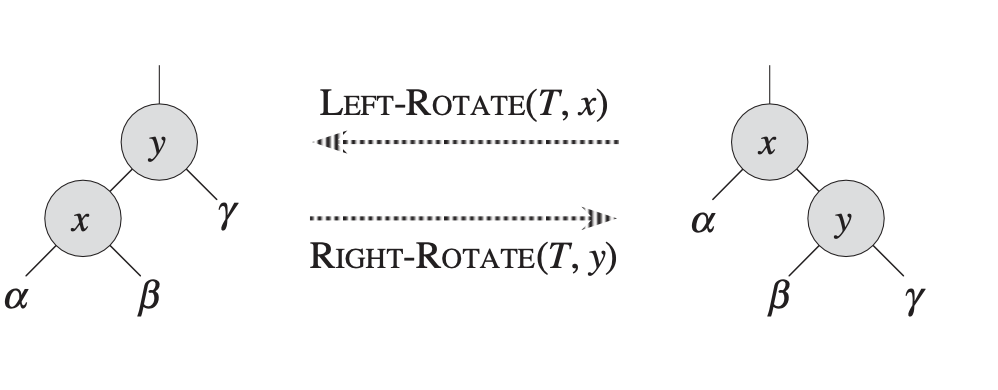
왼쪽 회전

void left_rotate(rbtree* t, node_t* x){
  node_t* y = x->right;
  // rotate left subtree of y to right subtree
  x->right = y->left;
  // if left subtree of y isn't vacant, x will be parent of subtree
  if (y->left != t->nil){
    y->left->parent = x;
  }
  // parent of x will be parent of y
  y->parent = x->parent;
  // if x is root node, y will be root node
  if (x->parent == t->nil)
    t->root =y;
  // if x is left child, y will be left child
  else if (x == x->parent->left)
    x->parent->left = y;
  // if x is right child, y will be right child
  else
    x->parent->right = y;
  // x will be left child of y
  y->left = x;
  x->parent = y;
}

오른쪽 회전

// reverse of left_rotate
void right_rotate(rbtree* t, node_t* y){
  node_t* x = y->left;
  y->left = x->right;
  if (x->right != t->nil){
    x->right->parent = y;
  }
  x->parent = y->parent;
  if (y->parent == t->nil)
    t->root = x;
  else if (y == y->parent->right)
    y->parent->right = x;
  else
    y->parent->left = x;
  x->right = y;
  y->parent = x;
}

<RB-Tree의 삽입과 삭제에 앞서>

* '균형을 맞춘다'는 아이디어 🔍

다음과 같이 [ 3, 5, 7, 16, 22, 26, 30 ] 7개의 노드를 가지고 있는 두 개의 트리에서 '3'을 검색하는 상황을 가정해보자.
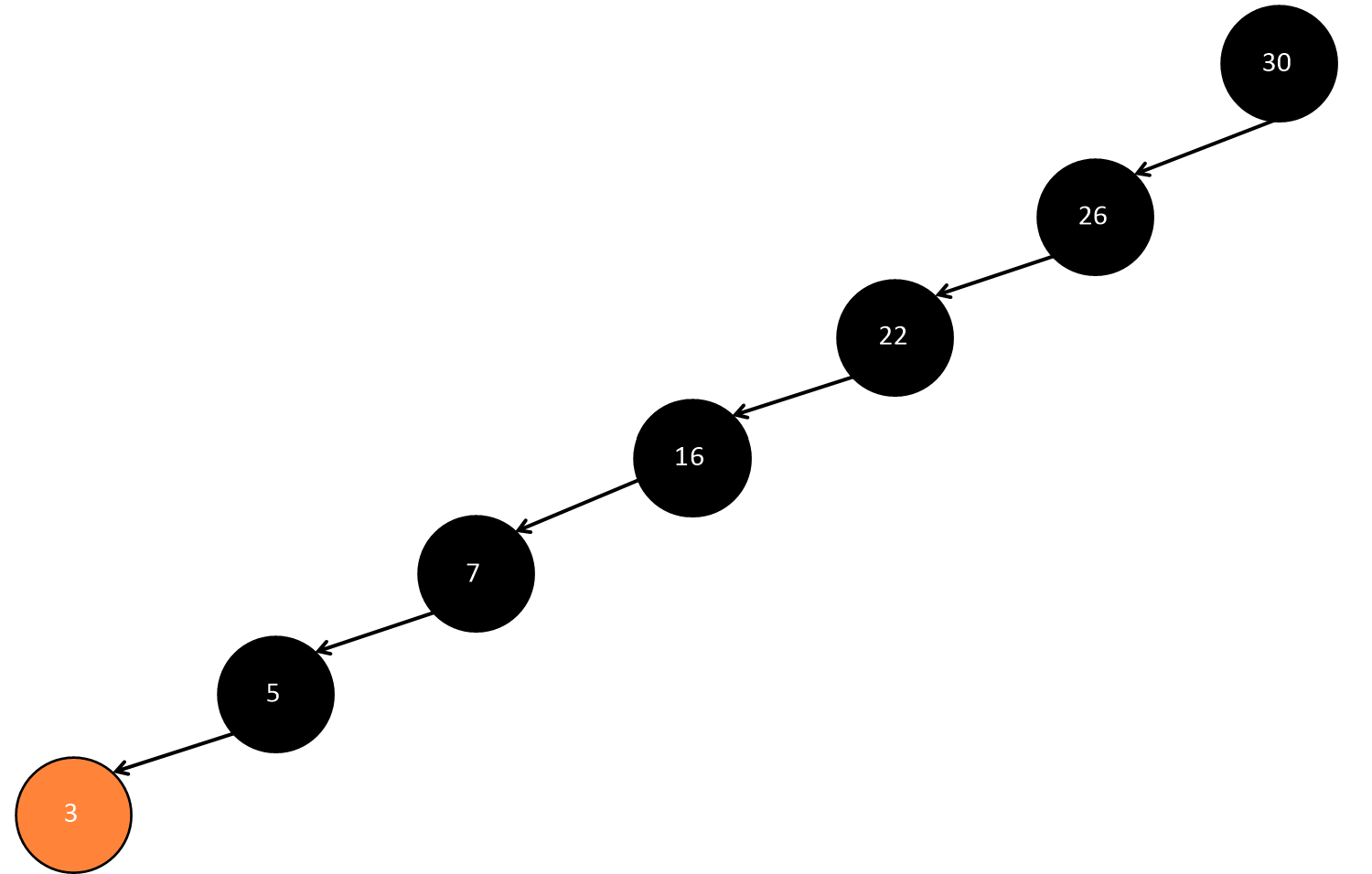
위와 같은 트리에서는 30→26→22→16→7→5→3 순으로 7번의 연산을 수행해 '3'을 찾게 될 것이다.
즉, 위와 같이 직선적으로 쭉 이어진 형태의 트리에서, n개의 노드를 가질 때 검색 연산은 O(n)의 수행 시간을 가진다.
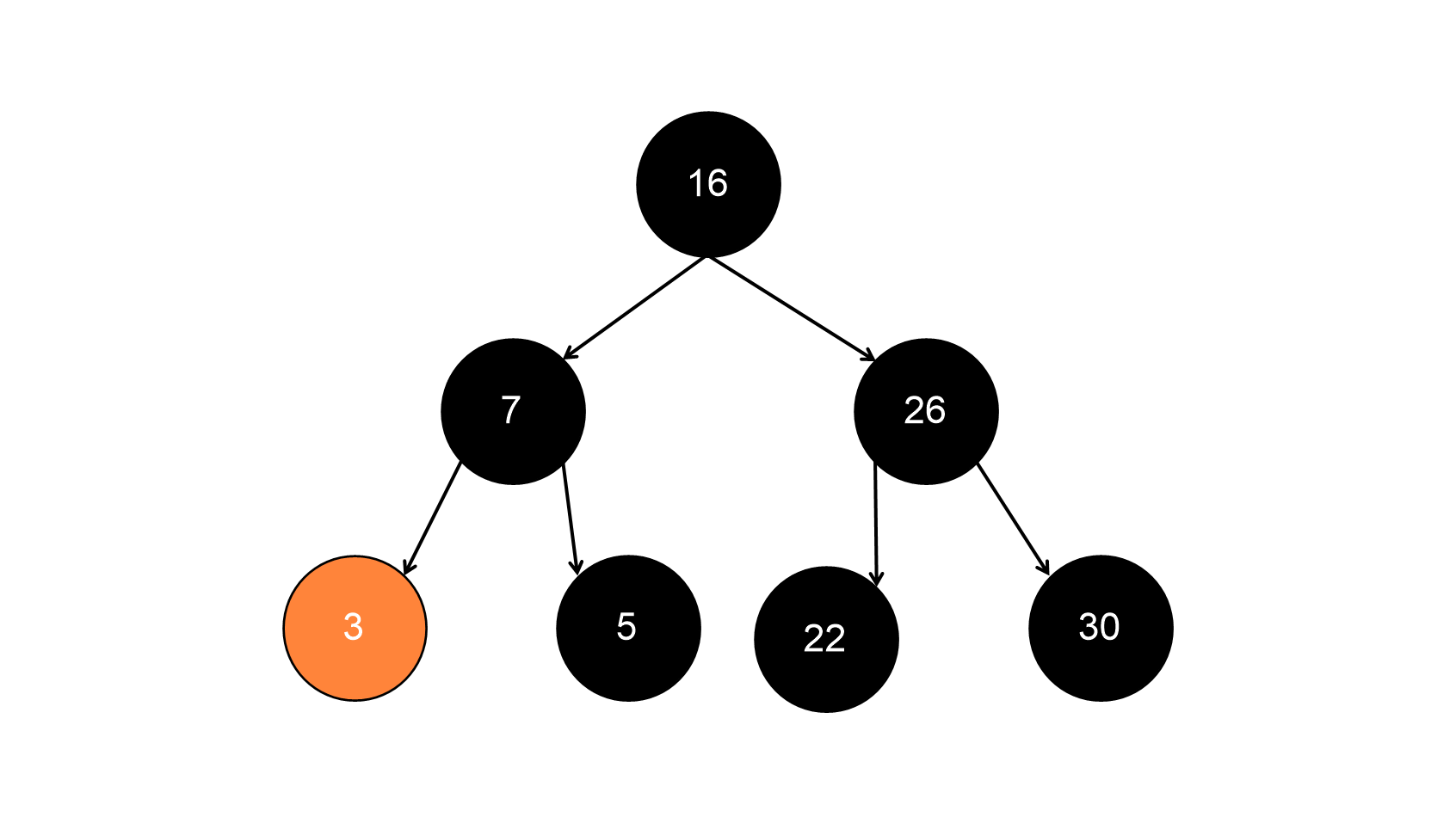
위와 같이 노드들이 각 키 값의 크기를 기준으로 고루 나누어져 있다면 어떨까?
위와 같은 트리에서 '3'을 찾는 검색 연산은 16→7→3 순으로 이진 탐색의 형태로 3번의 연산을 거쳐 끝날 것이다.
즉, 위와 같이 각 노드들이 키 값의 크기를 기준으로 고루 나누어져 있는 형태의 트리에서, n개의 노드를 가질 때 검색 연산은 O(logn)의 수행 시간을 가진다.

# 이렇게 노드들이 고루 나누어져 있는 형태를 가질 때,
트리의 '균형이 잘 잡혀있다.' 라고 표현한다. ⚖️

# 트리의 균형을 맞추면 연산의 시간 복잡도를 줄여 효율적인 검색, 삽입, 삭제가 가능해진다.

# 트리의 균형을 잡을 때는 보통 트리의 높이(height)가 특정 범위 안에서 유지되도록 하며 균형을 맞춘다.

# B-트리, AVL 트리, Red-Black 트리가 '균형을 맞춘 트리'에 속한다.

주제로 다루고 있는 Red-Black Tree에서는 균형을 맞추기 위해 'Black Height' 라는 개념을 활용한다.
결국, 이 '균형을 맞춘다'는 원론적인 개념을 이용해 접근하면 RB-tree의 삽입과 삭제 연산을 더 단순하게 설명할 수 있다.

03. RB-Tree의 노드 삽입 (insert)

개요

삽입 전 = RB-Tree의 속성 만족한 상태.

삽입 방식은 일반적인 BST와 동일.
(단, 삽입하는 노드의 색은 항상 Red이다.)

삽입 후 RB-Tree의 조건 위반 여부 확인.

2에서 RB-Tree 조건 위반 시 재조정.

삽입 후 = RB-Tree의 속성 만족한 상태.

03-1. RB-Tree의 삽입 연산 이해하기.

RB-Tree의 조건 #4.

Red의 자녀들은 항상 Black 색상을 속성으로 가진다.
( = Red는 연속적으로 존재할 수 없다!)

RB-Tree의 조건 #5.

노드 x에서 임의의 자손 nil 노드까지 내려가는 경로에서 자기 자신을 제외한 Black의 수 (Black height)는 같다.

아래 그림처럼 root 노드 아래 Black height가 n인 서브 트리 A, B가 있다고 해보자.
현재 상태에서는 A의 Black Height와 B의 Black Height가 동일할 것 이다.
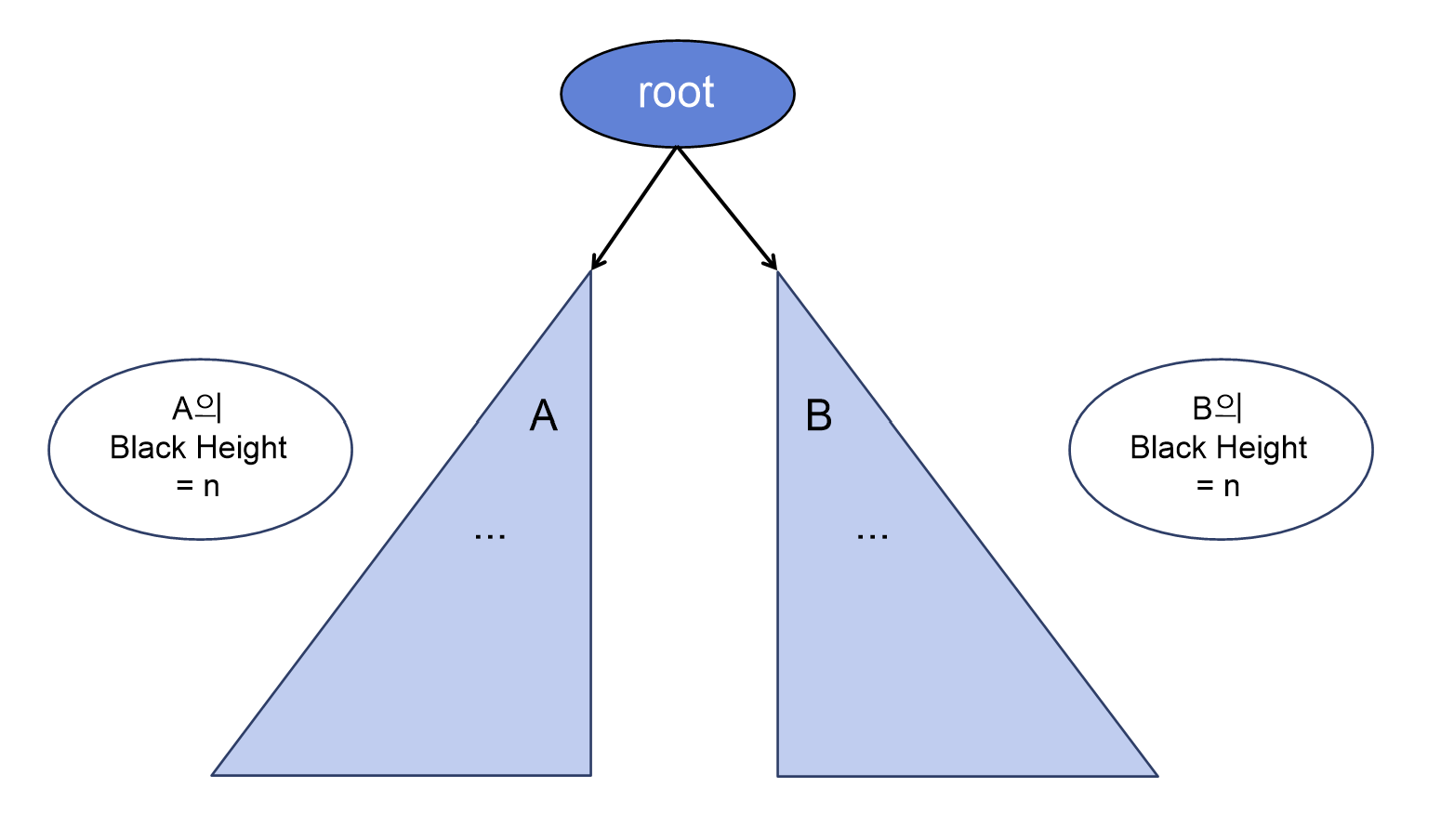
이제, 위의 서브 트리 A에 노드를 하나 삽입하는 경우를 예로 들어보자.
첫 번째로, A의 Black 노드에 Red 노드를 하나 삽입 해본다고 하자.
RB-Tree의 삽입 연산에서 새로운 노드는 항상 컬러가 Red이다.
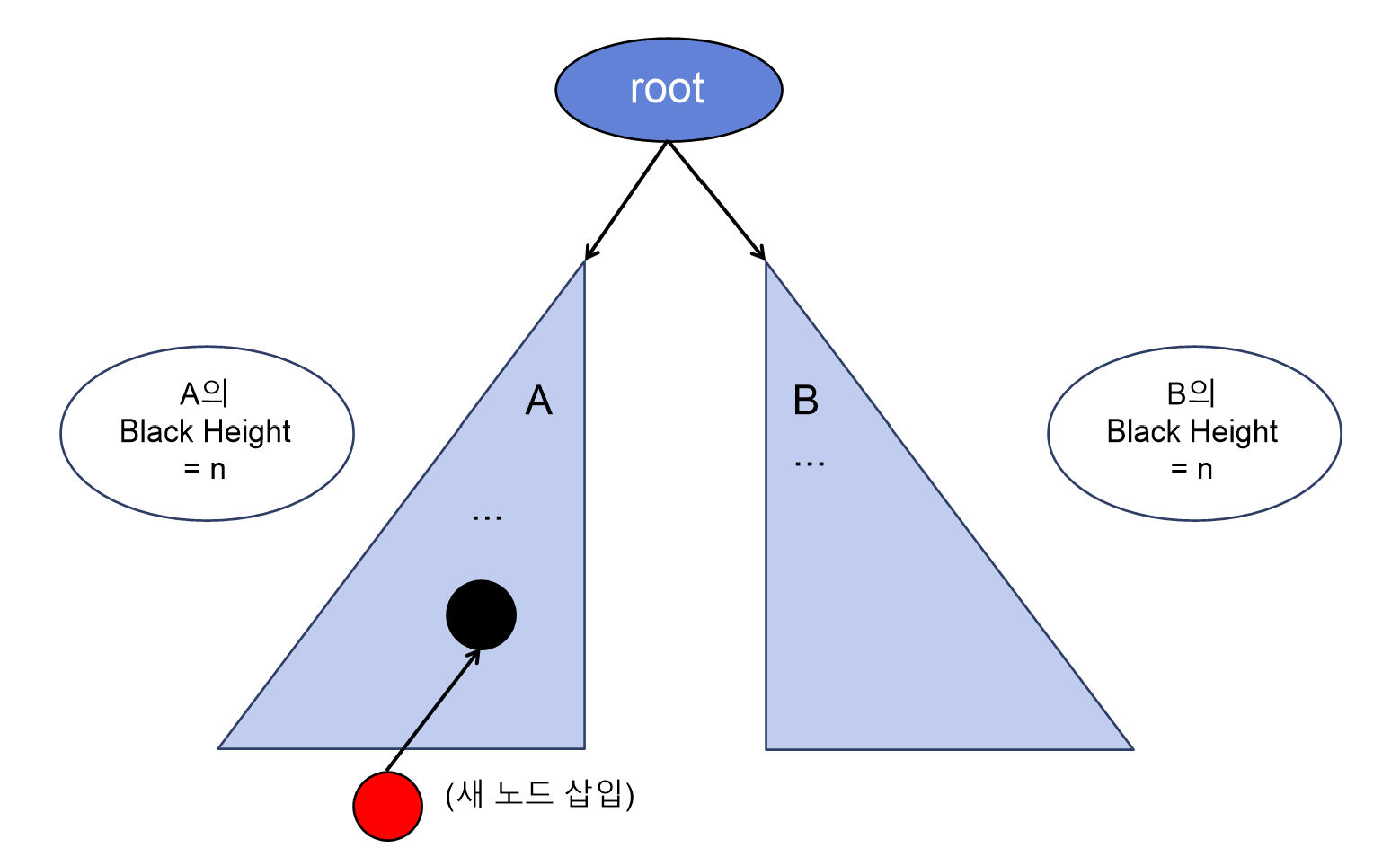
Red 노드가 연속하지도 않고, Black height에 영향을 주지도 않으므로 단순히 노드 하나만 삽입하고 삽입 연산이 끝날 것이다.
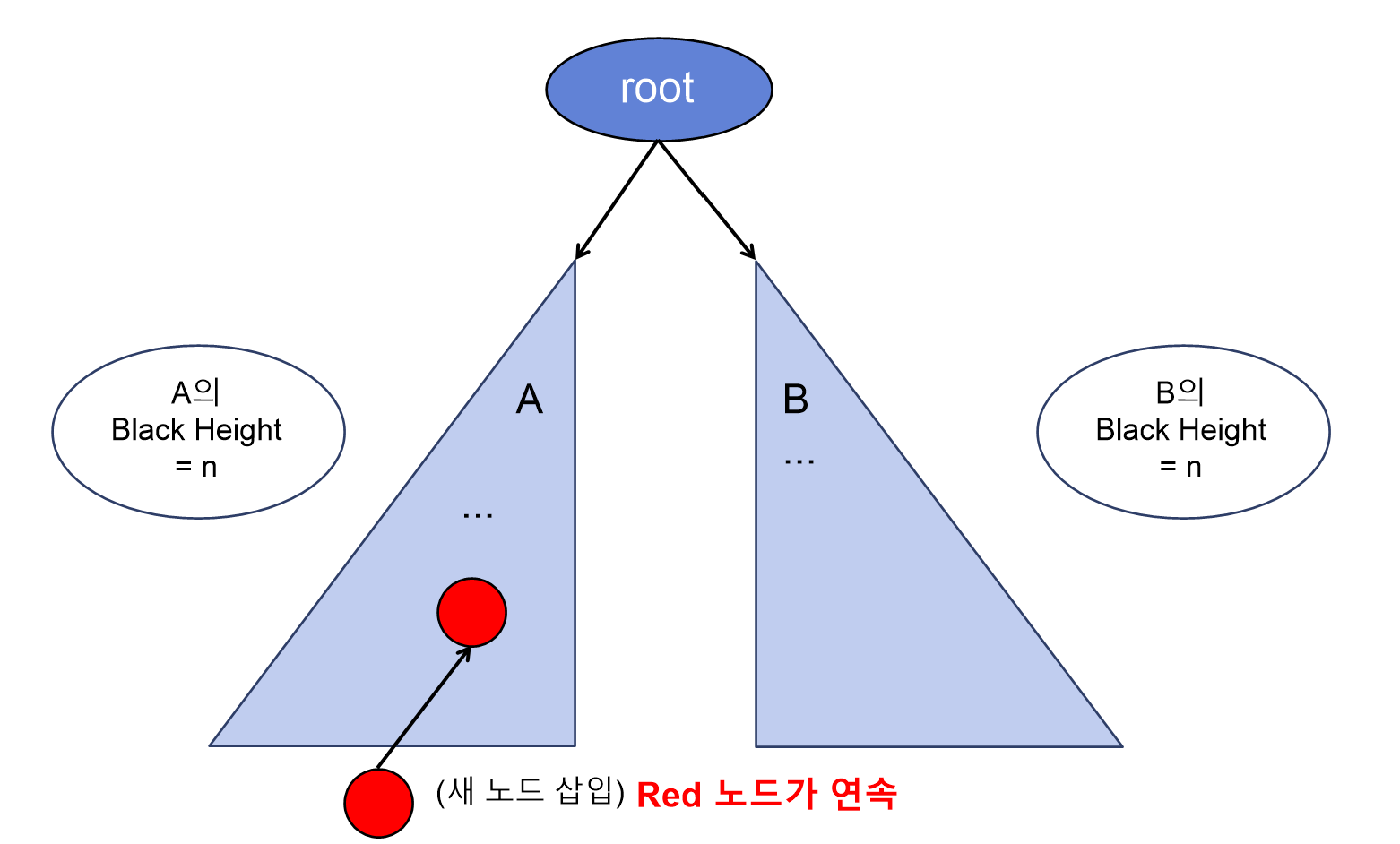
하지만, 삽입 노드의 부모도 Red였다면 어떨까?
우선, Red 노드가 연속하게 되므로 조건 #4에 어긋나게 된다.
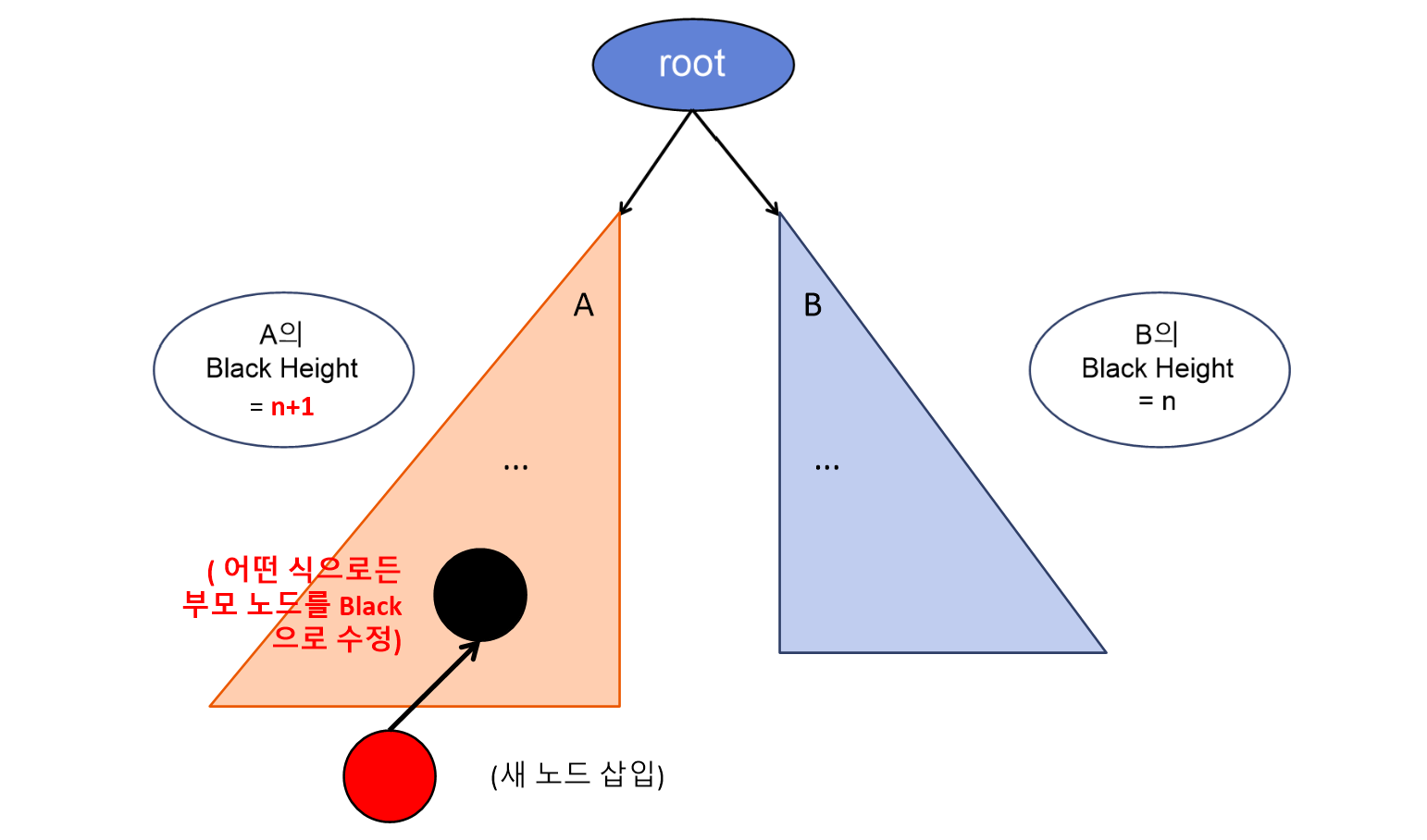
조건 #4를 해결하기 위해, 서브 트리 A에서는 새 노드의 부모를 어떤 식으로든 Black으로 고치려고 할 것이다.
하지만 이렇게 되면, A의 Black height가 n+1이 되면서 이번에는 조건#5를 위배하게 된다.
따라서, 위와 같은 경우 조건 위배를 해결하기 위해 조치를 취해야 할 것이며, 이에 따라 서브 트리 B에서 삼촌 노드를 확인하게 된다.
그리고 삼촌 노드의 형태에 따라 케이스가 크게 세 가지로 분류된다. 다시 새 노드를 삽입하던 순간으로 돌아가보자.

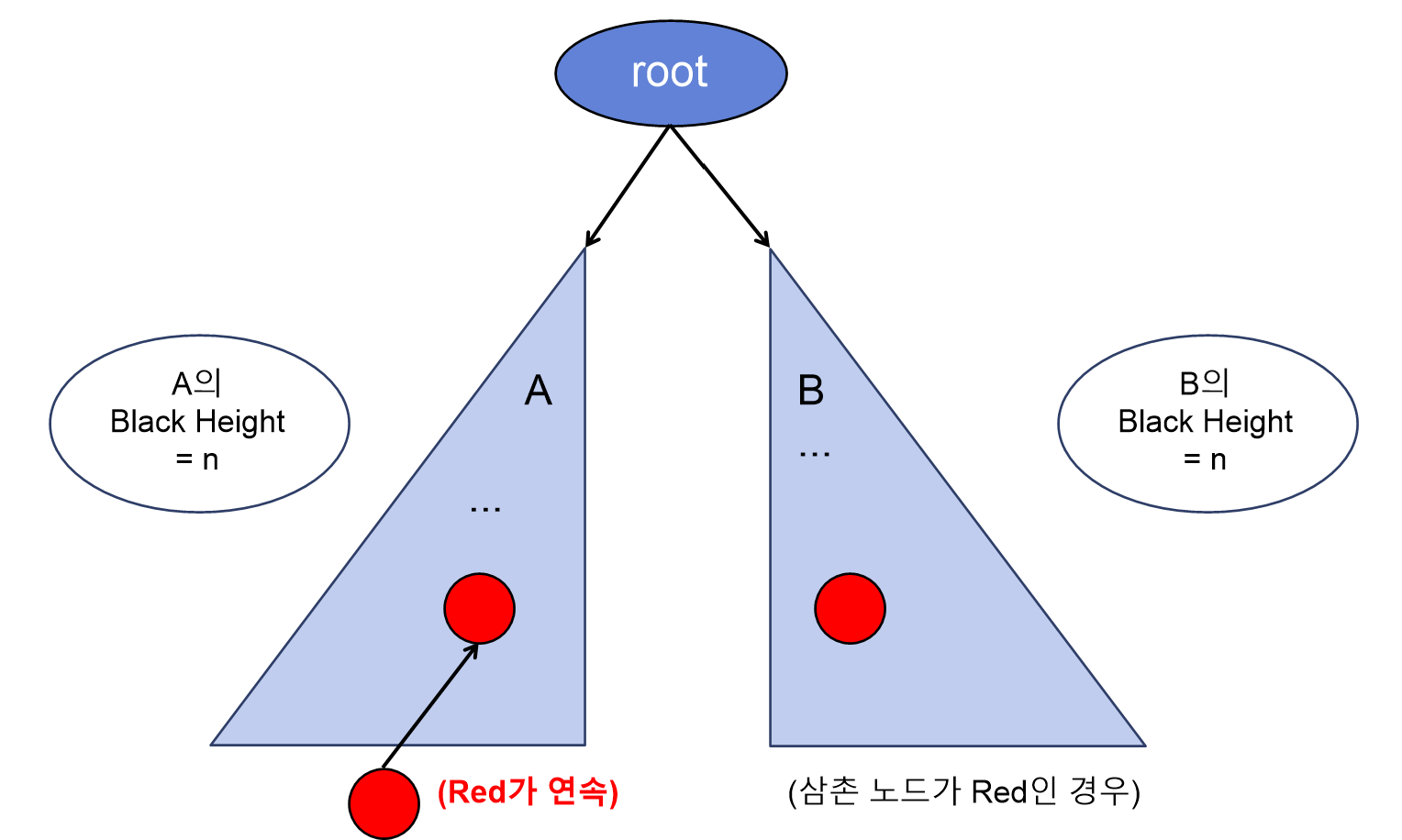
Case#1. 삼촌 노드가 Red인 경우.

→ z의 부모, 삼촌 노드를 BLACK으로, z의 조부모 노드를 RED로 수정한 뒤 조부모부터 반복적으로 조건 확인

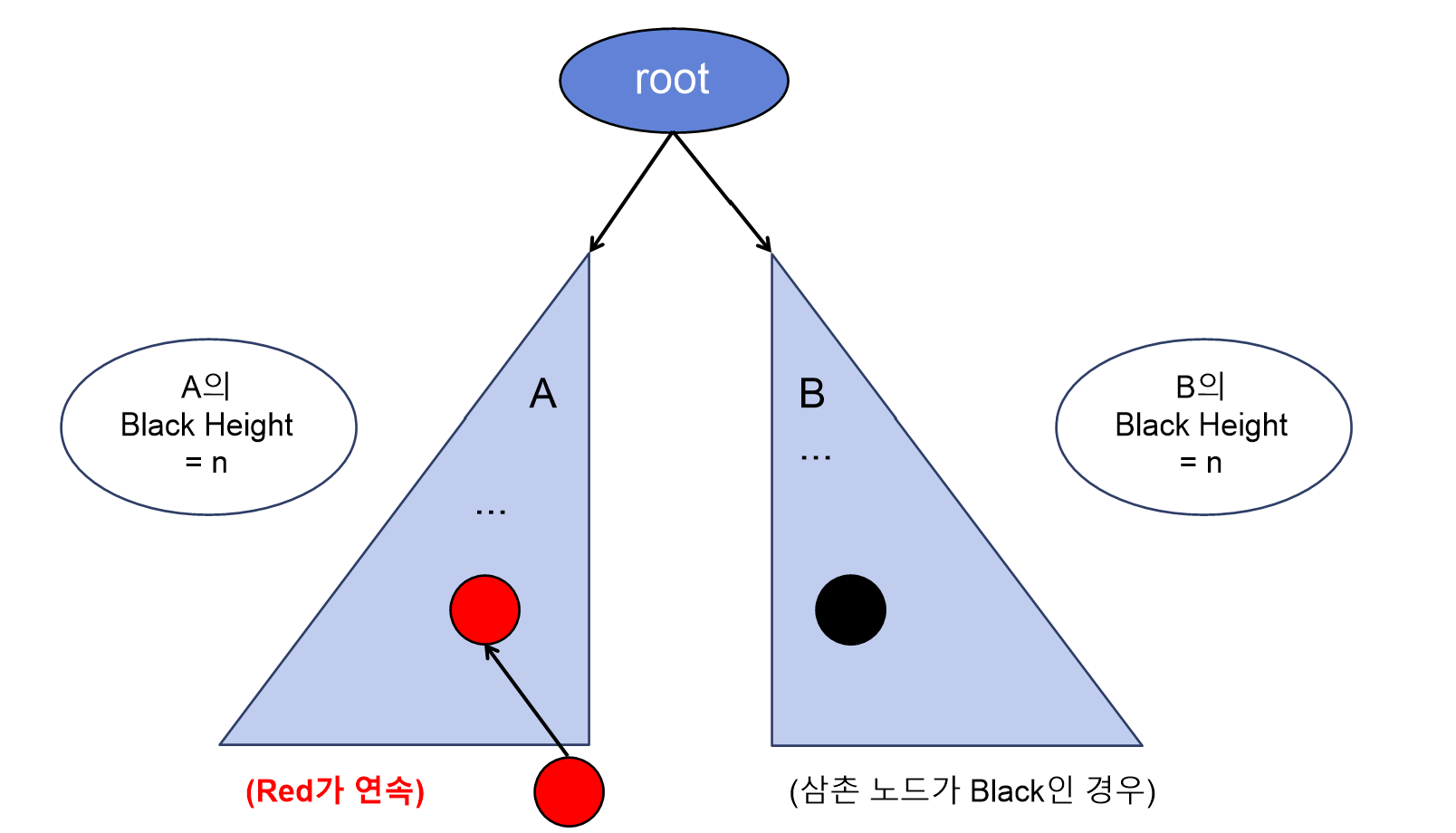
Case#2. 삼촌 노드가 Black이고, 삽입하는 노드가 오른쪽 자식인 경우.

→ z의 부모 노드를 기준으로 왼쪽 회전 후 Case#3로 수정한 뒤 이어서 해결

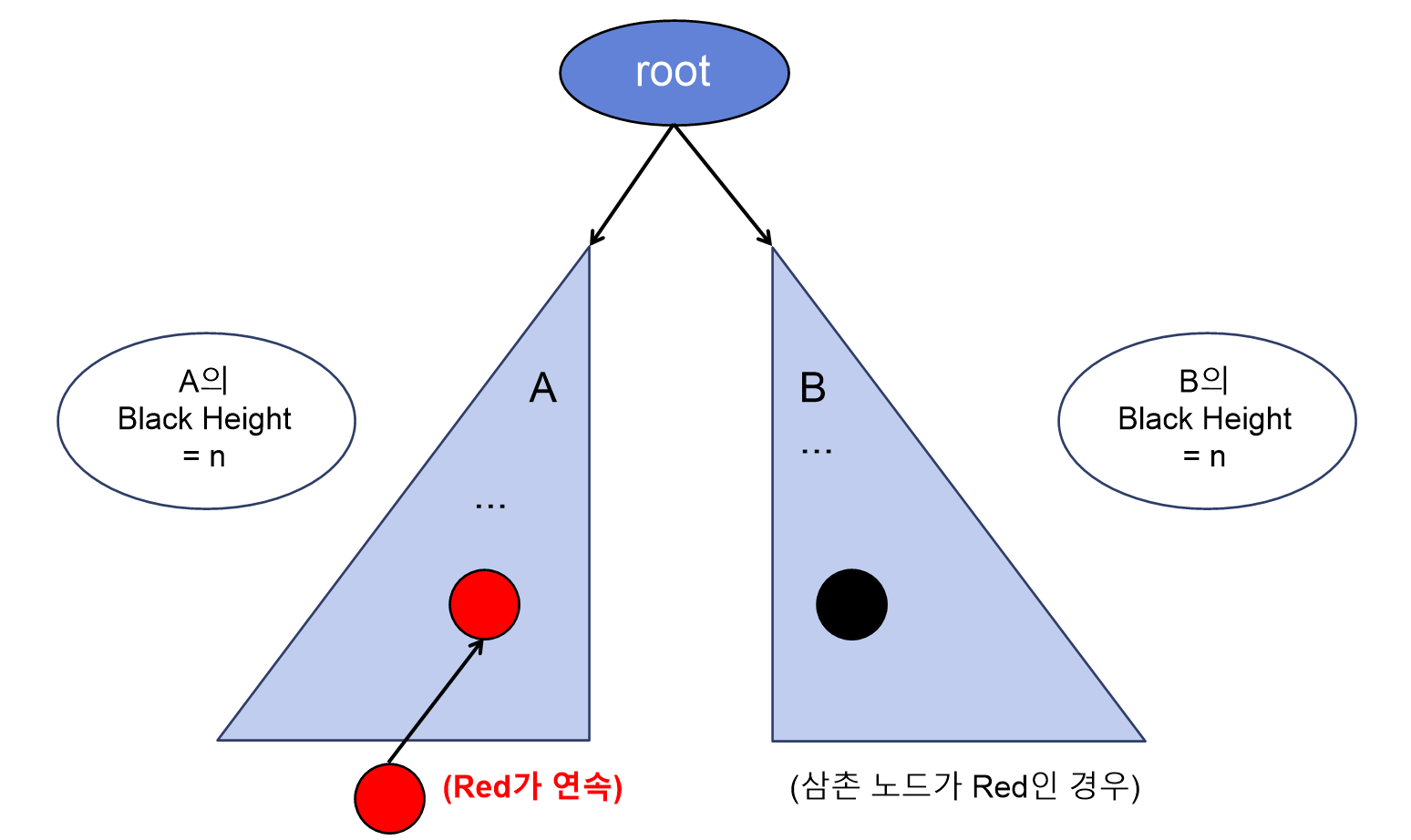
Case#3. 삼촌 노드가 Black이고, 삽입하는 노드가 왼쪽 자식인 경우.

→ z의 부모 노드를 Black으로, 조부모 노드는 RED로 수정한 뒤 조부모 노드를 기준으로 오른쪽 회전

위의 케이스들은 왼쪽, 오른쪽을 바꿔도 성립한다.

03-2. 코드 작성 (C)

void rb_insert_fixup(rbtree *t, node_t* z){
  while ( z->parent->color == RBTREE_RED)
  {
    // is parent of z left child? 
    if (z->parent == z->parent->parent->left){
      // y is uncle of z
      node_t* y = z->parent->parent->right;
      // case 1
      // when parent of z and uncle both are colored RED
      if (y->color == RBTREE_RED){
        z->parent->color = RBTREE_BLACK;
        y->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        z = z->parent->parent;
      }
      else{
        // case 2
        if (z == z->parent->right){
          z = z->parent;
          left_rotate(t,z);
        }
        // case 3
        z->parent->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        right_rotate(t,z->parent->parent);
      }
    }

    // reverse left-right
    // (when parent of z is right child)
    else {
      node_t* y = z->parent->parent->left;
      if (y->color == RBTREE_RED){
        z->parent->color = RBTREE_BLACK;
        y->color = RBTREE_BLACK;
        z->parent->parent->color= RBTREE_RED;
        z = z->parent->parent;
      }

      else{
        if (z==z->parent->left){
          z = z->parent;
          right_rotate(t,z);
        }
        z->parent->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        left_rotate(t,z->parent->parent);
      }
    }
  }
  t->root->color = RBTREE_BLACK;
}

node_t *rbtree_insert(rbtree *t, const key_t key) {
  // create 'new node z' and fill it red
  node_t* z = (node_t*)calloc(1, sizeof(node_t));
  z->color = RBTREE_RED;
  z->key = key;
  z->left = t->nil;
  z->right = t->nil;
  z->parent = t->nil;

  // x node is for comparing, and y node will be parent node of z
  node_t* x = t->root;
  node_t* y = t->nil;

  // move node x to right place
  while (x != t->nil)
  {
    y = x;
    if (z->key < x->key)
    {
      x = x->left;
    }
    else
    {
      x = x->right;
    }
  }

  z->parent = y;
  // if tree was vacant
  if (y == t->nil)
    t->root = z;

  else if (z->key < y->key)
    y->left = z;
  else
    y->right = z;

  rb_insert_fixup(t,z);
  
  return z;
}

04. RB-Tree의 노드 삭제 (erase)

개요

삭제 전: RB-Tree의 속성을 만족한 상태.

삭제 방식은 BST와 동일.

삭제 후 RB-Tree 속성 위반 여부 확인.

#2에서 RB-Tree 속성 위반 시 재조정.

삭제 후 RB-Tree의 속성을 만족한 상태.

04-1. RB-Tree의 삭제 연산 이해하기

RB-Tree의 속성 #5.

노드 x에서 임의의 자손 nil 노드까지 내려가는 경로에서의 자기 자신을 제외한 Black의 수 (Black height)는 같다.

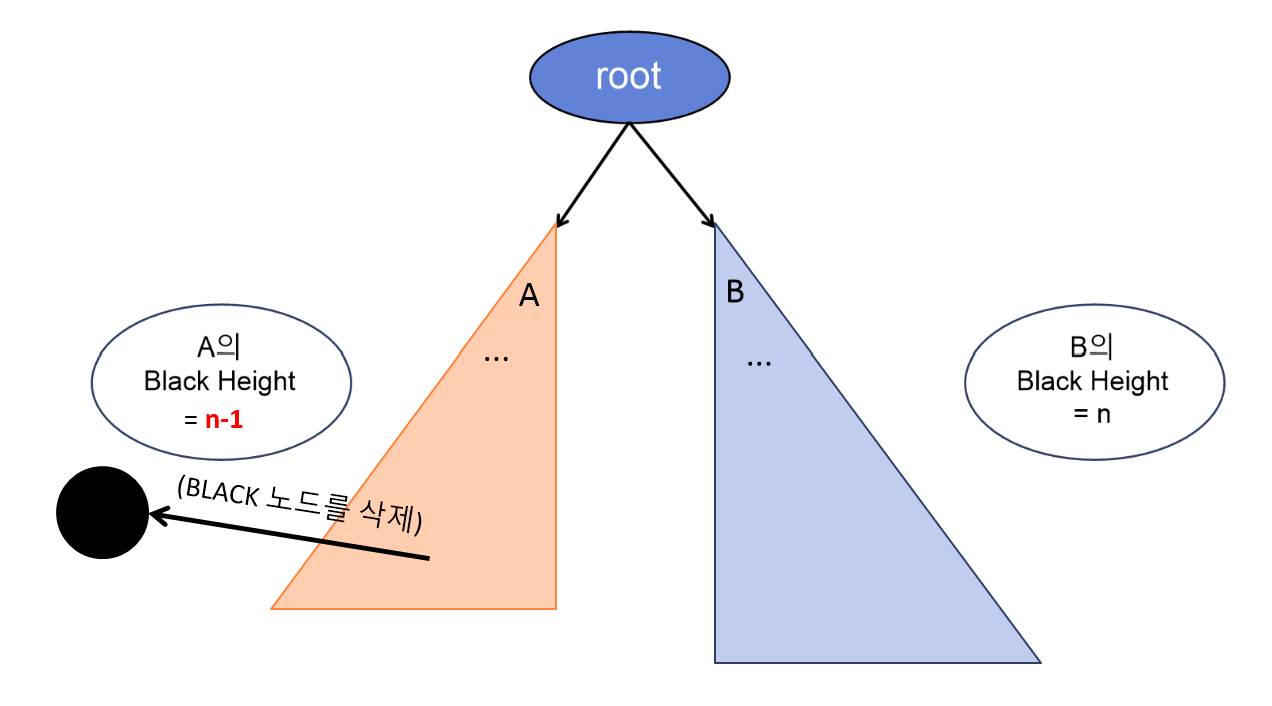
아래 그림처럼 root 노드 아래 Black height가 n인 서브 트리 A, B가 있다고 해보자.
현재 상태에서는 A의 Black Height와 B의 Black Height가 동일할 것 이다.
이제, 위의 서브 트리 A에서 노드를 하나 삭제하는 경우를 예로 들어보자.
첫 번째로, A에서 Red 노드를 하나 삭제해본다고 하자.
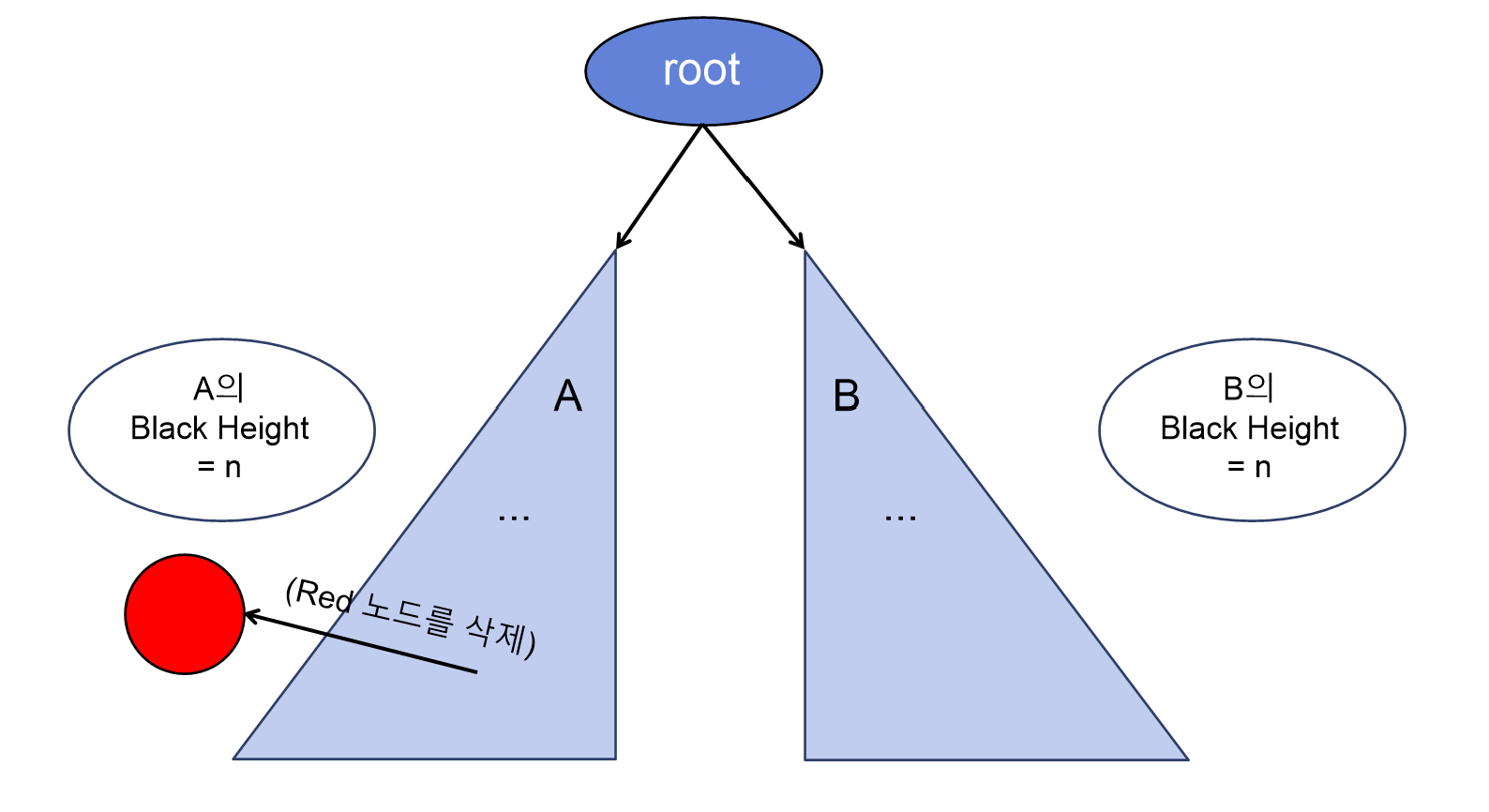
A에서 Red 노드를 삭제하더라도, A의 Black Height에 영향을 주지 않기 때문에, 여전히 A와 B의 Black Height는 n으로 동일하다.
하지만, A에서 Black 노드를 삭제한다면 어떨까?
A의 Black Height는 n-1이 되는데, B의 Black Height는 여전히 n이므로
불균형이 발생한다.
RB-Tree는 이제 이 불균형을 바로잡고 싶어한다.
그리고, 이 불균형을 맞추기 위해 A의 형제 노드 w를 서브 트리 B에서 확인한다.
그리고 이 형제 노드 w에 대해 네 가지 케이스가 있다.

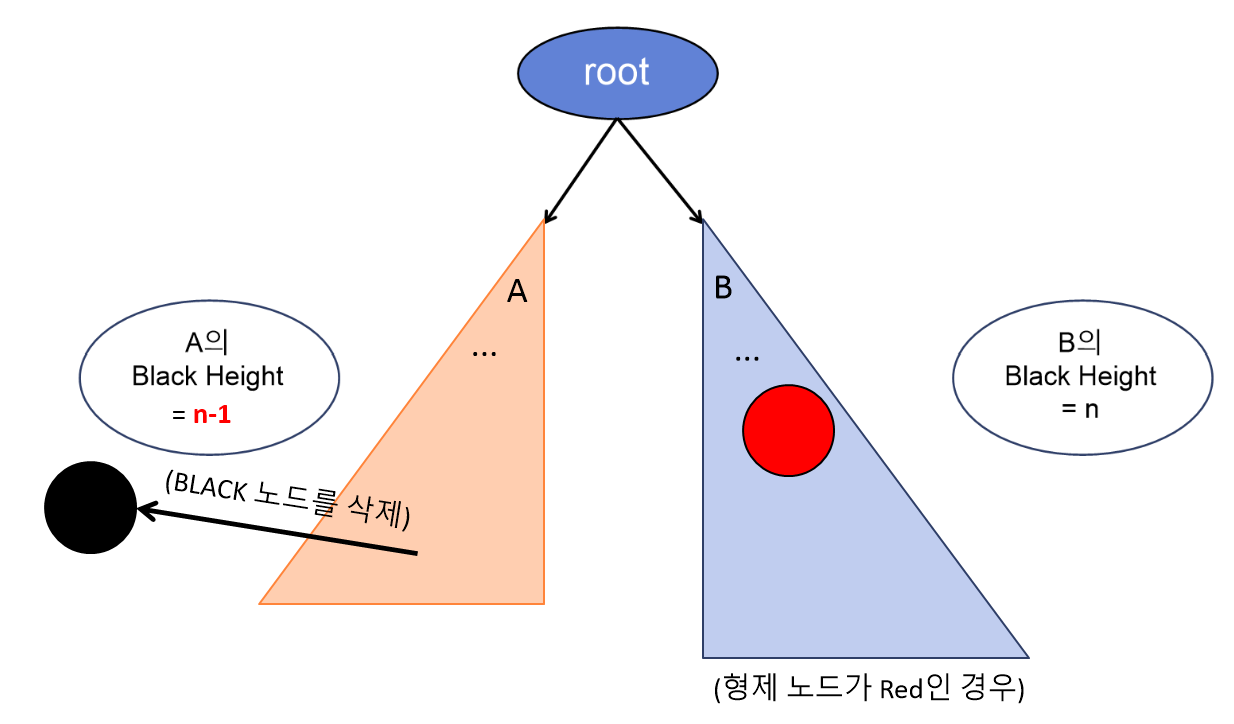
Case#1. 형제 노드 w가 Red인 경우

→ 부모 노드를 Red로, 형제 노드 w를 Black으로 만들고 왼쪽으로 회전

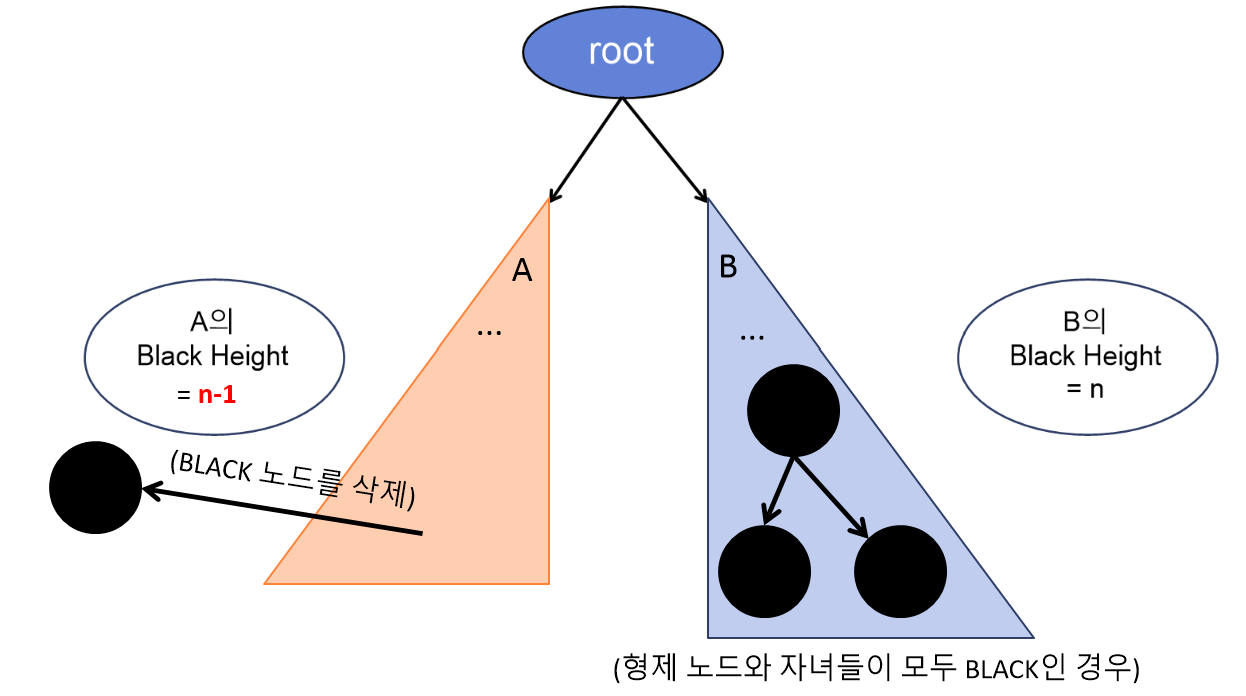
Case#2. 형제 노드 w와 그 자녀들이 모두 Black인 경우

→ 부모 노드를 Red로 만들고, x = x.p

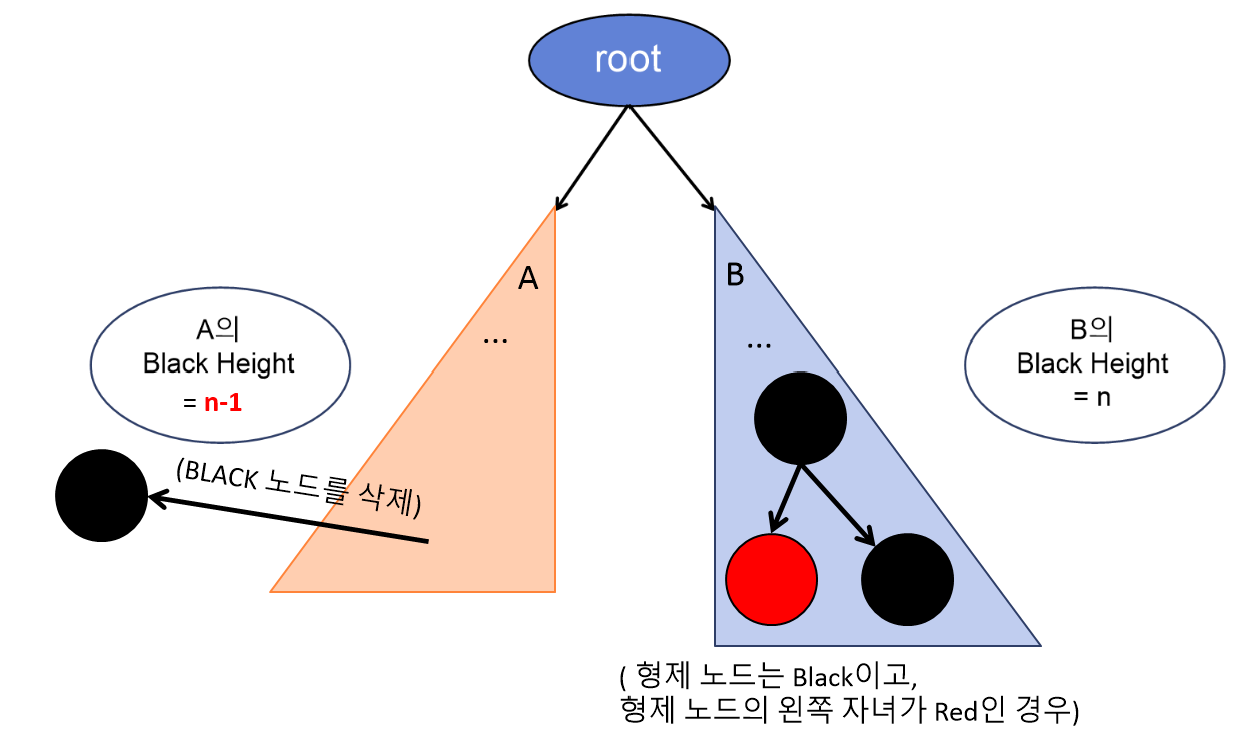
Case#3. 형제 노드 w의 왼쪽 자녀가 Red인 경우

→ 왼쪽 자식을 Black으로 수정하고, 형제 노드 w는 Red로 수정. 형제 노드 w를 기준으로 오른쪽 회전 후 x의 형제 노드로 w를 재설정.

갈색으로 표시한 노드는 'Red일 수도 있고, Black일 수도 있는' 노드를 나타낸 것이다.

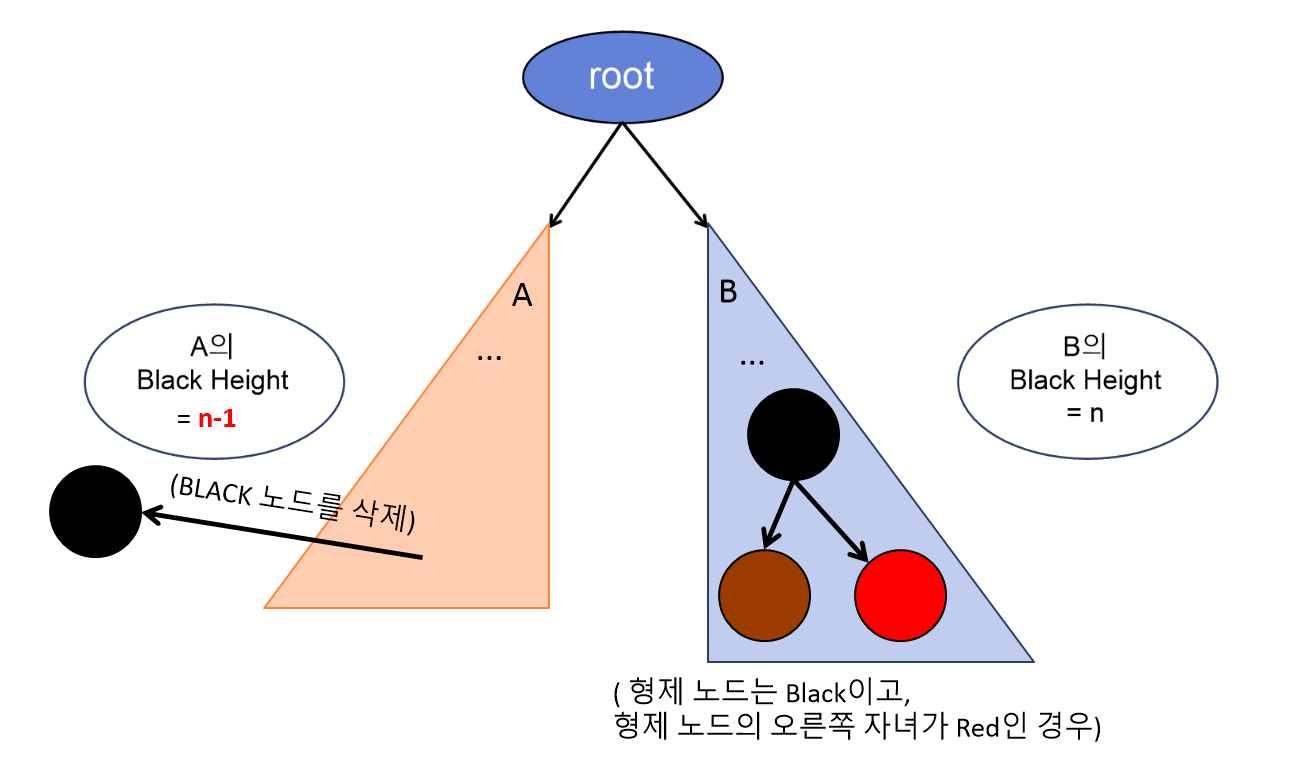
Case#4. 형제 노드는 Black, 형제 노드의 오른쪽 자녀가 Red인 경우

→ 형제 노드는 부모 노드 색으로, 부모 노드는 Black으로, 오른쪽 자식은 Black으로 수정 후 왼쪽으로 회전.

위의 케이스들은 왼쪽, 오른쪽을 바꿔도 성립한다.

04-2. 코드 작성 (C)

노드에서 출발해서 하위의 최소 노드를 찾는 함수

node_t *min_from_node(rbtree* t, node_t* n){
  if (n == t->nil)
    return NULL;
  
  node_t* tmp = n;
  // just go left till meet nill node
  while (tmp->left != t->nil)
  {
    tmp = tmp->left;
  }

  return tmp;
  
}

RB-Tree의 노드 삭제 함수

// transplant v node to place of u node
void rb_transplant(rbtree *t, node_t* u, node_t* v){
  if (u->parent == t->nil)
    t->root = v;
  else if (u == u->parent->left)
    u->parent->left = v;
  else
    u->parent->right = v;
  v->parent = u->parent;
}

void rb_erase_fixup(rbtree* t, node_t* x){
  while (x != t->root && (x == t->nil || x->color == RBTREE_BLACK))
  {
    if (x == x->parent->left){
      node_t* w = x->parent->right;
      // case 1
      if (w->color == RBTREE_RED){
        w->color = RBTREE_BLACK;
        x->parent->color = RBTREE_RED;
        left_rotate(t,x->parent);
        w = x->parent->right;
      }
      // case 2
      if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK){
        w->color = RBTREE_RED;
        x = x->parent;
      }
      // case 3
      else{
        if (w->right->color == RBTREE_BLACK){
          w->left->color = RBTREE_BLACK;
          w->color = RBTREE_RED;
          right_rotate(t,w);
          w = x->parent->right;
        }
        // case 4
        w->color = x->parent->color;
        x->parent->color = RBTREE_BLACK;
        w->right->color = RBTREE_BLACK;
        left_rotate(t,x->parent);
        x = t->root;
      }
    }

    // reverse left <-> right
    else{
      node_t* w = x->parent->left;
      if (w->color == RBTREE_RED){
        w->color = RBTREE_BLACK;
        x->parent->color = RBTREE_RED;
        right_rotate(t,x->parent);
        w = x->parent->left;
      }
      if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK){
        w->color = RBTREE_RED;
        x = x->parent;
      }
      else{
        if (w->left->color == RBTREE_BLACK){
          w->right->color = RBTREE_BLACK;
          w->color = RBTREE_RED;
          left_rotate(t,w);
          w = x->parent->left;
        }
        w->color = x->parent->color;
        x->parent->color = RBTREE_BLACK;
        w->left->color = RBTREE_BLACK;
        right_rotate(t,x->parent);
        x = t->root;
      }
    }
  }
  x->color = RBTREE_BLACK;
}

int rbtree_erase(rbtree *t, node_t *p) {
  node_t *y = p;
  node_t *x = NULL;
  color_t y_original_color = y->color;

  if (p->left == t->nil){
    x = p->right;
    rb_transplant(t,p,p->right);
  }
  else if (p->right == t->nil){
    x = p->left;
    rb_transplant(t,p,p->left);
  }
  else {
    y = min_from_node(t, p->right);
    y_original_color = y->color;
    x = y->right;
    if (y != p->right){
      rb_transplant(t,y,y->right);
      y->right = p->right;
      y->right->parent = y;
    }
    else{
      if (y->parent != t->nil)
        x->parent = y;
    }
    rb_transplant(t,p,y);
    y->left = p->left;
    y->left->parent = y;
    y->color = p->color;
  }

  if (y_original_color == RBTREE_BLACK)
    rb_erase_fixup(t,x);
  
  // reclaim node p
  free(p);

  return 0;
}

05. RB-Tree와 AVL Tree의 비교

구분	Red-Black Tree	AVL Tree
BST인가?	Yes	Yes
삽입 / 삭제 / 검색의 시간 복잡도	O(logN)	O(logN)
삽입 / 삭제 성능	AVL 트리에 비해 빠르다.	RB-Tree에 비해 느리다.
검색 성능	AVL 트리에 비해 느리다.	RB-Tree에 비해 빠르다.
균형을 잡는 방식	RB-Tree 속성들을 만족하도록	balance factor {-1,0,1}이 되도록.
응용 사례	linux kernel 내부 Java Tree Map 구현 C++ std::map 구현	dictionary 한 번 만들어놓고, 삽입 / 삭제 거의 없고 검색이 대부분인 경우

:: 참고 자료 / 이미지 출처

Red-Black Tree - Wikipedia.
https://en.wikipedia.org/wiki/Red%E2%80%93black_tree
(1부) 레드블랙트리(red-black tree)의 기본 개념과 특징을 살펴보고, 삽입 때 레드블랙트리가 어떻게 동작하는지를 아주 자세히 설명합니다~ 헷갈리시는 분들 커몬요
https://youtu.be/2MdsebfJOyM?si=Iug0cPDKRtrGfGyo
(2부) 레드블랙트리(red-black tree)의 삭제는 어떻게 동작할까요? 시간 복잡도는 어떻게 될까요? AVL 트리와 차이는 무엇일까요? 이 영상으로 후련하게 해결하세요 :)
https://www.youtube.com/watch?v=6drLl777k-E

@developer/takealittle.time

능동적으로 사고하고, 성장하기 위한. 🌱

이전 포스트

git의 bare repository, mirror 명령어, git CLI의 간단한 사용

다음 포스트

[WIL] Jungle 5주차 Red-Black Tree 레드 블랙 트리 요점 정리와 코드 작성(C)

Jungle

✅ 이번 주차 학습을 진행하며 어려웠던 점

→ 이에 대해 얻은 인사이트를 공유하고자 한다.

< Red-Black Tree >

01. RB-tree의 속성

RB-tree의 속성.

02. RB-Tree가 균형을 잡는 방법?

들어가기 전에.

코드 작성 :: 필요한 구조체 등 선언

코드 작성 :: 트리 초기화 함수, 삭제 함수

회전 C 코드

<RB-Tree의 삽입과 삭제에 앞서>

* '균형을 맞춘다'는 아이디어 🔍

# 이렇게 노드들이 고루 나누어져 있는 형태를 가질 때,
트리의 '균형이 잘 잡혀있다.' 라고 표현한다. ⚖️

03. RB-Tree의 노드 삽입 (insert)

개요

03-1. RB-Tree의 삽입 연산 이해하기.

RB-Tree의 조건 #4.

RB-Tree의 조건 #5.

Case#1. 삼촌 노드가 Red인 경우.

Case#2. 삼촌 노드가 Black이고, 삽입하는 노드가 오른쪽 자식인 경우.

Case#3. 삼촌 노드가 Black이고, 삽입하는 노드가 왼쪽 자식인 경우.

03-2. 코드 작성 (C)

04. RB-Tree의 노드 삭제 (erase)

개요

04-1. RB-Tree의 삭제 연산 이해하기

RB-Tree의 속성 #5.

Case#1. 형제 노드 w가 Red인 경우

Case#2. 형제 노드 w와 그 자녀들이 모두 Black인 경우

Case#3. 형제 노드 w의 왼쪽 자녀가 Red인 경우

Case#4. 형제 노드는 Black, 형제 노드의 오른쪽 자녀가 Red인 경우

04-2. 코드 작성 (C)

05. RB-Tree와 AVL Tree의 비교

:: 참고 자료 / 이미지 출처

git의 bare repository, mirror 명령어, git CLI의 간단한 사용

[WIL] Jungle 6주차 Malloc-Lab :: 동적 할당기의 구현 (C)

0개의 댓글

관련 채용 정보

[WIL] Jungle 5주차 Red-Black Tree 레드 블랙 트리 요점 정리와 코드 작성(C)

Jungle

✅ 이번 주차 학습을 진행하며 어려웠던 점

→ 이에 대해 얻은 인사이트를 공유하고자 한다.

< Red-Black Tree >

01. RB-tree의 속성

RB-tree의 속성.

02. RB-Tree가 균형을 잡는 방법?

들어가기 전에.

코드 작성 :: 필요한 구조체 등 선언

코드 작성 :: 트리 초기화 함수, 삭제 함수

회전 C 코드

<RB-Tree의 삽입과 삭제에 앞서>

* '균형을 맞춘다'는 아이디어 🔍

# 이렇게 노드들이 고루 나누어져 있는 형태를 가질 때, 트리의 '균형이 잘 잡혀있다.' 라고 표현한다. ⚖️

03. RB-Tree의 노드 삽입 (insert)

개요

03-1. RB-Tree의 삽입 연산 이해하기.

RB-Tree의 조건 #4.

RB-Tree의 조건 #5.

Case#1. 삼촌 노드가 Red인 경우.

Case#2. 삼촌 노드가 Black이고, 삽입하는 노드가 오른쪽 자식인 경우.

Case#3. 삼촌 노드가 Black이고, 삽입하는 노드가 왼쪽 자식인 경우.

03-2. 코드 작성 (C)

04. RB-Tree의 노드 삭제 (erase)

개요

04-1. RB-Tree의 삭제 연산 이해하기

RB-Tree의 속성 #5.

Case#1. 형제 노드 w가 Red인 경우

Case#2. 형제 노드 w와 그 자녀들이 모두 Black인 경우

Case#3. 형제 노드 w의 왼쪽 자녀가 Red인 경우

Case#4. 형제 노드는 Black, 형제 노드의 오른쪽 자녀가 Red인 경우

04-2. 코드 작성 (C)

05. RB-Tree와 AVL Tree의 비교

:: 참고 자료 / 이미지 출처

git의 bare repository, mirror 명령어, git CLI의 간단한 사용

[WIL] Jungle 6주차 Malloc-Lab :: 동적 할당기의 구현 (C)

0개의 댓글

관련 채용 정보

# 이렇게 노드들이 고루 나누어져 있는 형태를 가질 때,
트리의 '균형이 잘 잡혀있다.' 라고 표현한다. ⚖️