위상 정렬 (Topological Sorting)의 개념, Baekjoon - [Gold III] 줄 세우기 - 2252

@developer/takealittle.time·2024년 9월 20일

Sort jungle krafton

Jungle

목록 보기

5/21

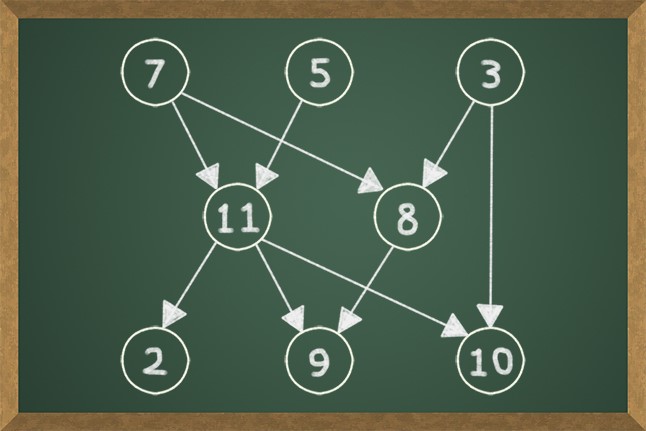
00. 위상 정렬

'순서가 정해져 있는 일련의 작업'을 차례대로 수행해야 할 때 사용하는 정렬 알고리즘.

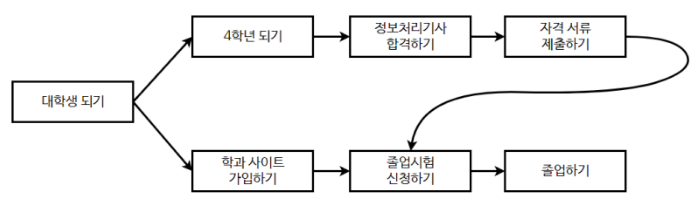
ex) 대학생 되기 → 학과 사이트 가입하기 → 4학년 되기 → 정보처리기사 합격하기 → 자격서류 제출하기 → 졸업시험 신청하기 → 졸업하기
위상 정렬은 '사이클이 없는 방향 그래프(DAG: Directed Acyclic Graph'에서 사용 가능.
- 사이클이 발생하는 경우 시작점도 찾을 수 없고, 정렬 수행 도중 모든 원소를 방문하기 전에 큐가 비어버린다.

01. '진입차수'와 '진출차수'

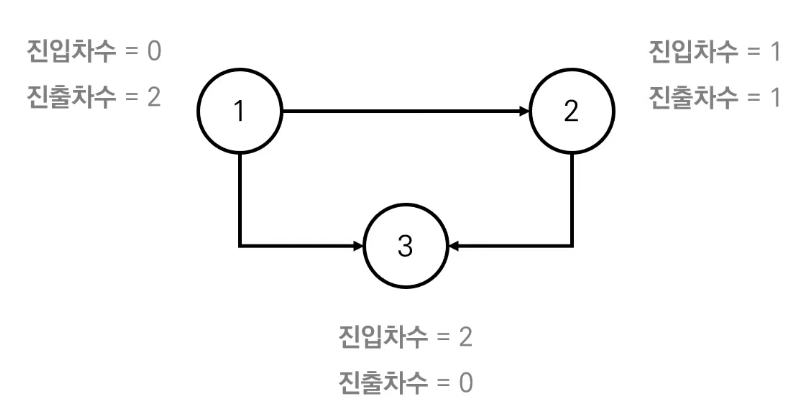
진입차수 (Indegree): 특정한 노드로 들어오는 간선의 개수
진출차수 (Outdegree): 특정한 노드에서 나가는 간선의 개수

02. 위상 정렬의 동작 과정

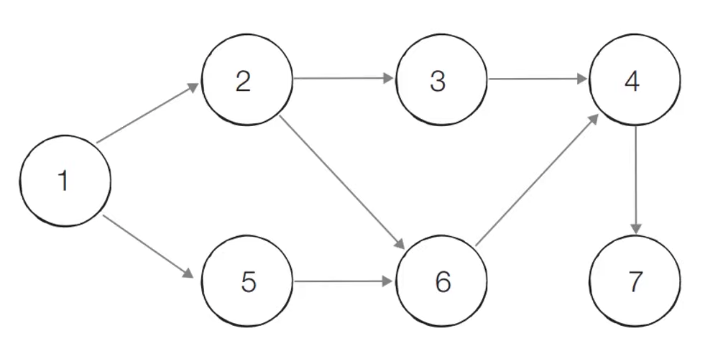
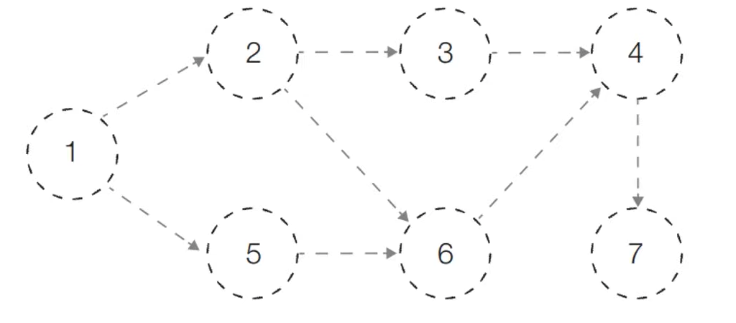
0. 위상 정렬을 수행할 그래프는 위처럼 사이클이 없는 방향 그래프(DAG)이어야 한다.

진입차수가 0인 모든 노드를 큐에 삽입.
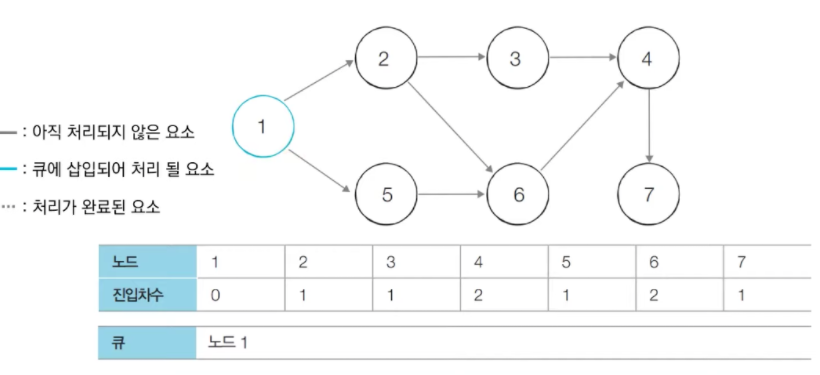
- 현재 1번 노드의 진입차수만 0이므로, 큐에 1번 노드만 삽입.
큐에 있는 1번 노드를 꺼내고, 1번 노드와 연결되어 있는 간선들을 제거.
→ 2번 노드, 5번 노드의 진입차수가 0이 됨.
→ 2번 노드, 5번 노드 큐에 삽입.
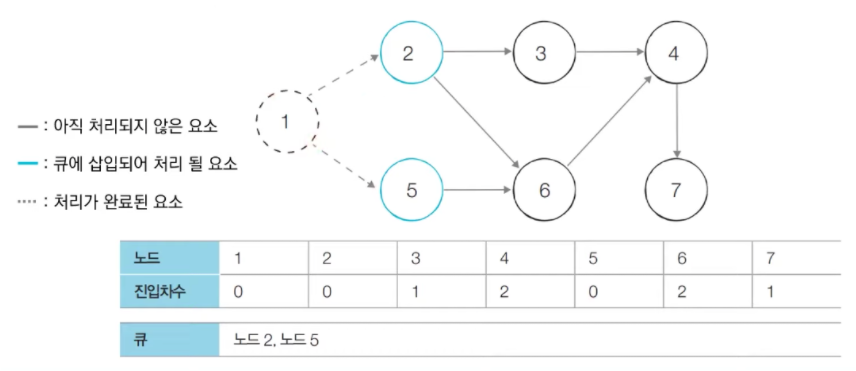
큐에 있는 2번 노드를 꺼내고, 2번 노드와 연결된 간선들을 제거.
→ 3번 노드의 진입차수가 0이 됨.
→ 3번 노드를 큐에 삽입.
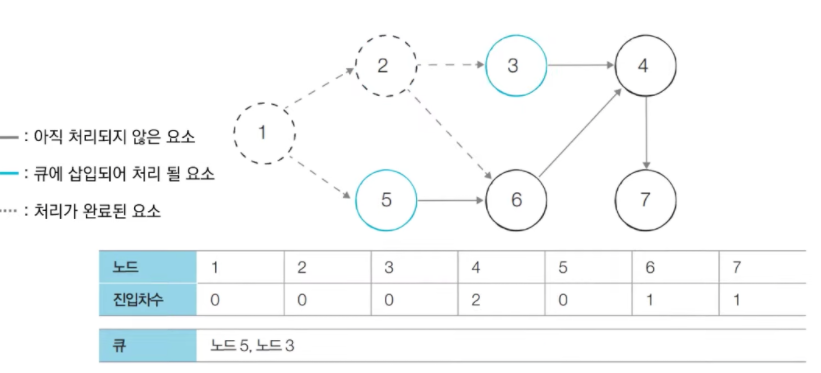
큐에 있는 5번 노드를 꺼내고, 5번 노드와 연결된 간선들을 제거.
→ 6번 노드의 진입차수가 0이 됨.
→ 6번 노드를 큐에 삽입.
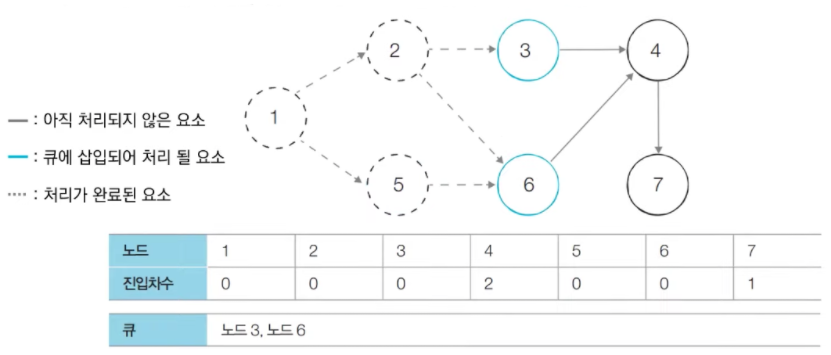
큐에 있는 3번 노드를 꺼내고, 3번 노드와 연결된 간선들을 제거.
→ 새롭게 진입차수가 0이 되는 노드들이 없음.
→ 넘어감.
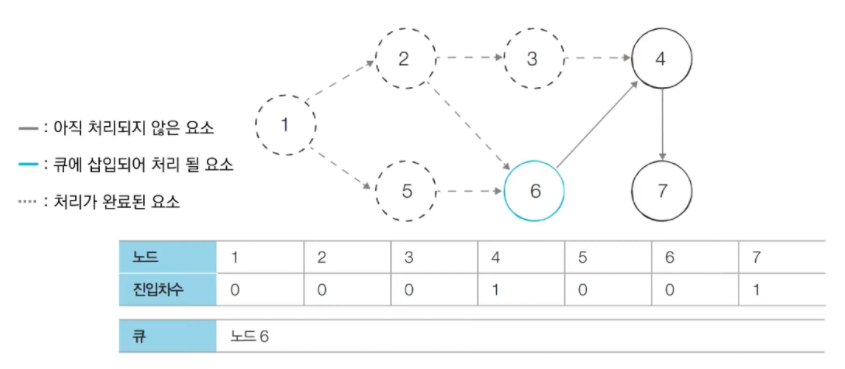
큐에 있는 6번 노드를 꺼내고, 6번 노드와 연결된 간선들을 제거.
→ 4번 노드의 진입차수가 0이 됨.
→ 4번 노드를 큐에 삽입.

~. 위와 동일한 로직으로 큐에 있는 노드들을 꺼내고, 꺼낸 노드와 연결된 간선들을 제거.
→ 새롭게 진입차수가 0이 되는 노드를 큐에 삽입.

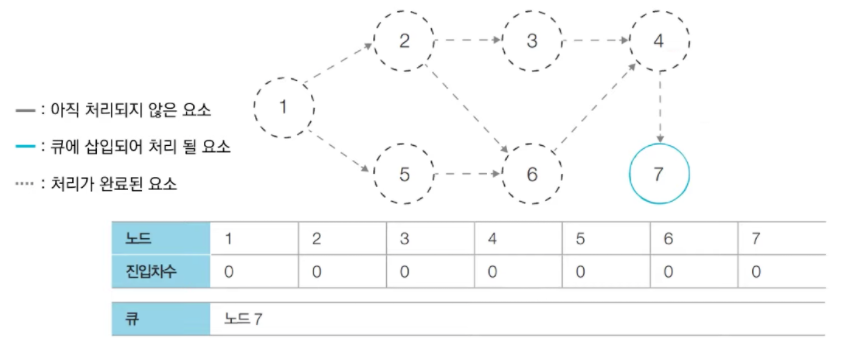
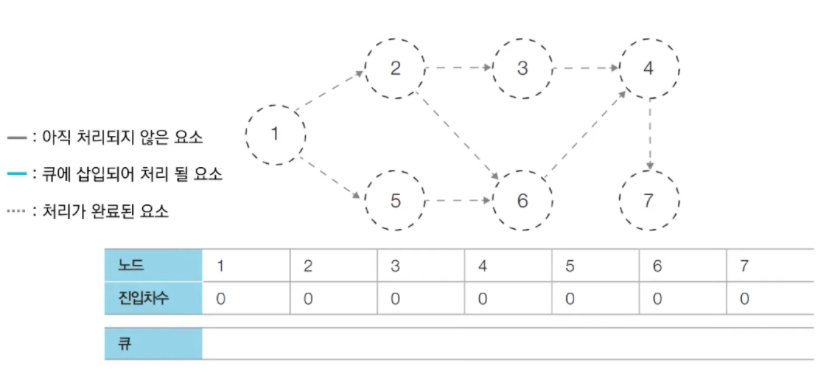
<결과> 1 → 2 → 5 → 3 → 6 → 4 → 7

위상 정렬의 답안은 여러가지가 될 수 있다.
ex) 1 → 5 → 2 → 3 → 6 → 4 → 7 도 답이 될 수 있다.
*한 단계에서 큐에 들어가는 원소가 2개 이상인 경우 발생

03. 위상 정렬의 특징

위상 정렬은 사이클이 없는 방향 그래프(DAG)에 대해서만 수행할 수 있다.
위상 정렬에서는 여러가지 답이 존재할 수 있다.
사이클이 존재하면 모든 원소를 방문하기 전에 큐가 비어버린다.
큐가 아니라, 스택을 이용한 DFS로도 위상 정렬을 구현할 수 있다.

[Gold III] 줄 세우기 - 2252

성능 요약
메모리: 38408 KB, 시간: 164 ms

분류
방향 비순환 그래프, 그래프 이론, 위상 정렬

문제 설명
N명의 학생들을 키 순서대로 줄을 세우려고 한다. 각 학생의 키를 직접 재서 정렬하면 간단하겠지만, 마땅한 방법이 없어서 두 학생의 키를 비교하는 방법을 사용하기로 하였다. 그나마도 모든 학생들을 다 비교해 본 것이 아니고, 일부 학생들의 키만을 비교해 보았다.

일부 학생들의 키를 비교한 결과가 주어졌을 때, 줄을 세우는 프로그램을 작성하시오.

입력
첫째 줄에 N(1 ≤ N ≤ 32,000), M(1 ≤ M ≤ 100,000)이 주어진다. M은 키를 비교한 회수이다. 다음 M개의 줄에는 키를 비교한 두 학생의 번호 A, B가 주어진다. 이는 학생 A가 학생 B의 앞에 서야 한다는 의미이다.

학생들의 번호는 1번부터 N번이다.

출력
첫째 줄에 학생들을 앞에서부터 줄을 세운 결과를 출력한다. 답이 여러 가지인 경우에는 아무거나 출력한다.

00. 발상

위에서 작성한 위상정렬의 개념 그대로 따라가면 된다.
학생 A, B에 대해 A는 반드시 B보다 앞에 와야하므로 A -> B의 간선이 있다고 생각한다. 이렇게 되면 B의 진입차수가 1 증가하는 것이다.

01. 코드 작성

import sys
from collections import deque
input = sys.stdin.readline

N, M = map(int, input().split())

indegree = [0] * (N+1)

graph = [[] for _ in range(N+1)]
for _ in range(M):
    A, B = map(int, input().split())
    graph[A].append(B)
    indegree[B] += 1

def topology(N):
    result = []
    q = deque()
    
    for i in range(1, N+1):
        if indegree[i] == 0:
            q.append(i)
    
    while q:
        current = q.popleft()
        result.append(current)

        for neighbor in graph[current]:
            indegree[neighbor] -= 1
            if indegree[neighbor] == 0:
                q.append(neighbor)
    
    for res in result:
        print(res,end=' ')

topology(N)