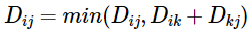
00. 최단 거리 알고리즘
-
그래프 상에서 노드 간 탐색 비용을 최소화하는 알고리즘.
-
대표적인 최단 거리 알고리즘
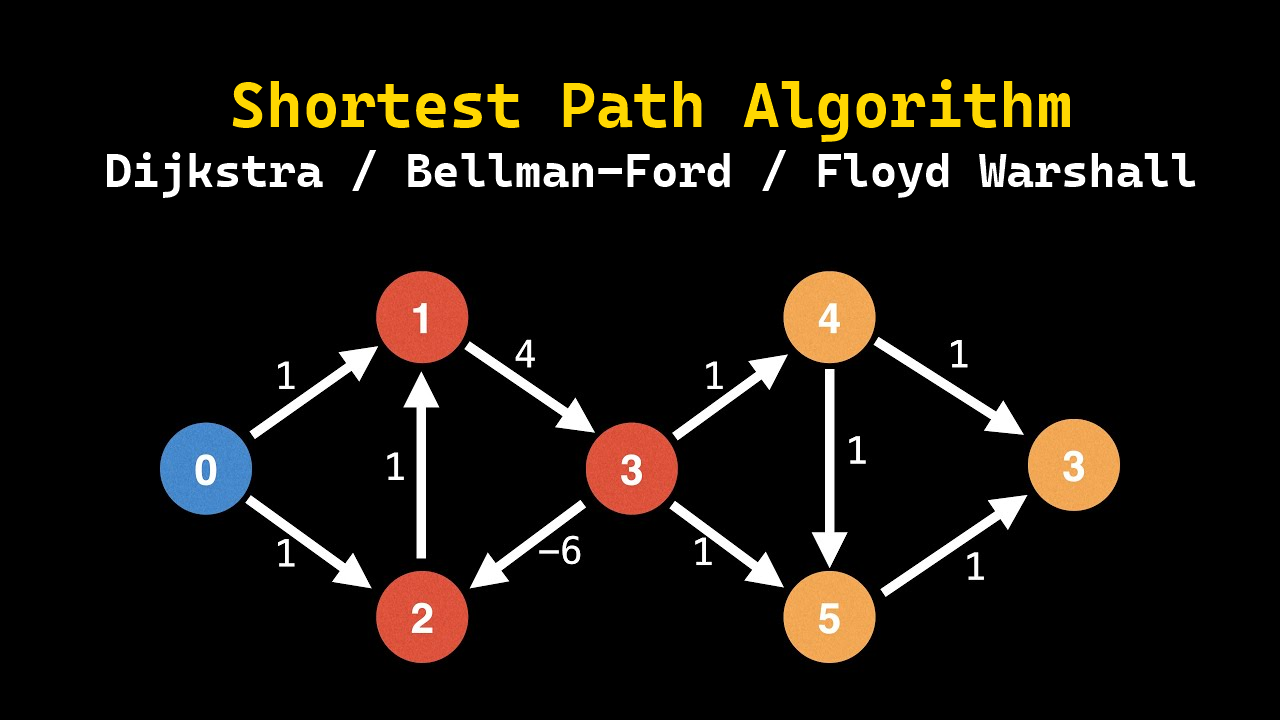
- Dijkstra Algorithm
- Bellman-Ford Algorithm
- Floyd Warshall Algorithm
-
사용 예시 ) 내비게이션과 같은 길찾기 등
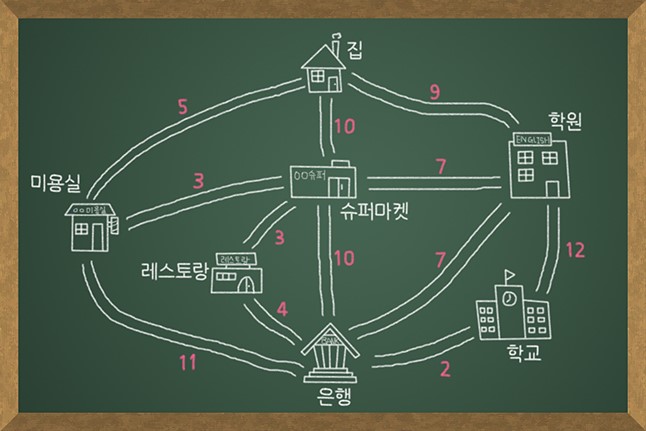
- ex) 집에서 은행까지 가는데, 어떻게 가는 길이 가장 빠를까?
01. Dijkstra Algorithm
| 특성 | Dijkstra 알고리즘 |
|---|---|
| 작동 방식 | 한 출발점 → 모든 노드까지의 최단 거리 계산 |
| 기본 아이디어 | 가장 가까운 노드부터 차례로 최단 경로 확장 |
| 그래프 유형 | 가중치가 있는 방향/무방향 그래프 (음수 가중치 X) |
| 음수 가중치/사이클 허용 여부 | 음의 가중치, 음수 사이클 불가 |
-
구체적인 작동 과정
- 출발 노드 설정
- 출발 노드를 기준으로 각 노드의 최소 비용 저장
- 방문하지 않은 노드 중에서 가장 비용이 적은 노드 선택
- 해당 노드를 거쳐 특정 노드로 가는 경우를 고려하여 최소 비용 갱신
- 위의 3~4번 과정 반복
-
ex) 아래와 같은 그래프가 있다고 가정했을 때.

-
2차원 배열 형태로 다음과 같이 초기화
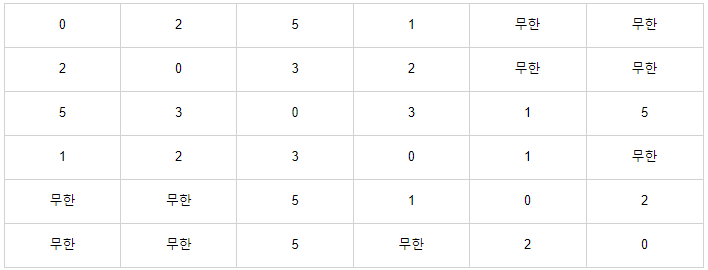
-
출발 노드 설정 ( 1번 노드로 설정 )

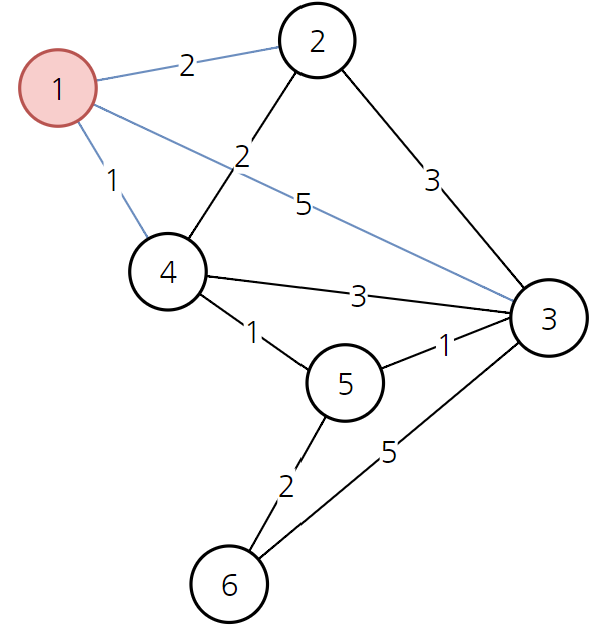
노드 1을 선택하고, 이와 연결된 세 개의 간선 확인
→ 가장 비용이 적은 노드는 '4번 노드'

→ 4번 노드를 거쳐가는 경우를 모두 고려해 최소 비용 배열 갱신:
1 → 4 → 3 = 4
1 → 4 → 5 = 2
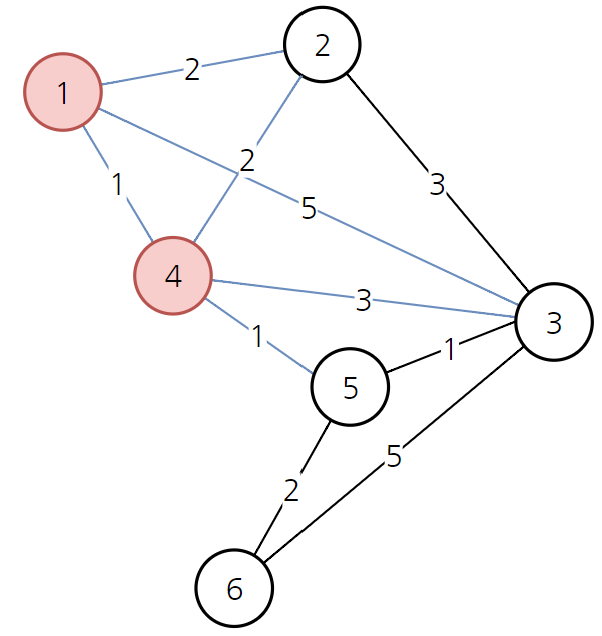
→ 다음으로 가장 비용이 적은 노드는 2번 노드

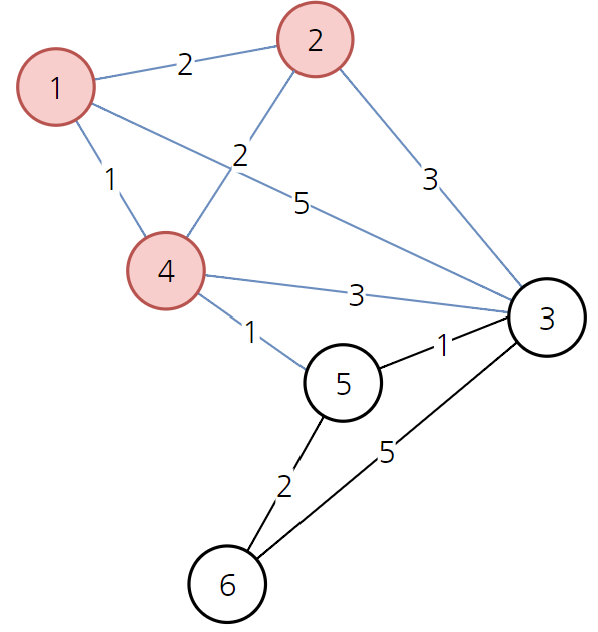
→ 2를 거쳐도 갱신되는 최소 비용이 없으므로 유지
→ 다음으로 방문하지 않은 노드 중 가장 비용이 적은 노드는 5번 노드
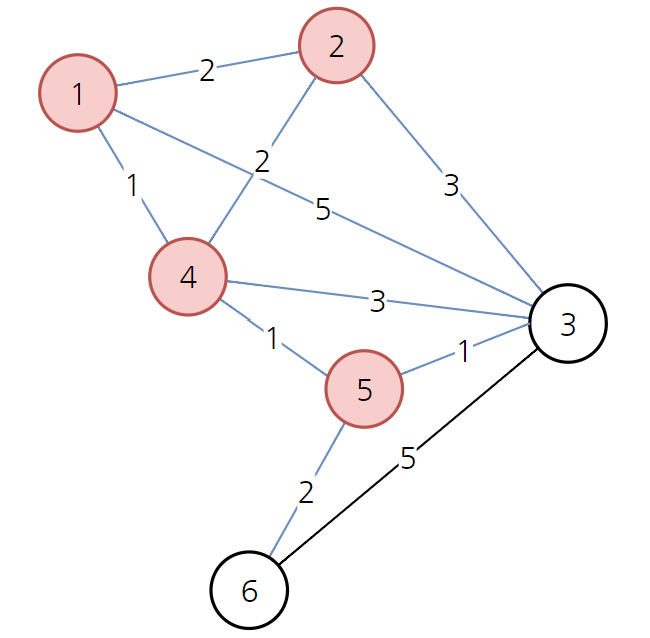
→ 5번 노드를 거쳐가는 경우를 모두 고려해 최소 비용 배열 갱신:
1 → 4 → 5 → 3 = 3
1 → 4 → 5 → 6 = 4
→ 위와 같이 남은 노드 3, 6 반복
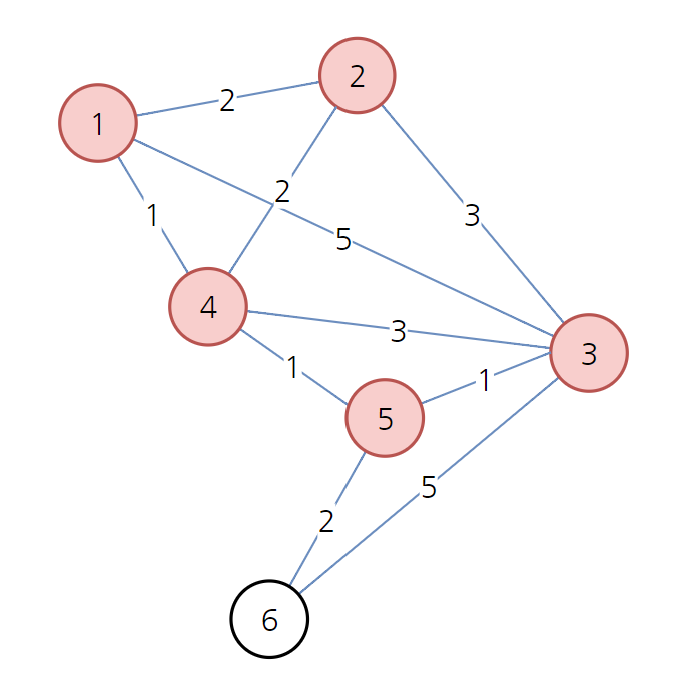

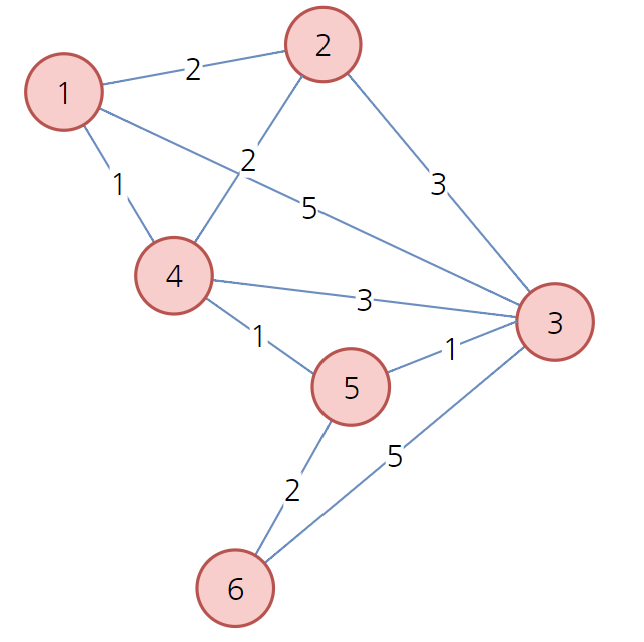

<최종 결과>
-
노드 1로부터 각 노드로 가는 최단 경로의 거리

-
02. Bellman-Ford Algorithm
| 특성 | Bellman-Ford 알고리즘 |
|---|---|
| 작동 방식 | 한 출발점 → 모든 노드까지의 최단 거리 계산 |
| 기본 아이디어 | 모든 간선을 반복적으로 탐색해 최단 거리 업데이트 |
| 그래프 유형 | 가중치가 있는 방향/무방향 그래프 (음수 가중치 O) |
| 음수 가중치/사이클 허용 여부 | 음의 가중치 허용, 음수 사이클 불가(잘못된 결과 발생 가능) |
- 구체적인 작동 과정
-
출발 노드를 설정한다.
-
최단 거리 테이블을 초기화한다.
-
다음의 과정을 V-1번 반복한다. ( V=정점의 개수)
- 모든 간선 E개를 하나씩 확인한다.
- 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
* 만약 음수 간선 순환이 발생하는지 체크하고 싶다면 3번 과정을 한 번 더 수행한다.
이 때 최단 거리 테이블이 갱신된다면 음수 간선 순환이 존재하는 것이다.
-
Dijkstra는 최단 거리 간선들을 통해 노드들을 접근하고 갱신하는데 반해, Bellman-Ford는 모든 간선들을 한 번씩 접근해 갱신한다.
관련 글 (Bllman-Ford Python 코드 포함)
99클럽 코테 스터디 29일차 TIL <Baekjoon - [Gold IV] 타임머신 - 11657>
https://velog.io/@takealittletime/99클럽-코테-스터디-29일차
03. Floyd Warshall Algorithm
| 특성 | Floyd-Warshall 알고리즘 |
|---|---|
| 작동 방식 | 모든 쌍의 노드 간 최단 경로 계산 |
| 기본 아이디어 | 모든 노드 쌍의 거리를 행렬로 관리하고 거리 업데이트 (경유지,출발지, 도착지를 나눠 출발지 → 도착지 거리와 출발지 → 경유지 → 도착지 거리 비교) |
| 그래프 유형 | 가중치가 있는 방향 그래프 (음수 가중치 O) |
| 음수 가중치/사이클 허용 여부 | 음의 가중치 허용, 음수 사이클 불가(탐색 가능) |
*플로이드 워셜 알고리즘의 핵심:
각 단계마다 경유지 k를 거쳐가는 경우를 확인한다.
점화식을 살펴보면 아래와 같다.
- ( 출발지 i → 도착지 j ) vs ( 출발지 i → 경유지 k → 도착지 j) 중 어느 것이 더 최소 비용인지 계속해서 찾는 것이다.
위의 점화식을 기반으로 코드를 작성하면 아래와 같이 3중 반복문으로 작성이 가능하다.for k in range(1, V+1): graph[k][k] = 0 for i in range(1, V+1): for j in range(1, V+1): graph[i][j] = min(graph[i][j], graph[i][k]+graph[k][j])
-
구체적인 작동과정
- 그래프의 각 정점까지의 비용을 2차원 배열 형태로 구현
- 경유지 노드를 기준으로 출발지, 도착지에 대해
계속해서 (출발지 → 도착지) VS (출발지 → 경유지 → 도착지) 비교, 더 적은 비용의 값으로 배열 업데이트.
ex) 아래와 같은 그래프가 있다고 했을 때

-
위의 그래프를 2차원 배열 형태로 표현
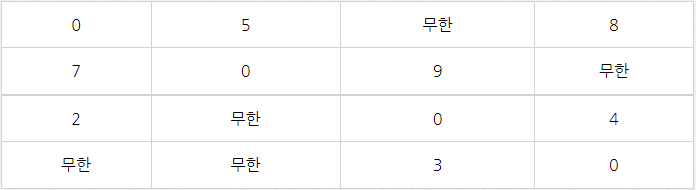
-
노드 1을 경유해 가는 경우 업데이트
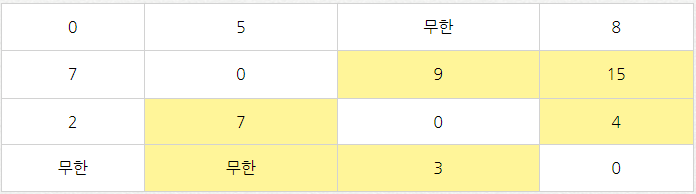
-
노드 2를 거쳐가는 경우 업데이트

-
~~노드 3, 노드 4에서도 위와 같은 방식으로 업데이트
→ 모든 쌍에 대한 최단 거리를 할당한 다음과 같은 결과 반환
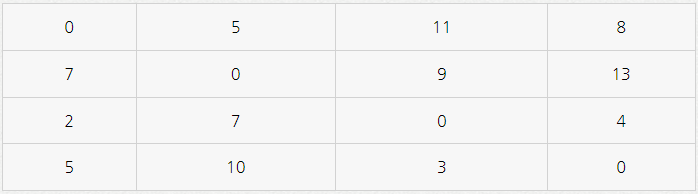
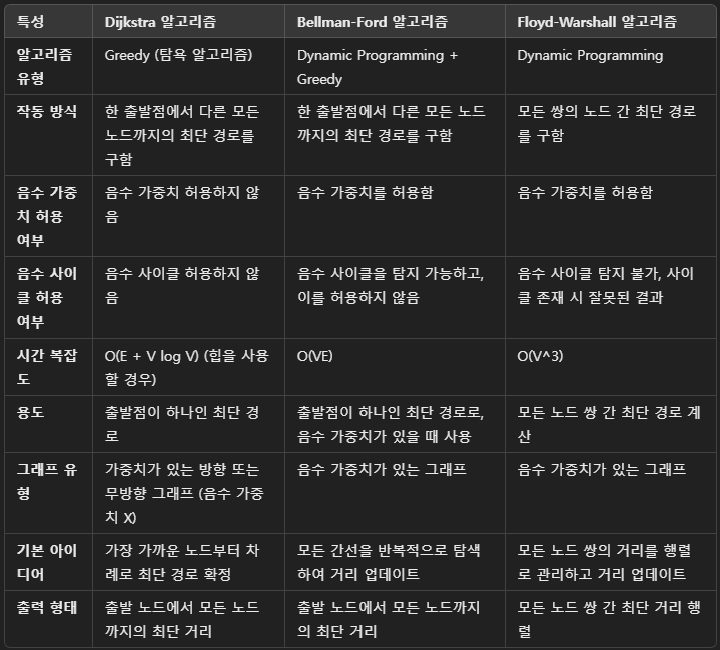
*세 가지 알고리즘의 차이 정리
참고 자료 / 이미지 출처 ::
-
최단 경로 알고리즘
https://blog.naver.com/msnayana/220312656216 -
[자료구조] 최단 거리 알고리즘 정리 (다익스트라, 벨만 포드, 플로이드 워셜)
https://roytravel.tistory.com/340 -
23.다익스트라(Dijkstra) 알고리즘
https://m.blog.naver.com/ndb796/221234424646 -
24.플로이드 와샬(Floyd Warshall) 알고리즘
https://blog.naver.com/ndb796/221234427842
Cookie. 🍪