딥러닝 기초 | 인공신경망 & 경사하강법

DNN 깊은인공신경망

신경의 생물학적 작동원리를 모방해
노드: 신호를 받는 부분 (Nin)
엣지: thresold에 따라 전달할지 말지를 정하고
커넥션: 전달한다

활성함수 Activation function

(신경이라고 치면...)자극임계값을 계산하는 함수

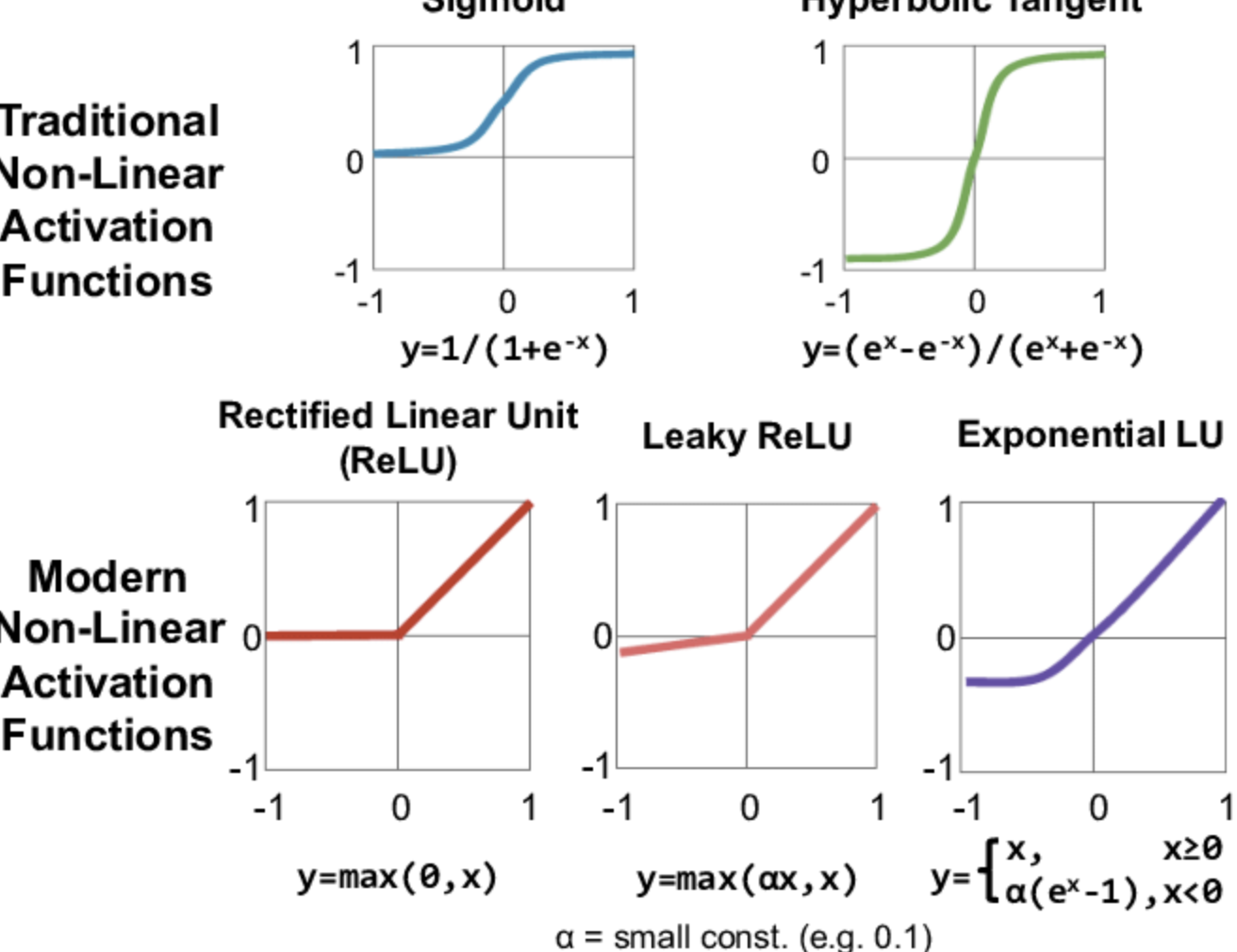
(대충 이런 어디서 많이 본 것들..)

웨이트 : 각 파라미터의 가중치
바이어스 : y 절편ㅎㅎ...

• 여기서 같은 레이어에 있는 2개 노드의 웨이트의 값이 동일하다면? => 신경망의 다양성x
  => 각 노드가 가진 웨이트 세트가 각 노드의 역할을 결정한다

로스함수:

• 완전 인공신경망의 핵심!
• 해당 파라미터가 얼마나 좋은지 안 좋은지 판단
• 이걸로 판단하고 그 내역으로 다음 스탭 결정됨
• 원래는 오차값들의 평균...이어야 하는데 -> 오차값이 양수도 있고 음수도 있다는 문제 생김-> 따라서 제곱하거나 절대값 하거나 -> 제곱을 취하면 파라미터 변화에 더 민감
• MSE Loss (Mean Squared Error Loss) : 제곱 방식
• MAE Loss (Mean Absolute Error Loss) : 절대값 방식

딥러닝 == 최적 웨이트 찾는 과정

경사하강법(Gradient Descent)

• 다음 스텝 = 이전 스텝 - (학습률 * Loss 함수의 기울기)
• 로스함수의 기울기는 로스가 많아지는 방향 그러니까 그 반대로 빼는걸 해야함
• 당연히 로컬 미니멈에 빠지는 이슈 생김