DFS(Depth-First Search)

Graph Traversal (그래프 순회)

(1)정의 :깊이 우선탐색

-하나의 경로를 끝까지 탐색한 후 도착이 아니라면 다음 경로로 넘어가는 탐색

(2) 특징

-순환알고리즘 형태를 가지고 있다.
-어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다.

(3) 과정

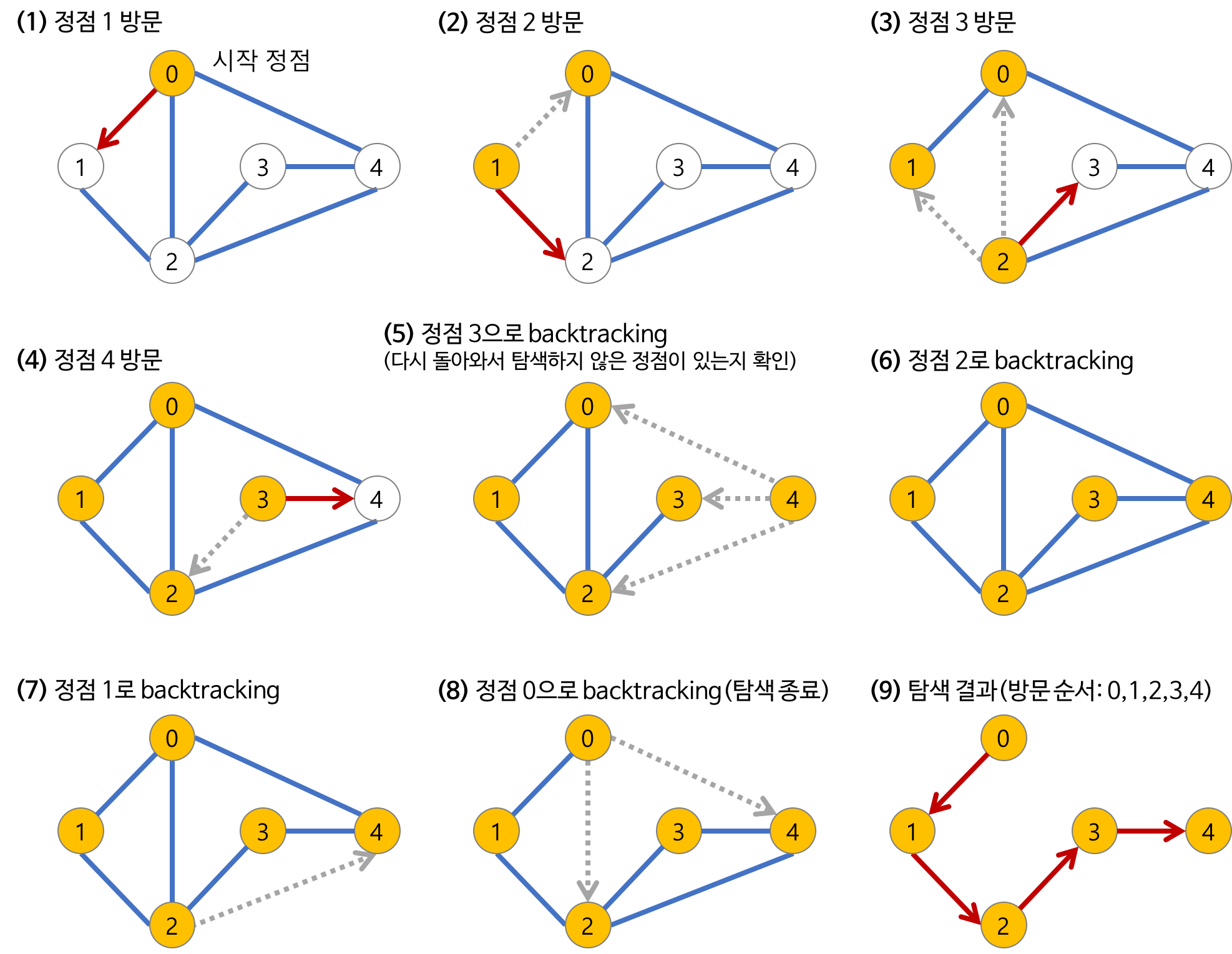
1.a 노드(시작 노드)를 방문한다.
방문한 노드는 방문했다고 표시한다.

2.a와 인접한 노드들을 차례로 순회한다.
a와 인접한 노드가 없다면 종료한다.

3.a와 이웃한 노드 b를 방문했다면, a와 인접한 또 다른 노드를 방문하기 전에 b의 이웃 노드들을 전부 방문해야 한다.
b를 시작 정점으로 DFS를 다시 시작하여 b의 이웃 노드들을 방문한다.

4.b의 분기를 전부 완벽하게 탐색했다면 다시 a에 인접한 정점들 중에서 아직 방문이 안 된 정점을 찾는다.
즉, b의 분기를 전부 완벽하게 탐색한 뒤에야 a의 다른 이웃 노드를 방문할 수 있다는 뜻이다.
아직 방문이 안 된 정점이 없으면 종료한다.
있으면 다시 그 정점을 시작 정점으로 DFS를 시작한다.

(4)시간복잡도

-그래프를 인접 행렬로 표현할 경우
for loop이 V만큼 돌기 때문에 O(V) 시간만큼 필요하고 정점을 반물할때 마다 DFS를 부르기 때문에 O(V^2)이다
(V:간선집합)

-그래프를 인접 리스트로 표현할 경우
전체 DFS가 다 끝난 이후를 생각해 보면,DFS가 다 끝났을 시점에는 모든 정점을 한번씩 방문하고, 모든 간선을 한번씩 검사하게 되므로. O(V+E)이다.
(V: 간선집합,E:노드집합)

(5)구현

  // DFS
  traverseDFS(vertex) {
    const visited = {};
    this._traverseDFS(vertex, visited);
  }
  _traverseDFS(vertex, visited) {
    visited[vertex] = true;
    console.log(`방문한 노드 : ${vertex}`);
    for (let adjacentVertex in this.edges[vertex]) {
      if (!visited[adjacentVertex]) {
        this._traverseDFS(adjacentVertex, visited);
      }
    }
  }