BFS(Breadth_First Search)

Graph Traversal (그래프 순회)

(1)정의:너비 우선탐색

-가까운 정점부터 탐색을 하고 더는 탐색할 정점이 없을 때, 그 다음에 떠어저 있는 정점을 순서대로 방문

(2)특징

-직관적이지 않은 면이 있다(시작노드에서 거리에 따라 단계별로 탐색함)
-재귀적으로 동작하지 않음
-어떤 노드를 탐색했는지 반드시 검사해야함(무한loop 빠질수 있음)
-queue 사용한다.
-prim,dijkstra 알고리즘과 유사

(3)방법

깊이가 1인 모든 노드를 방문하고 나서 그 다음에는 깊이가 2인 모든 노드를, 그 다음에는 깊이가 3인 모든 노드를 방문하는 식으로 계속 방문하다가 더 이상 방문할 곳이 없으면 탐색을 마친다.

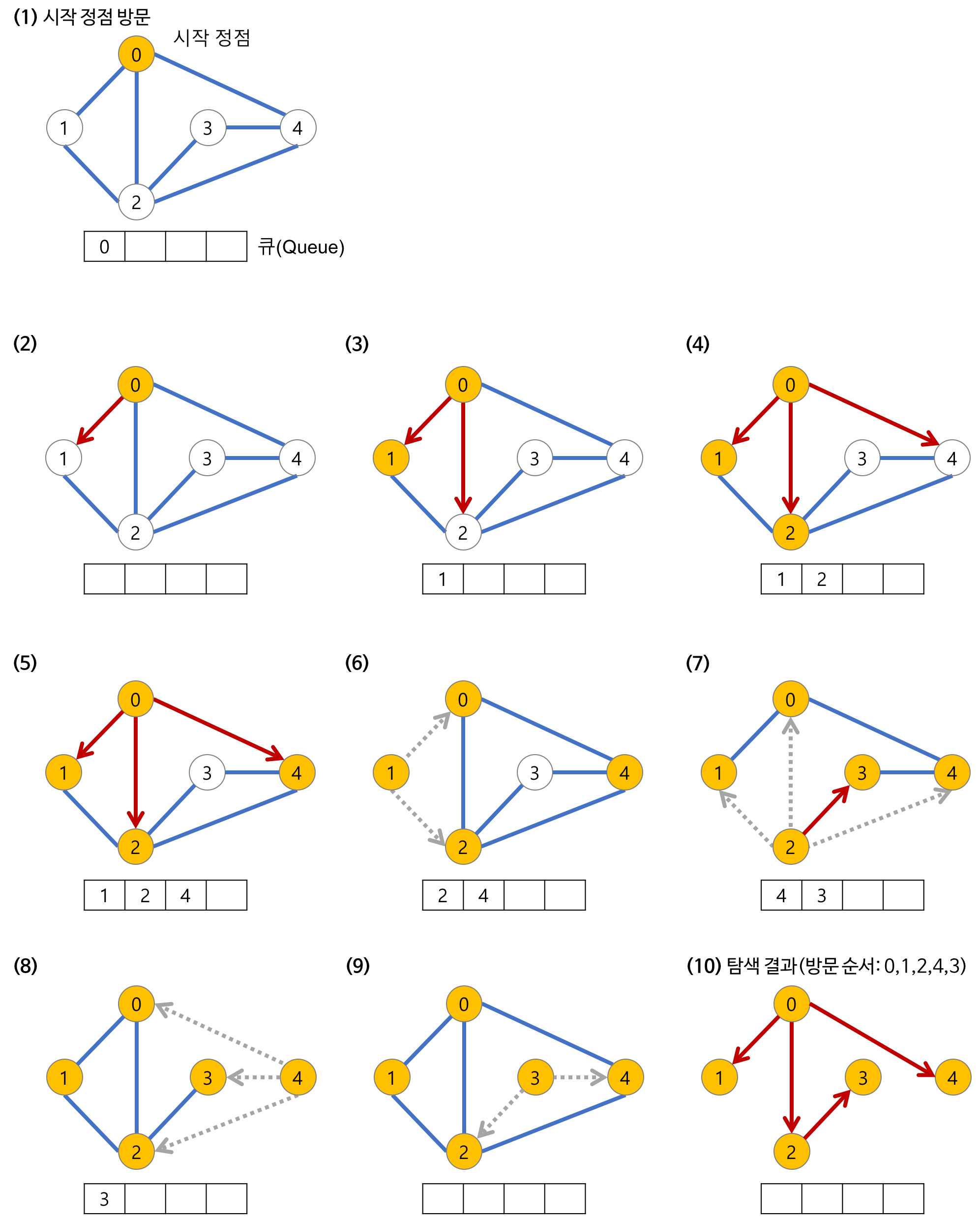
1.a 노드(시작 노드)를 방문한다. (방문한 노드 체크)
큐에 방문된 노드를 삽입(enqueue)한다.
초기 상태의 큐에는 시작 노드만이 저장
즉, a 노드의 이웃 노드를 모두 방문한 다음에 이웃의 이웃들을 방문한다.

2.큐에서 꺼낸 노드과 인접한 노드들을 모두 차례로 방문한다.
큐에서 꺼낸 노드를 방문한다.
큐에서 커낸 노드과 인접한 노드들을 모두 방문한다.
인접한 노드가 없다면 큐의 앞에서 노드를 꺼낸다(dequeue).
큐에 방문된 노드를 삽입(enqueue)한다.

3.큐가 소진될 때까지 계속한다.

(4)시간복잡도

해당 라인은 모든 간선에 대해서 한 번씩 비교할 것이기 때문에 총 E번 반복할 것이고, 각 정점을 한 번씩 모두 방문하여 V의 시간이 걸릴 것이다.따라서, 인접 리스트로 구현한 BFS의 시간 복잡도는 O(V+E) 이다.

(5)구현

function bfs(vertexList, vertex, visited) {
  // bfs -> queue
  const queue = [vertex];
  visited[vertex] = true;
  
  while(queue.length>0) {
    const cur = queue.shift();
    for(let i=0; i<vertexList[cur].length; i++) {
      if(!visited[vertexList[cur][i]]) {
        queue.push(vertexList[cur][i]);
        visited[vertexList[cur][i]] = true;
      }
    }
  }
}