Tree

1)정의

계층적 구조를 갖는 자료를 표현하기 위한 자료구조
(하나의 뿌리로부터 가지가 사방을 뻗은 형태)

2)용어

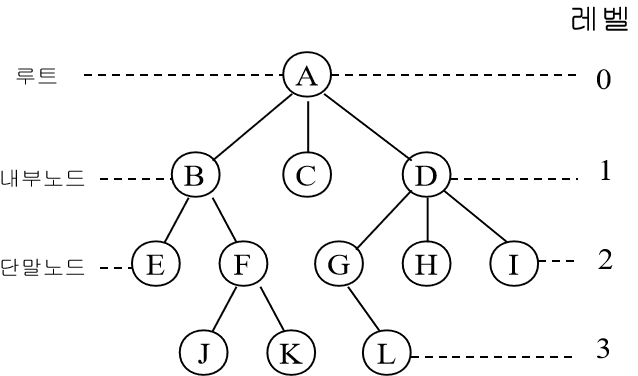
노드(Node) : 트리구조를 이루는 모든 개별 데이터
루트(Root) : 트리 구조의 시작점이 되는 노드
부모 노드(Parent node): 두 노드 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
자식 노드(Child node): 두 노드 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
리프(Leaf): 트리 구조의 끝지점이고,자식 노드가 없는 노드
깊이(depth): 루트로부터 하위 계층의 특정 노드까지의 깊이
레벨(Level): 같은 깊이를 가지고 있는 노드를 묶어서 레벨로 표현
높이(Height): 리프 노드를 기준으로 루트까지의 높이
서브트리(Sub tree): 트리구조를 갖춘 작은 트리(포함관계)

3)예시

월드컵 토너먼트, 족보,조직도 등등

4)구현

class Tree {
  constructor(value) {
		// constructor로 만든 객체는 트리의 Node가 됩니다.
    this.value = value;
    this.children = [];
  }

	// 트리의 삽입 메서드를 만듭니다.
  insertNode(value) {
    const childNode = new Tree(value);
    this.children.push(childNode);
  }

	// 트리 안에 해당 값이 포함되어 있는지 확인하는 메서드를 만듭니다.
  contains(value) { 
     if(this.value === value){
       return true;
     }
	   for(let i =0;i<this.children.length;i++){
      const childNode = this.children[i];
      if(childNode.contains(value)){
        return true;
      }
    }
		// 전부 탐색했음에도 불구하고 찾지 못했다면 false를 반환합니다.
    return false;
  }
}

5)BST(Birary Search Tree)

(1)정의

각 노드가 왼쪽과 오른쪽 최대2개를 갖는 트리구조

(2)종류

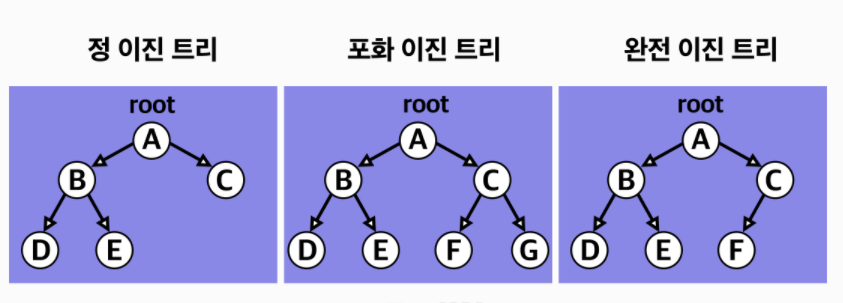
정 이진 트리(Full Binary Tree) : 각 노드가 0개혹은 2개의 자식노드를 갖는 트리
포화 이진트리(Perfect binary tree):모든 리프 노드의 레벨이 동일하고 모든 레벨이 가득 채워져 있는 트리
완전 이진트리(Complete binary tree): 마지막 레벨을 제외한 모든 노드가 가득차있고 마지막 레벨 노드가 전부 차있지 않않아도 되지만 왼쪽이 채워져야 하는 트리

(3)특징

모든 왼쪽 자식의 값이 루트나 부모보다 작고 머든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가진다

(4)Tree traversal

전위순회: 루트->왼쪽노드 ->오른쪽 노드 순으로 순회
중위순회: 왼쪽노드 ->루트->오른쪽 노드 순으로 순회
후위순회:왼쪽노드 ->오른쪽노드 ->루트 순으로 순회

(5) 구현

class BinarySearchTree {
  constructor(value) {
		// constructor로 만든 객체는 이진 탐색 트리의 Node가 됩니다.
    this.value = value;
    this.left = null;
    this.right = null;
  }
	// 이진 탐색 트리의 삽입하는 메서드를 만듭니다.
  insert(value) {
		// 입력값을 기준으로, 현재 노드의 값보다 크거나 작은 것에 대한 조건문이 있어야 합니다.
		// 보다 작다면, Node의 왼쪽이 비어 있는지 확인 후 값을 넣습니다.
    
    if (value < this.value) {
      if (this.left === null) {
        this.left = new BinarySearchTree(value);
      } else {.
        this.left.insert(value);
      }    
		// 보다 크다면, Node의 오른쪽이 비어 있는지 확인 후 값을 넣습니다.
    } else if (value > this.value) {
      if (this.right === null) {
        this.right = new BinarySearchTree(value);
      } else {
        this.right.insert(value);
      }
		//그것도 아니라면, 입력값이 트리에 들어 있는 경우입니다.
    } else {
      // 아무것도 하지 않습니다.
    }
  }

	// 이진 탐색 트리 안에 해당 값이 포함되어 있는지 확인하는 메서드를 만듭니다.
  contains(value) {
    if (this.value === value) {
      return true;
    }
		// 입력값을 기준으로 현재 노드의 값보다 작은지 판별하는 조건문이 있어야 합니다.
    if (value < this.value) {
	   if(this.left !== null && this.left.contains(value)){
        return true;
       }else{
         return false;
       } 
    }
		// 입력값을 기준으로 현재 노드의 값보다 큰지 판별하는 조건문이 있어야 합니다.
    if (value > this.value) {                                			     
     if(this.right !== null && this.right.contains(value)){
        return true;
       }else{
         return false;
       }
    }
		// 없다면 false를 반환합니다.
    return false;
  }

	// 이진 탐색 트리를 전위 순회하는 메서드를 만듭니다.
  preorder(callback) {
		callback(this.value);
    if (this.left) {
      this.left.preorder(callback);
    };
    if (this.right) {
      this.right.preorder(callback);
    };
  }

	// 이진 탐색 트리를 중위 순회하는 메서드를 만듭니다.
  inorder(callback) {
   if (this.left) {
      this.left.inorder(callback);
    };
    callback(this.value);
    if (this.right) {
      this.right.inorder(callback);
    };
  }

	// 이진 탐색 트리를 후위 순회하는 메서드를 만듭니다.
  postorder(callback) {
		//TODO: 전위 순회를 바탕으로 후위 순회를 구현하세요.
     if (this.left) {
      this.left.postorder(callback);
    };
    if (this.right) {
      this.right.postorder(callback);
    };
    callback(this.value);
  }

}