Dynamic Programming (동적 계획법)

주어진 문제를 여러 개의 하위 문제로 나누어 풀고, 하위 문제들의 해결 방법을 결합하여 최종 문제를 해결하는 문제 해결 방식을 말합니다.

조건

• 큰 문제를 작은 문제로 나눌 수 있고, 작은 문제가 중복해서 발견된다 (Overlapping Sub-problems)
• 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 같다. 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다.(Optimal Substructure)

예시

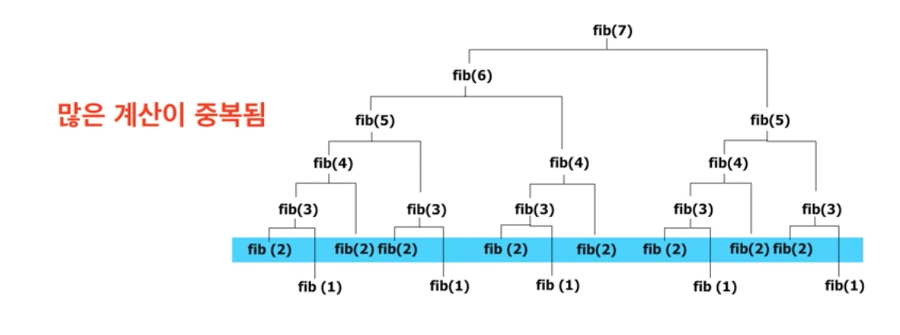
기존의 피보나치 함수의 답을 구할려고했다면 이렇게 작성했을 테지만,

function fibo(n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    return fibo(n - 1) + fibo(n - 2);
}

중복되는 값을을 매번 일일히 계산함으로 시간복잡도가 증가합니다. 이 경우에 시간 복잡도는 O(n^2) 입니다.
이 중복을 제거하기 위해서 메모이제이션(Memoization)이라는 테크닉을 사용합니다.

function fibo(n) {
    memo = [0, 1];
    for (let i = 0; i <= n; i++) 
        memo[i] = memo[i - 1] + memo[i - 2];
    return memo[n];
}

계산한 값을 배열해 저장해서 재활용합니다.

방법

Dynamic Programming 에는 2가지 방법이 있습니다.

• Top-Down 방식 : 하향식 방법, 가장 큰 문제를 방문하고 작은 문제를 호출하며 답을 찾는 방식 (Memoization + recursive)

function fibMemo(n, memo = []) {
		// 이미 해결한 하위 문제인지 찾아본다
    if(memo[n] !== undefined) {
      return memo[n];
    }
    if(n <= 2) {
      return 1;
    }
		// 없다면 재귀로 결괏값을 도출하여 res 에 할당
    let res = fibMemo(n-1, memo) + fibMemo(n-2, memo);
		// 추후 동일한 문제를 만났을 때 사용하기 위해 리턴 전에 memo 에 저장
    memo[n] = res;
    return res;
}

• Bottom-Up 방식 : 상향식 방법으로, 작은 문제들로 답을 구해가며 전체 문제의 답을 찾는 방식입니다.(Itertaion + Tabulation)

function fibTab(n) {
    if(n <= 2) {
    	return 1;
    }
    let fibNum = [0, 1, 1];
    for(let i = 3; i <= n; i++) {
        fibNum[i] = fibNum[i-1] + fibNum[i-2];
		// n >= 3 부터는 앞서 배열에 저장해 놓은 값들을 이용하여
		// n번째 피보나치 수를 구한 뒤 배열에 저장 후 리턴한다 
    }
    return fibNum[n];
}

예시

coinChange

• naive : O(2^M * N)

const coinChange = function (total, coins) {
	const makeChange = (left, idx) => {
    	if (total === 0) { return 1};
      	else {
        let cnt = 0;
          for (let i = idx; i < coins.length; i++) {
          	cnt = cnt + makeChange(left - coins[i], i);
          }
        }
      return cnt;
    } //left에는 total 값이 들어갑니다.
}return makeChange(total, 0);

coinChange가 결국 return 하는 값은 cnt = cnt + cnt + cnt...1 입니다.

• simple recursion and dp with memoization: O(M * N)

const coinChange = function (total, coins) {
	const memo = [] // memoization 기록할 곳
    for (let i = 0; i < total +1; i++) {
    	memo.push(Array(coins.length).fill(-1))
    } // -1로 채운 coins 수만큼 배열을 memo에 만듭니다
  	const makeChange = (left, idx) => {
    if (left === 0) { return 1} ; // 필요충족조건에 도달했을 때!
    else if (left < 0) { return 0 } ; // total 금액보다 더 많이 빼버린 경우, 조건을 충족하지못해서 횟수로 계산하지않습니다.
   else if (idx >= coins.length && left > 0) return 0 // toal 금액보다 모지란 경우 역시도, 조건을 충족하지못했기 때문에 횟수로 인정하지않습니다.
    }
    else if (memo[left][idx] !== -1) { return memo[left][idx]};
  // 해결하지못한 문제는 다시 풀지 않습니다.
	memo[left][idx] = makeChange(left, idx+1) + makeChange(left - coins[idx], idx);
	}
return makeChange(total, 0)
}

• dynamic programming with tabulation: O(M * N) (bottom up)

const coinChange = function (total, coins) {
	const table = []
    for (let i = 0; i < total+1; i++) {
    	table.push(Array(coins.length).fill(0))
    }
  	for (let i = 0; i < coins.length; i++) {
    	table[0][i] = 1;
    }
  	for (let amount = 1; amount <= total; amount++) {
    	for (let idx = 0; idx < coins.length; i++) {
        let coinInclude = 0;
          if (amount - coins[idx] >= 0) {
          	coinInclude = table[amount - coins[idx]][idx];
          }
          let coinExclude = 0;
          if (idx >= 1) {
          	coinExclude = table[amount][idx -1];
          }
          table[amount][idx] = coinInclude + coinExclude
        }
    }
  return table[total][coins.length -1]
}